Задание №16 на ЕГЭ по информатике. Использование рекурсивных алгоритмов

Алгоритм называется рекурсивным, если в его определении содержится прямой или косвенный вызов этого же алгоритма;
Рекурсивная функция – это такая функция, которая в процессе выполнения обращается сама к себе (зависит сама от себя).

Классические примеры рекурсивных алгоритмов.

Пример 1.
Вычисление факториала. С одной стороны, факториал определяется так: n!\(=1\cdot 2\cdot 3\cdot... \cdot (n-1) \cdot n\). С другой стороны, \(n!=(n-1)!\cdot n\), т.е. чтобы вычислить факториал числа n, нужно сначала вычислить факториал числа (n-1). Мы видим, что алгоритм вычисления факториала зависит от самого себя.
Одна из самых больших опасностей рекурсии – бесконечный вызов функцией самой себя. Если неверно построить алгоритм, то функция может пропустить конечное условие и выполняться бесконечно. Проще всего допустить эту ошибку, если не указать условие остановки. В нашем случае конечное условие – это 1!=1.

Пример 2.
Нахождение НОД (наибольшего общего делителя) двух натуральных чисел.
Есть несколько способов нахождения этого значения. Одним из них является алгоритм Евклида.Пусть есть два целыхчисла а и b.
Если а=b, то НОД(а,b)=а – конечное условие рекурсии.
Если а>b, то НОД(а,b)=НОД(а-b,b).
Если а<b, то НОД(а,b)=НОД(а,b-а). И снова мы видим, что алгоритм вычисления наибольшего общего делителя зависит сам от себя.

Таким образом, для того, чтобы задать рекурсивную функцию, нужно определить:

• условие окончания рекурсии, то есть значения параметров функции, для которых значение функции известно или вычисляется без рекурсивных вызовов;
• рекуррентную формулу (или формулы), с помощью которых значение функции для заданных значений параметров вычисляется через значение функции для других значений параметров.

Данное задание может быть решено тремя способами:

• аналитически,
• с использованием электронных таблиц
• с помощью программы на языке программирования.

Примеры решения задач

Пример 3.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(1) = 1 F(n) = 5*F(n–1) + 3*n, при n >1
Чему равно значение функции F(4)?
Решение:
Аналитический способ:
F(1) = 1
F(2)=5*F(1)+3*2=11
F(3)=5*F(2)+3*3=64
F(4)= 5*F(3)+3*4=332
Ответ: 332.

Пример 4.
Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 0
F(n) = F(n–1) + n, при n >1
G(1) = 1
G(n) = G(n–1) * n, при n >1
Чему равно значение функции F(5) + G(5)?
Решение:
С помощью программы на языке Python:
1. Для программной реализации данной задачи воспользуемся динамическим программированием, которое позволяет свести вычисление значения функции, заданной рекурсивно, к заполнению массива (таблицы)
2.
f=[0]*10 – заполняем массив f десятью нулями
g=[1]*10 – заполняем массив d десятью единицами
for n in range(2,10):
f[n] = f[n-1]+n
g[n] = g[n-1]*n
print (f[5]+g[5])
Ответ: 134

Пример 5.
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = 1, при n = 1;
F(n) = F(n-3)*n, при n > 1 чётном
F(n) = F(n-2)*n, при n > 1 нечётном
Чему равно значение выражения F(6115)/F(6112)?
Ответ округлите до целого.
Решение:
Аналитический способ:
1. В данном задании удобно выполнить обратный расчет для функции F
F(6115) = 6115*F(6113) = 6115*6113*F(6111) = 6115*6113*6111*F(6109)
F(6112) = 6112*F(6109)
2. F(6115)/F(6112) = 6115*6113*6111*F(6109)/(6112*F(6109) одинаковый множитель можно сократить посчитать числовые значения с учетом округления до целого. Получим F(6115)/F(6112) = 6115*6113*6111/6112
Ответ: 37374879

Пример 6.
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = 1, если n < 4 F(n) = n, если n > 3 и число n нечётное,
F(n) = F(n – 1) + F(n – 2) + F(n – 3), если n > 3 и число n чётное.
Чему равно значение выражения F(2254) – F(2252)?
Решение:
С помощью электронных таблиц:
1. В столбце А задаем значения n от 1 до 2254.
2. В столбце B задаем функцию: F(1)=1, F(2)=1, F(3)=1 , далее использую внешнюю функцию ЕСЛИ и внутреннюю ЕНЕЧЕТ задаем условие задачи.

3. Теперь протягиваем формулу до n=2254 и в любой ячейке, находящейся рядом посчитать значение F(2254) – F(2252). Получим 4504

Ответ: 4504

Пример 7.
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = 1 при n = 1
F(n) = 2•F(n–1) + n + 3, если n> 1
Чему равно значение функции F(19)?
Решение:
С помощью программы на языке Python:
1. Для реализации задачи воспользуемся классической реализацией рекурсивной функции. Главная проблема – не получить бесконечную рекурсию; для этого рекомендуется сразу в начале функции записать условие окончания рекурсии, которое задаётся условием «F(n) = 1 при n = 1», и сразу завершить выполнение функции.
2. Недостаток данной реализации в том, что при больших значениях аргумента функция F(n) может вычисляться очень долго.

def F( n ):
if n == 1: return 1
if n >1:
return 2*F(n-1) + n + 3
print( F(19) )
Ответ: 1834984

Пример 8.
Задача 1. Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = n, при n < 4; F(n) = F(n-3)*3, при n > 3 кратном трём;
F(n) = F(n-1)+n, при n > 3, которое даёт остаток 1 при делении на 3;
F(n) = F(n-2)+n, при n > 3, которое даёт остаток 2 при делении на 3.
Чему равно значение выражения F(7000) - 9 * F(6993)?
Решение:
Аналитический способ:
1. Будем выполнять обратный расчет функции F.Т.к 7000 при делении на 3 дает остаток 1 можно записать F(7000) = F(6999) +7000
2. Число 6999 кратно 3, поэтому
F(6999) = (6993)*3; тогда
F(7000) = 7000+ F(6996)*3 = 7000+F(6993)*3*3= 7000+9*F(6993)
3. Таким образом, F(7000) - 9 * F(6993)= 7000+9*F(6993) -9*F(6993) = 7000
Ответ: 7000

Пример 9.
Последовательность чисел трибоначчи задается рекуррентным соотношением:
F(1) = 0
F(2) = 1
F(3) = 1
F(n) = F(n–3) + F(n–2) + F(n–1), при n >3, где n – натуральное число.
Чему равно одиннадцатое число в последовательности трибоначчи?
В ответе запишите только натуральное число.
Решение:
С помощью программы на языке Python:
f=[0]*20
f[1]=0
f[2]=1
f[3]=1
for n in range(4,20):
f[n] = f[n-1]+f[n-2]+f[n-3]
print (f[11])
Ответ: 149

Пример 10.
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(1) = 1
\(F(n)=F(n-1)+2^{n-1}\), если n > 1.
Чему равно значение функции F(10)?
В ответе запишите только натуральное число.
Решение:
Аналитический способ:
F(2) = F(1) +21 = 1 + 2 =3F(3) = F(2) + 22 = 3 + 4 = 7;
F(4) = F(3) +23 = 7 + 8 = 15 F(5) = F(4) +24 = 15 + 16 = 31;
F(6) = F(5) +25 = 31 + 32 = 63F(7) = F(6) +26 = 63 + 64 = 127;
F(8) = F(7) +27 = 127 + 128 = 255 F(9) = F(8) + 28 = 255 + 256 = 511;
F(10) = F(9) + 29 = 511 + 512 = 1023
Можно заметить, что \(F(n)=2^n-1\).
Ответ: 1023

Пример 11
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = 1, если n < 3 F(n) = F(n – 1) + F(n – 2), если n > 2.
Чему равно значение выражения (F(1006) – F(1004)) / F(1005)?
Решение:
С помощью электронных таблиц:
1. В столбце А задаем значения n от 1 до 1006.
2. В столбце B задаем функцию: F(1)=1, F(2)=1, F(3)=F(1)+F(2), далее протягиваем формулу до строки 1006 .

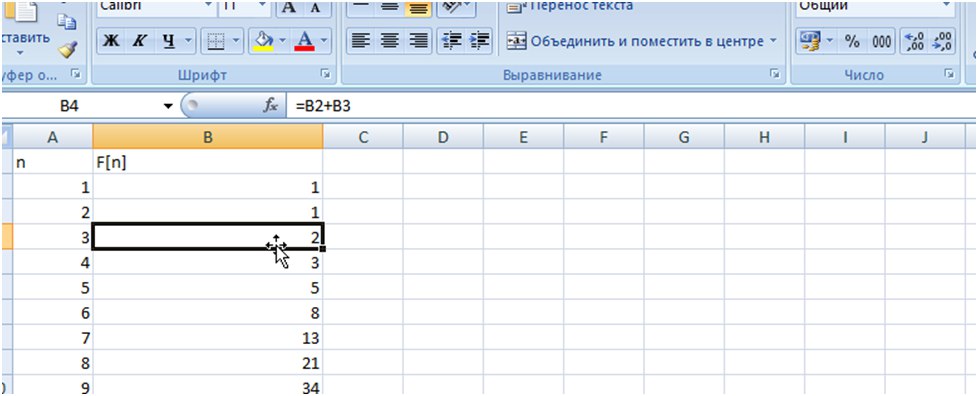
3. Далее в отдельной ячейке считаем искомое выражение.
4. Примечание: В электронных таблицах большие числа представляются в виде чисел с плавающей точкой.Например, значение в ячейке 7Е+204 означает \(7*10^{204}\). Видим, что значения очень большие.
5. Еще одно примечание: самое большое число, которое можно записать в Excel примерно равно \(10^{308}\).

Ответ: 1

Пример 12.
Алгоритм вычисления значения функции F(n). где n - натуральное число, задан следующими соотношениями:
F(1)= 1; F(2)=1;
F(n) = 2*F(n-2) + n при n >2.
Чему равно значение функции F(15)? В ответе запишите только натуральное число.
Решение6
С помощью программы на языке Python:
def F(n):
if n == 1:
return 1
if n == 2:
return 1
if n > 2:
return 2*F(n-2) + n
print(F(15))

Ответ: 749

Пример 13.
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = 1, если n = 1

\(F(n)=(2\cdot n-1)\cdot F(n-1)\), если n > 1.
Чему равно значение выражения F(316) / 631*F(313)?
Решение:
Аналитический способ:
F(316)=(316*2-1)*F(315) = (316*2-1)(315*2-1)*F(314)= (316*2-1)(315*2-1)*(314*2-1)*F(313)= = 631*629*627*F(313)
F(316) / 631*F(313)= 631*629*627*F(313) / 631*F(313)= 394383
Ответ: 394383.

Пример 14.
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = 1, если n < 3 F(n) = F(n – 1) + n – 1, если n > 2 и число n чётное,
F(n) = F(n – 2) + 2n - 2, если n > 2 и число n нечётное.
Определите значение F(34).
Решение:
С помощью электронных таблиц:
1. В столбце А задаем значения n от 1 до 34.
2. В столбце B задаем функцию: F(1)=1, F(2)=1, далее использую внешнюю функцию ЕСЛИ и внутреннюю ЕНЕЧЕТ задаем условие задачи.

3. Теперь протягиваем формулу до n=34и получим 578
Ответ: 578

Пример 15.
Функция F(n), где n - натуральное число, вычисляется по следующему правилу:
F(n) = n, если n <\(2\) F(n) = F(n / 2) + 1, если \(n \geq 2\) и число n чётное, F(n) = F(3n + 1) + 1, если \(n \geq 2\) и число n нечётное. Определите количество значений n на отрезке [1;100000], для которых F(n) равно 16. Решение: С помощью программы на языке Python: 1. Описываем функцию: при n=1 функция равна 1, при n=2, функция равна 2,далее в зависимости от четности n описываем функцию. 2. Далее задаем условие для поиска n, значение функции, в которых равно 16 и в указанном диапазоне. def F(n): if n == 1: return 1 if n == 2: return 2 if n % 2 == 0 and \(n>2\):
return F(n / 2)+1
else:
return F(3*n +1)+1
i = 1
while F(i) != 16 and i<100000: i += 1 print(i) Ответ: 22