Задание №18 ЕГЭ по информатике проверяет наше умение работать с электронными таблицами для обработки целочисленных данных. Это задание относится к категории повышенной сложности, где нужно не только понимать алгоритм, но и уметь применять его на практике.
Задача основана на работе с роботом-сборщиком монет, который перемещается по полю, представленному в виде электронной таблицы. Алгоритм движения робота задается в условии, и ключевая цель – преобразовать данные из таблицы, выполнить необходимые вычисления и ответить на вопрос задачи.
Этот тип задания проверяет не только понимание алгоритмов, но и умение логически мыслить, анализировать данные и работать с формулами в электронных таблицах. Успешное решение требует точного понимания условий задачи и последовательного выполнения операций.
Следуя правильному алгоритму и анализируя данные, вы легко справитесь с этой задачей!
Давайте ближе познакомимся с Excel и изучим формулы, которые пригодятся для успешного выполнения этого задания.
Интерфейс Excel выглядит как таблица с верхней панелью инструментов, где собраны различные функции и настройки.
Для начала важно понять, как работать с самой таблицей. Одно из базовых действий — это ввод данных в отдельные ячейки.
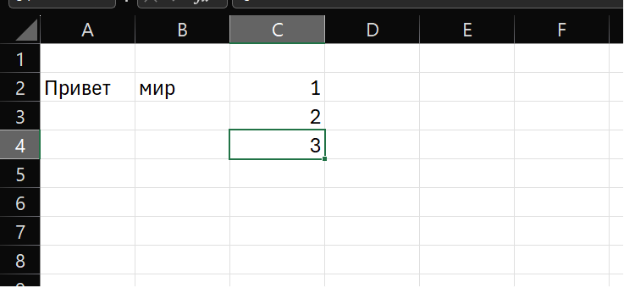
В этом примере в ячейку B2 было введено слово "мир", а в ячейку C4 — число 3. Навык определения координат ячеек играет важную роль при выполнении задач.
Одним из основных инструментов, который вы будете часто использовать в Excel, является знак равенства.
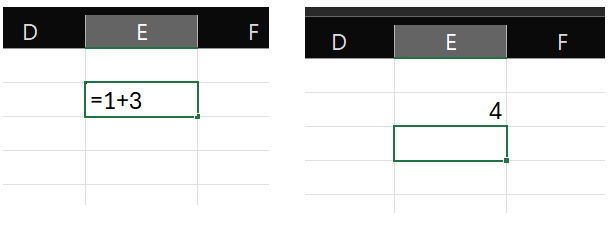
В примере выше мы использовали знак равно, а затем добавили простое арифметическое выражение. Однако возможности этого символа на этом не заканчиваются.
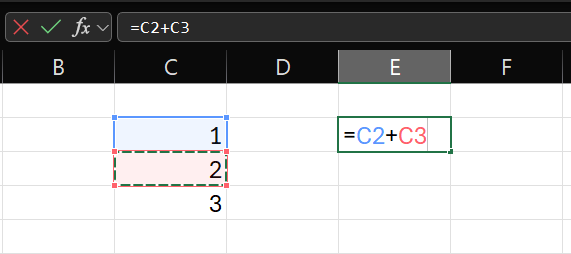
Мы можем ссылаться на другие ячейки, указывая их координаты или просто щелкая на нужную ячейку.
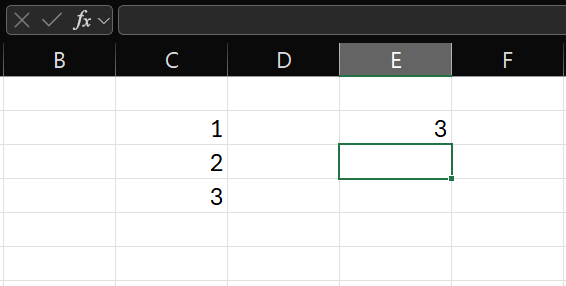
Еще один важный элемент при решении задач — это использование функций.
Как вызвать функцию:
1. Напишите знак "=" и введите название функции, затем в скобках укажите необходимые аргументы. После нажатия Enter результат функции появится в ячейке.
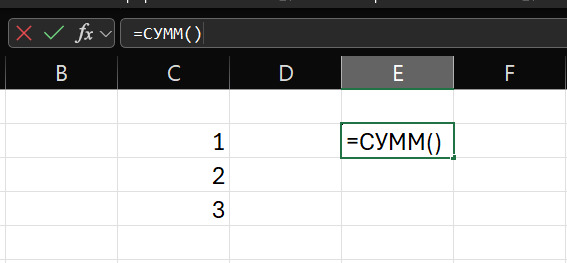
2. Вы нажимаете на кнопку функций
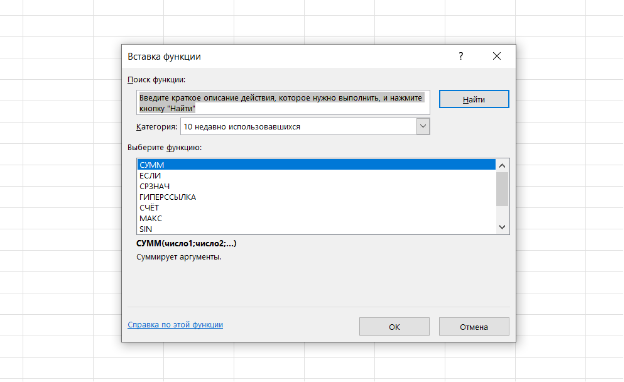
И ищете нужную вам функцию
Функций в Excel очень много и все они уникальны, но для решения 9го задания ЕГЭ по информатике нам нужны будут всего несколько:
1) Функция =СУММ() – суммирует все выделенные числа;
2) Функции =МАКС() и =МИН() находят максимальный и минимальный элемент соответственно;
3) Функция =СЧЁТЕСЛИ() в Excel подсчитывает количество ячеек, соответствующих заданному условию;
4) =ЕСЛИ() проверяет, выполняются ли заданные условия в выбранном диапазоне таблицы;
5) =НАИБОЛЬШИЙ() и =НАИМЕНЬШИЙ() — формулы для нахождения наибольшего и наименьшего значений в Excel. В этой формуле мы указываем диапазон и аргумент, который означает, «позицию в рейтинге» самых больших (маленьких) чисел.
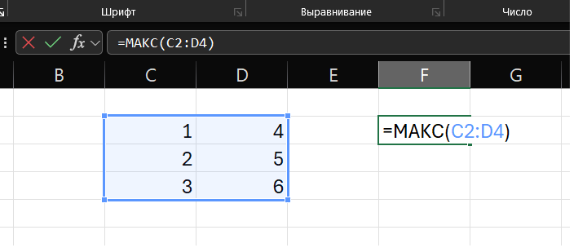
Следует также отметить, что можно выделять сразу несколько ячеек, вместо того чтобы щелкать по каждой отдельно.
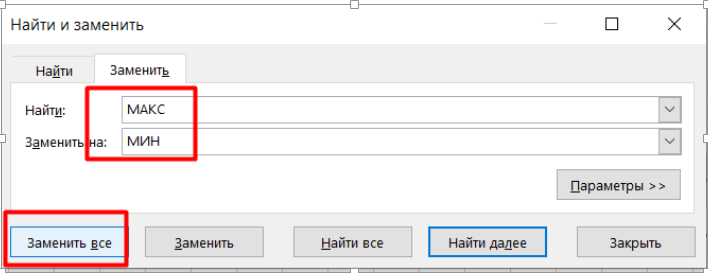
Также для решения 18го задания ЕГЭ по информатике нам понадобится инструмент «Найти и заменить»: он позволяет быстро находить и заменять данные в таблице. С его помощью можно, например:
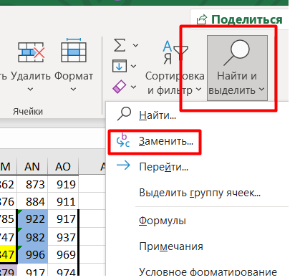
Чтобы использовать этот инструмент, нужно в правом верхнем углу выбрать «Найти и выделить», затем нажать на «заменить»:
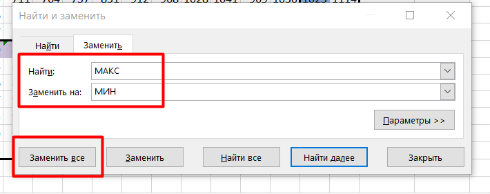
В открывшемся окне в первой строке мы пишем, что хотим найти, во второй – на что хотим заменить (в нашей задаче чаще всего мы будем искать «МАКС» и заменять на «МИН»):
Перейдём к примеру решения прототипов задач:
Разберём задачу №12 ЕГЭ 2025 из демоверсии ФИПИ:
Квадрат разлинован на N x N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. В «угловых» клетках поля — тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля.
При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута.
В ответе укажите два числа: сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N x N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
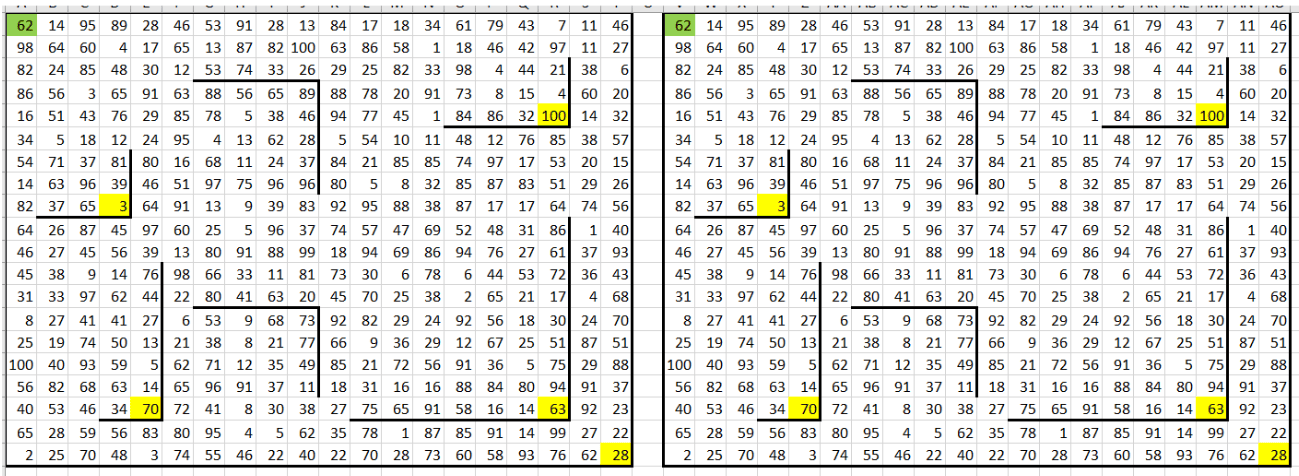
1. Открываем файл из нашего задания, анализируем условие: нам нужно найти максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута, то есть в ту клетку, которая справа и снизу ограничена стенами, давайте выделим эти ячейки жёлтым цветом, а начальную – зелёным (для того, чтобы лучше ориентироваться в таблице):
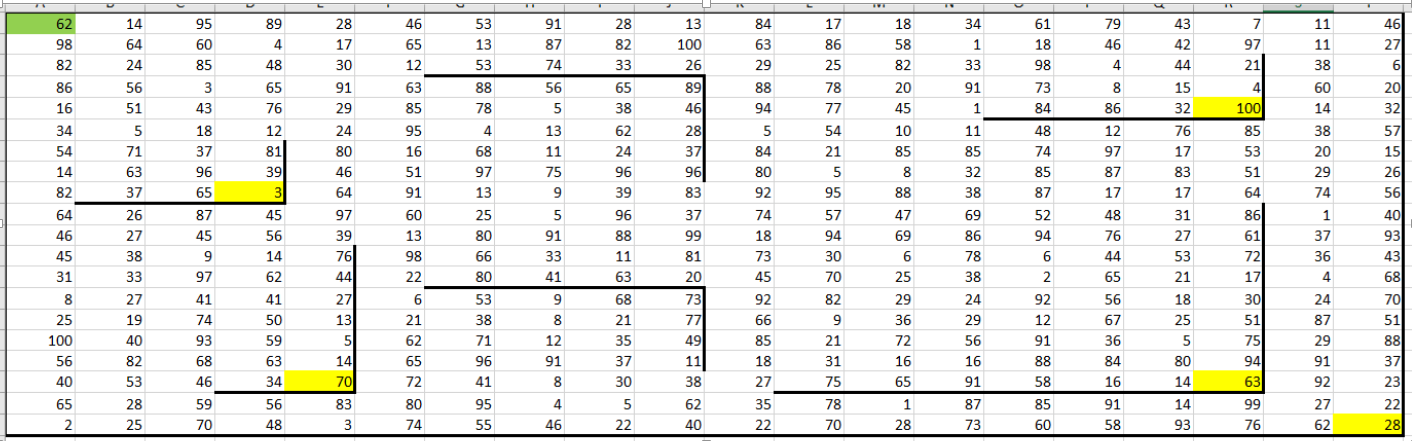
2. Создаем дополнительную таблицу: копируем поле размером 20 × 20 и вставляем его в соседний диапазон справа. Это будет наша вспомогательная таблица, в которой мы будем выполнять расчеты для определения максимальных и минимальных сумм.
3. Очищаем значения в вспомогательной таблице: мы удаляем значения монет в ячейках вспомогательной таблицы (выделяем нужный диапазон и нажимаем Delete на клавиатуре), так как эти ячейки будут заполняться формулами для выполнения расчетов.
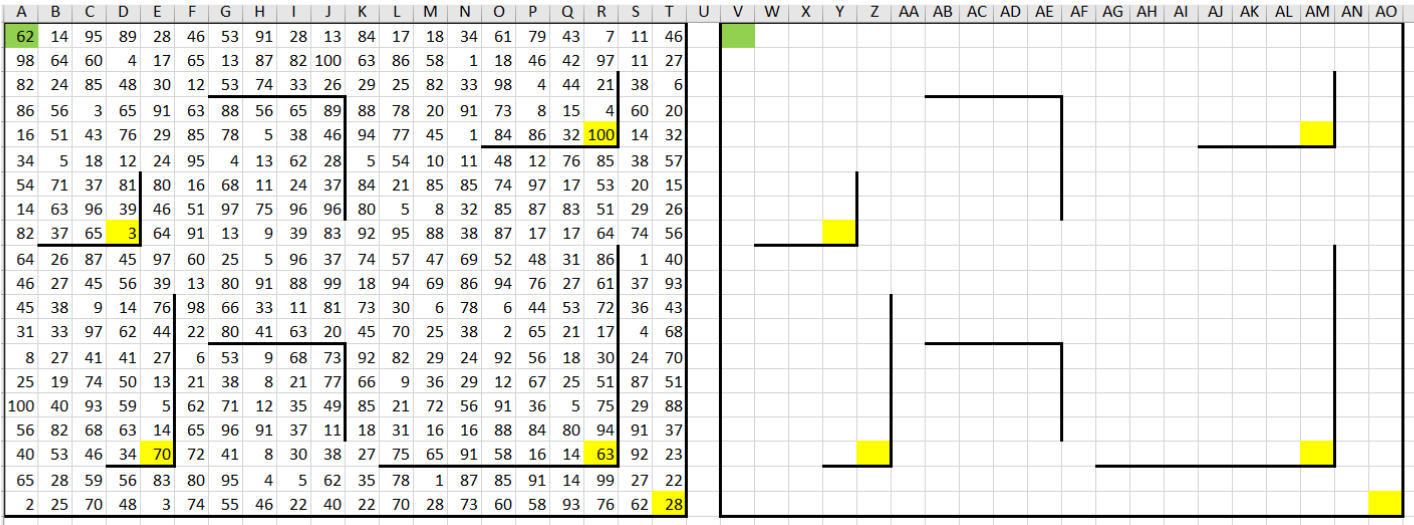
4. Заполняем начальную клетку, первую строку и первый столбец.
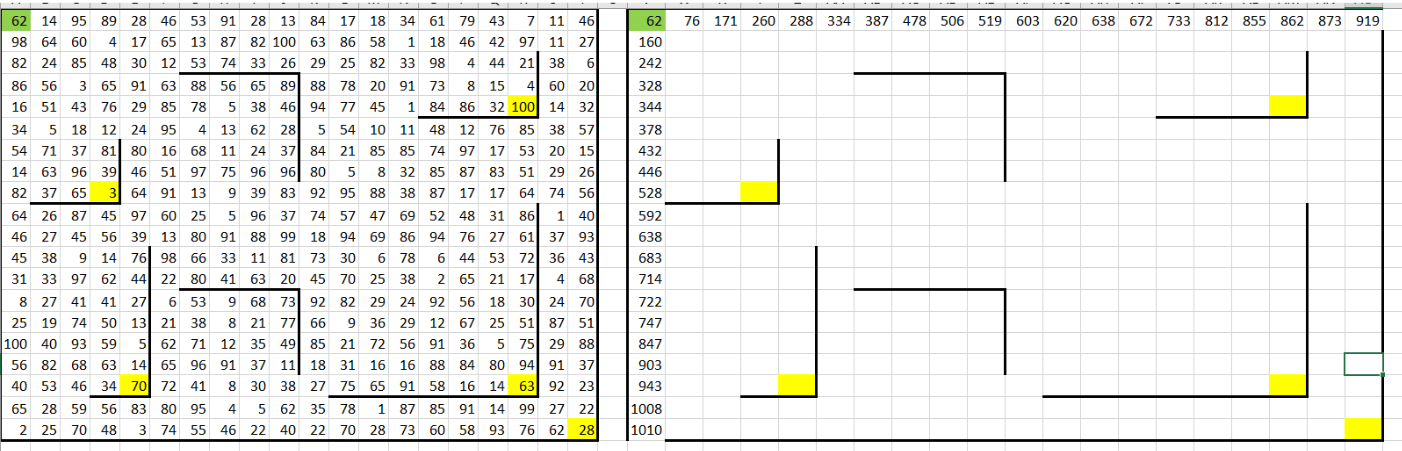
Мы начинаем с заполнения начальной клетки вспомогательной таблицы (ячейка V1). В неё вставляем формулу, которая копирует значение монет из соответствующей ячейки исходной таблицы: =A1. Это значение станет первой суммой монет, которые Робот собрал, начиная движение с этой точки.
Так как Робот может попадать в ячейки первой строки только при движении вправо, а в ячейки первого столбца – только при движении вниз, сумма монет в этих ячейках будет определяться добавлением значения текущей клетки к сумме монет из предыдущей клетки.
В итоге вспомогательная таблица начнёт заполняться значениями, которые показывают суммы монет, собранных Роботом в первой строке и первом столбце.
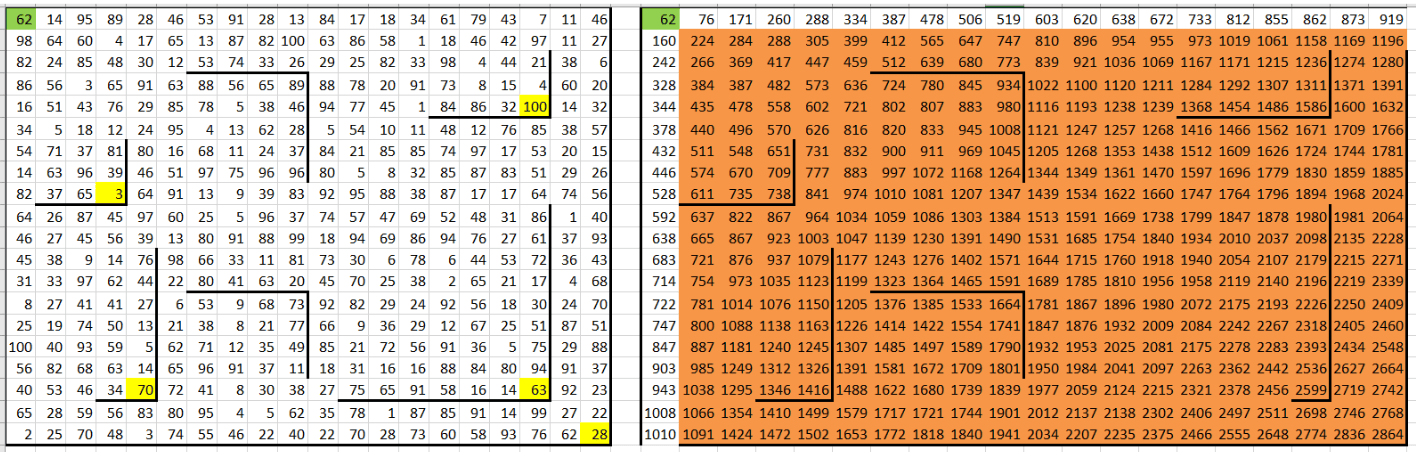
5. Заполняем остальные ячейки для поиска максимальной суммы.
Теперь наша задача — определить максимальную сумму монет, которые Робот может собрать, достигнув конечных ячеек. Для этого мы будем учитывать, что Робот может попасть в каждую клетку либо слева, либо сверху, и выберем максимальное значение из этих двух вариантов.
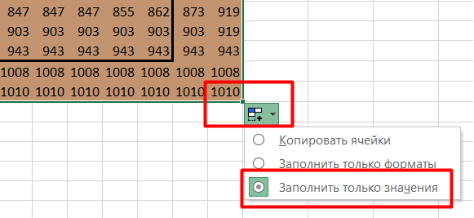
После этого протягиваем формулу по всему остальному полю вспомогательной таблицы. Таким образом, мы заполняем все ячейки значениями, соответствующими максимальной сумме монет, которые Робот может собрать, двигаясь к каждой клетке. Формулу нужно протянуть на весь диапазон, выделенный для расчетов (показан оранжевым цветом). После того, как вы растянули формулу, нажмите на «Параметры автозаполнения» и выберите «Заполнить только значения», чтобы стенки таблички сохранились:
6. Корректируем формулы для ячеек возле стен.
Если клетки расположены рядом со стенами, Робот может попасть в них только с одной стороны. Поэтому формулы для таких ячеек нужно изменить, чтобы учесть ограничение:
Корректировка формул:
1) Для ячеек справа от стен:
2) Для ячеек снизу от стен:
Для удобства можно выделить клетки возле стен другим цветом, чтобы их было проще найти и изменить формулы.
7. Теперь определяем максимальную сумму среди всех конечных клеток, выделенных жёлтым цветом. Например, в данной задаче максимальная сумма составляет 2671 монета и находится она в ячейке AO20.
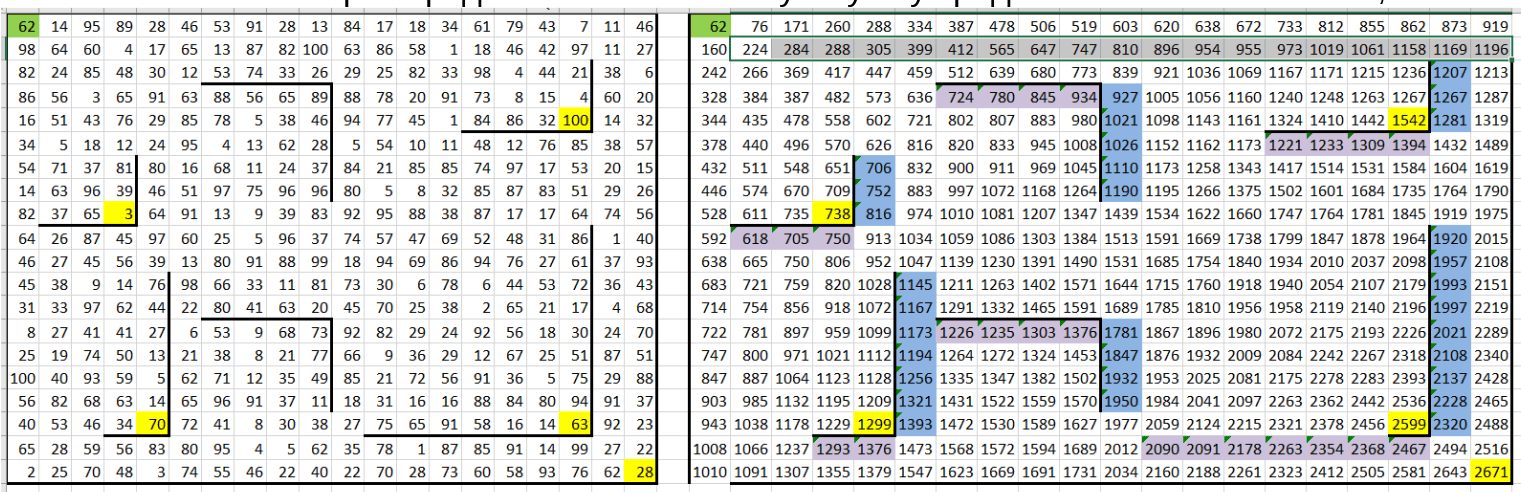
8. Поиск минимальной суммы монет:
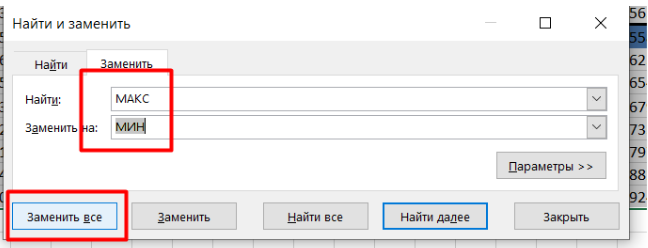
Для поиска минимальной суммы заменим во всех формулах функцию МАКС на МИН, воспользовавшись инструментом «Найти и заменить».
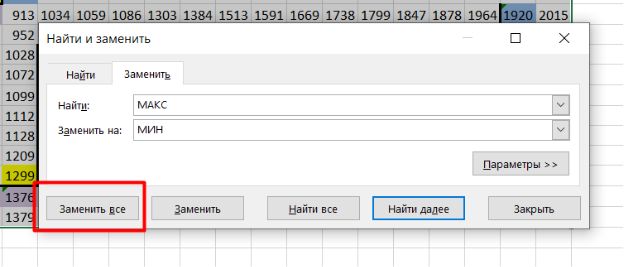
Затем найдём минимальную сумму среди конечных клеток. В данной задаче минимальная сумма составляет 419 монет и находится она в ячейке Y9.
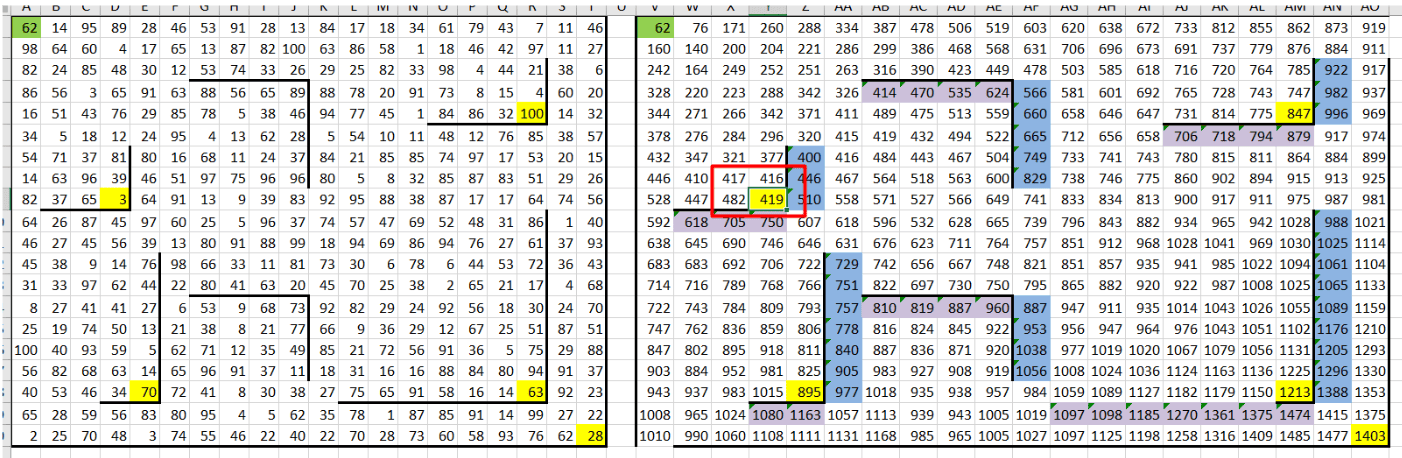
В ответе укажите два числа: сначала максимальную сумму, затем минимальную, тогда в данном случае это будет: 2671 и 419
Ответ: 2671 419
Дальше разберём задание из варианта досрочной волны (I) 2023-го года:
Квадрат разлинован на N x N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N x N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
1. Открываем файл из нашего задания, анализируем условие: нам нужно найти максимальную и минимальную сумму, который может собрать робот, пройдя из левой верхней клетки в правую нижнюю.
2. Создаем дополнительную таблицу: копируем наше поле и вставляем его в соседний диапазон справа. Это будет таблица, в которой мы будем выполнять расчеты, для наглядности выделим клетку начала движения жёлтым, а конечную клетку зелёным:
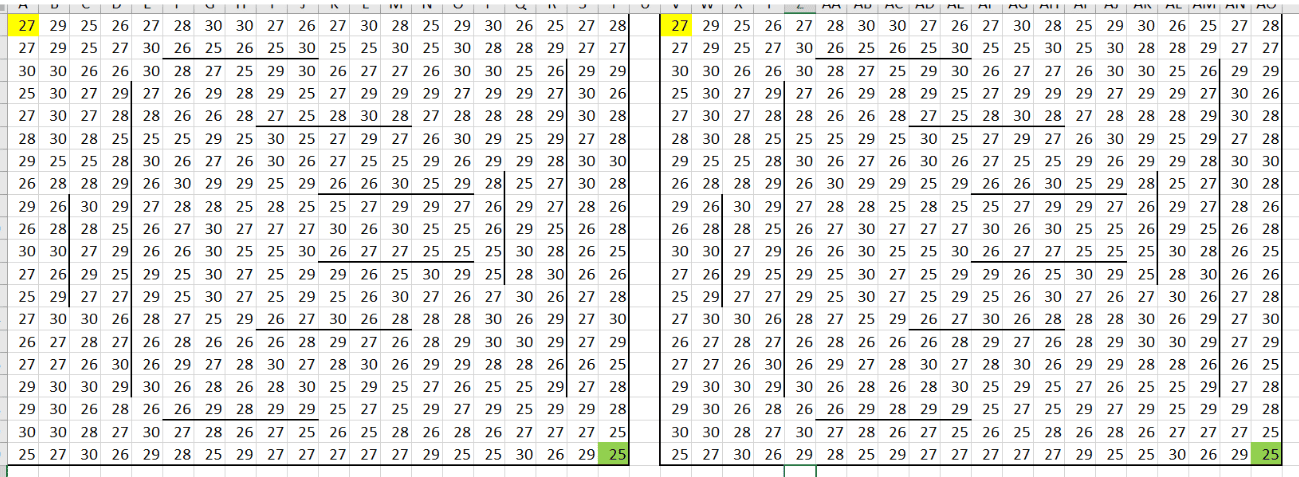
3. Очищаем правую вспомогательную таблицу от значений, копируем в левую верхнюю ячейку значение A1, и для первой строки мы заполняем каждую ячейку суммой монет из предыдущей (левой) ячейки и текущей. Вводим формулу =V1 + B1 в ячейку W1 и протягиваем её вправо до конца строки. Для первого столбца: каждая ячейка заполняется суммой монет из предыдущей (верхней) ячейки и текущей. Вводим формулу =V1 + A2 в ячейку V2 и протягиваем её вниз до конца столбца
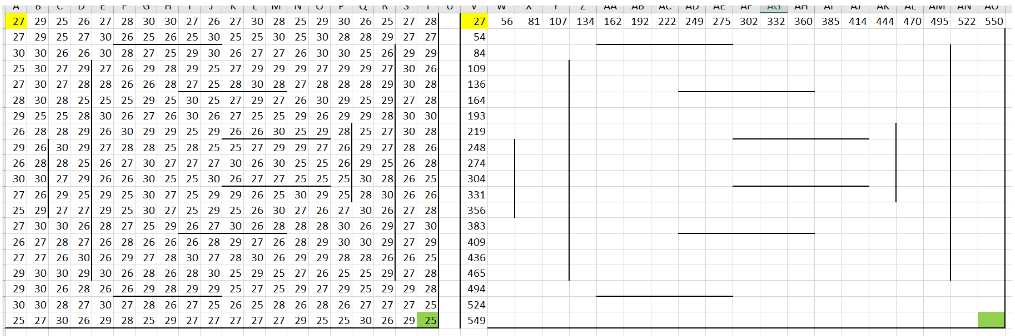
4. Для каждой ячейки мы определяем максимальную сумму, прибавляя значение текущей ячейки из исходной таблицы к наибольшей из двух возможных сумм: из клетки слева или сверху.
В ячейку W2 вспомогательной таблицы вводим формулу: =МАКС(W1; V2) + B2. Эта формула берёт максимальное значение из ячеек W1 (сверху) и V2 (слева), затем добавляет значение текущей клетки из исходной таблицы. Растягиваем эту формулу на всю таблицу (не забываем про «Параметры автозаполнения»):
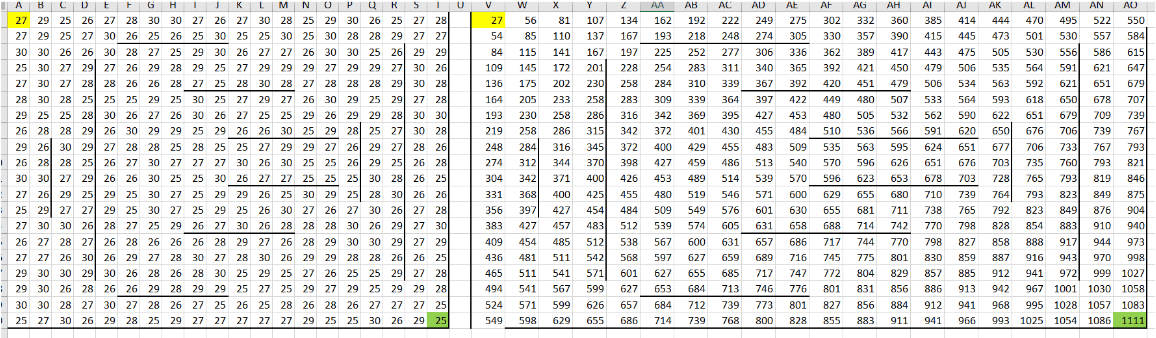
5. Корректируем формулы для ячеек справа и снизу от стен (в них мы можем попасть только сверху и слева соответственно). Для удобства можно выделить клетки возле стен другим цветом, чтобы их было проще найти и изменить формулы:
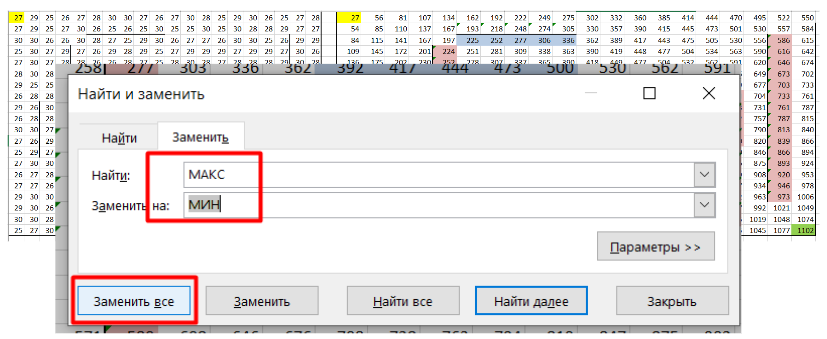
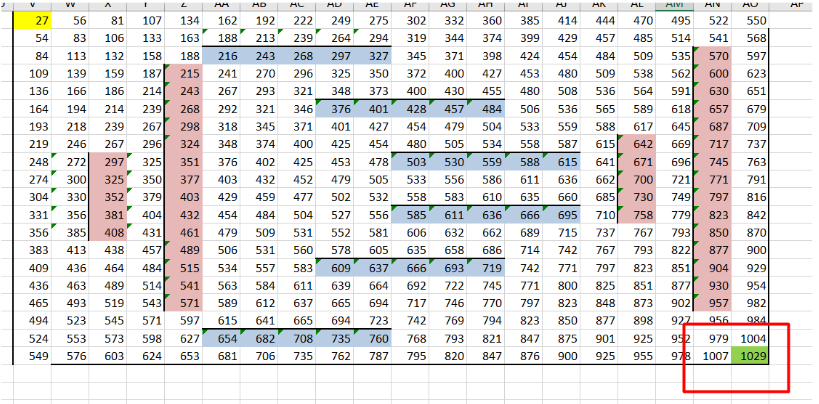
6. Запоминаем ответ, можно записать его в отдельную ячейку, теперь ищем минимальное значение: используем инструмент «Найти и заменить».
7. Нас просят указать сначала максимальную сумму, затем минимальную, тогда пишем 1102 и 1029
Ответ: 1102 1029
Следующий прототип посмотрим из основной волны 08.06.2024:
Квадрат разлинован на N x N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. В «угловых» клетках поля — тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля.
При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута.
В ответе укажите два числа: сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N x N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
1. Открываем файл задания и изучаем его условия. Задача заключается в том, чтобы найти максимальную и минимальную сумму монет, которые Робот может собрать, двигаясь из левой верхней клетки до конечной клетки (которая справа и снизу ограничена стенами).
2. Создаем вспомогательную таблицу: копируем исходное поле и вставляем его в соседний диапазон справа. Эта таблица будет использоваться для выполнения расчетов. Очищаем её содержимое и переносим значение из верхней левой клетки (A1). Для удобства выделяем начальную клетку жёлтым цветом, а конечные клетки – зелёным:
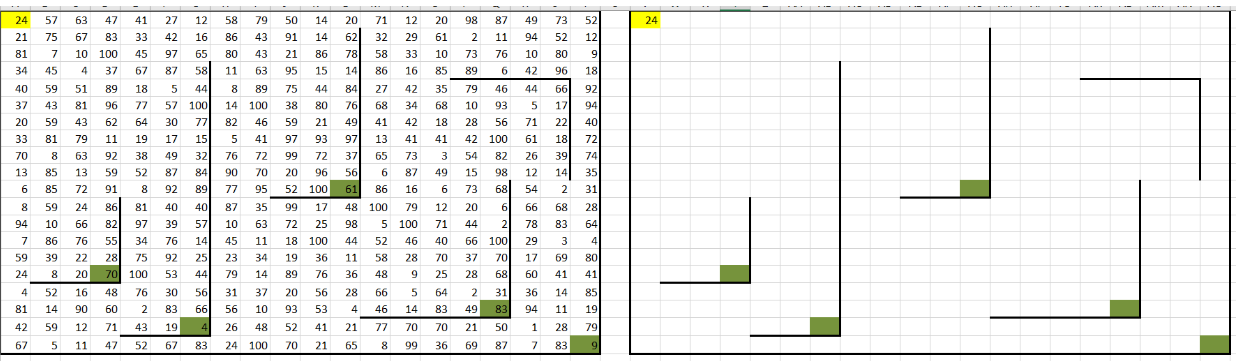
3. Для первой строки заполняем каждую ячейку, складывая монеты из предыдущей (слева) ячейки и текущей. Вводим формулу =V1 + B1 в ячейку W1 и протягиваем её вправо до конца строки.
Для первого столбца: каждая ячейка заполняется суммой монет из предыдущей (сверху) ячейки и текущей. Вводим формулу =V1 + A2 в ячейку V2 и протягиваем её вниз до конца столбца.
4. Для каждой ячейки вычисляем максимальную сумму, добавляя значение текущей ячейки из исходной таблицы к максимальному из двух вариантов: из клетки слева или сверху.
В ячейку W2 вспомогательной таблицы вводим формулу: =МАКС(W1; V2) + B2. Эта формула сравнивает значения в ячейках W1 (сверху) и V2 (слева), выбирает максимальное и добавляет значение текущей ячейки из исходной таблицы. Протягиваем эту формулу на весь диапазон таблицы, не забываем про «Параметры автозаполнения».
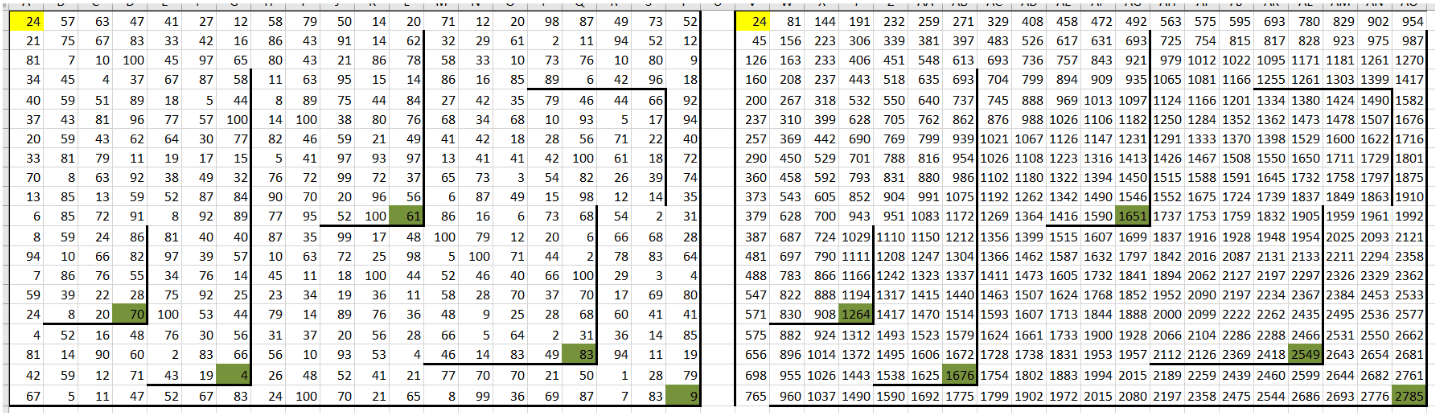
5. Корректируем формулы для ячеек, расположенных справа и снизу от стен (куда Робот может попасть только сверху или только слева соответственно). Для удобства выделяем клетки возле стен другим цветом, чтобы их было легче найти и настроить формулы.
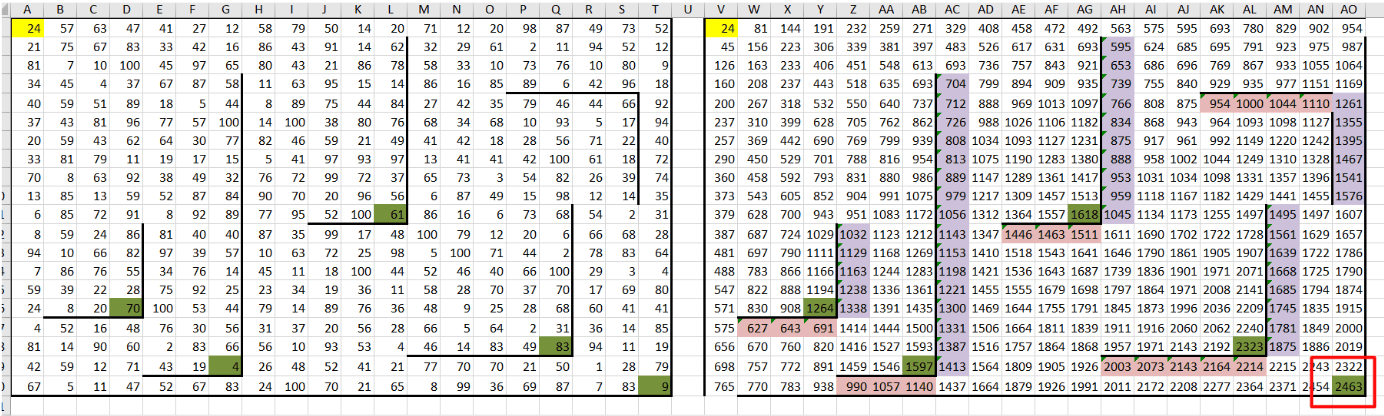
6. Видно, что наибольшим является значение в клетке AO20 (2463)
7. Запоминаем ответ, можно записать его в отдельную ячейку, теперь ищем минимальное значение: используем инструмент «Найти и заменить»:
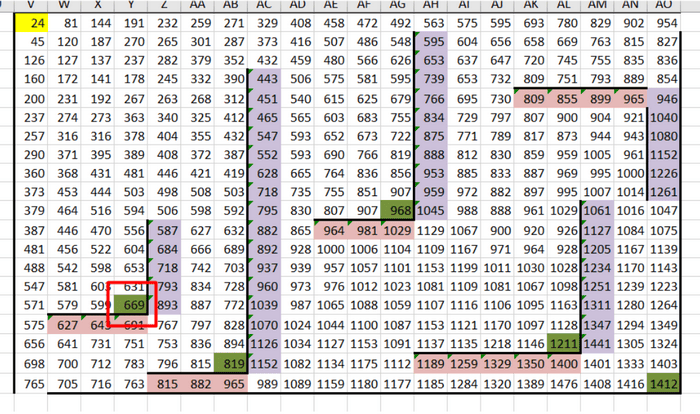
8. Минимальный является значение в ячейке Y16 (669); в ответ нас просят записать сначала максимальную сумму, затем минимальную
Ответ: 2463 669
Разберём задачу №12 ЕГЭ 2024 из варианта основной волны 04.07:
Квадрат разлинован на N x N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. В «угловых» клетках поля — тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля.
При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута.
В ответе укажите два числа: сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N x N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
1. Анализируем задание:
Открываем файл с исходными данными и внимательно читаем условие. Нам необходимо найти максимальную и минимальную сумму монет, которые Робот может собрать, перемещаясь из верхнего левого угла квадрата до одной из конечных клеток, находящихся справа и снизу (ограниченных стенами).
2. Создаем вспомогательную таблицу:Копируем поле с исходными данными и вставляем его в соседний свободный диапазон справа. Очищаем значения этой таблицы и переносим в неё значение из верхней левой клетки (A1). Чтобы не запутаться, выделяем начальную клетку жёлтым цветом, а конечные клетки — зелёным:
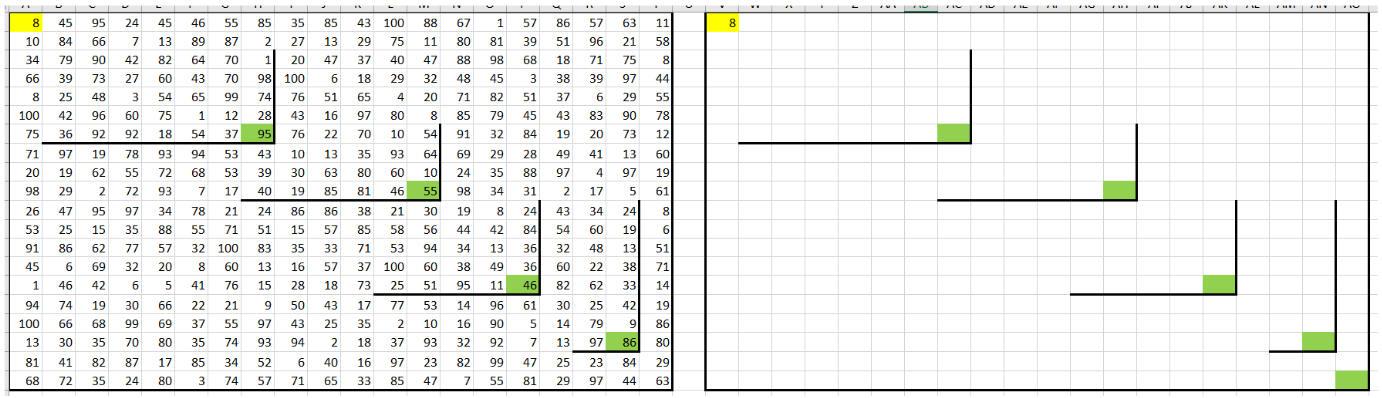
3. Заполняем первую строку и первый столбец:
4. Вычисляем максимальные суммы для всех клеток:Для остальных ячеек используем формулу, которая учитывает наибольшую сумму из двух возможных путей: из клетки сверху или из клетки слева. В ячейку W2 вставляем формулу: =МАКС(W1; V2) + B2. Эта формула добавляет значение текущей клетки к максимальной сумме из соседних. Протягиваем формулу по всей вспомогательной таблице (помним про кнопку «Заполнить только значения»):
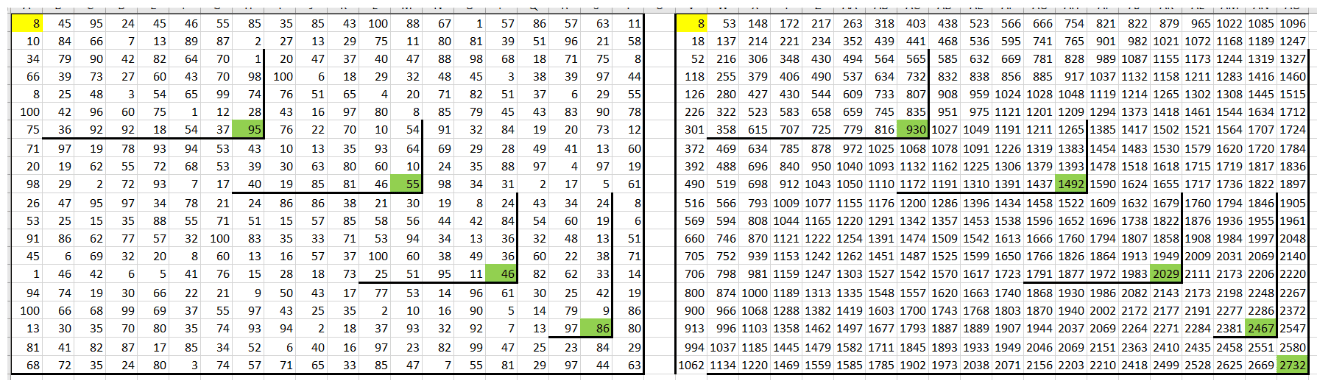
5. Корректируем формулы для ячеек возле стен:
Если клетка находится рядом со стеной, в неё можно попасть только с одной стороны:
6. Находим максимальную сумму:Смотрим конечные клетки вспомогательной таблицы. Наибольшая сумма монет будет находиться в одной из этих клеток: в нашем случае в правой нижней. Записываем это значение (2411).
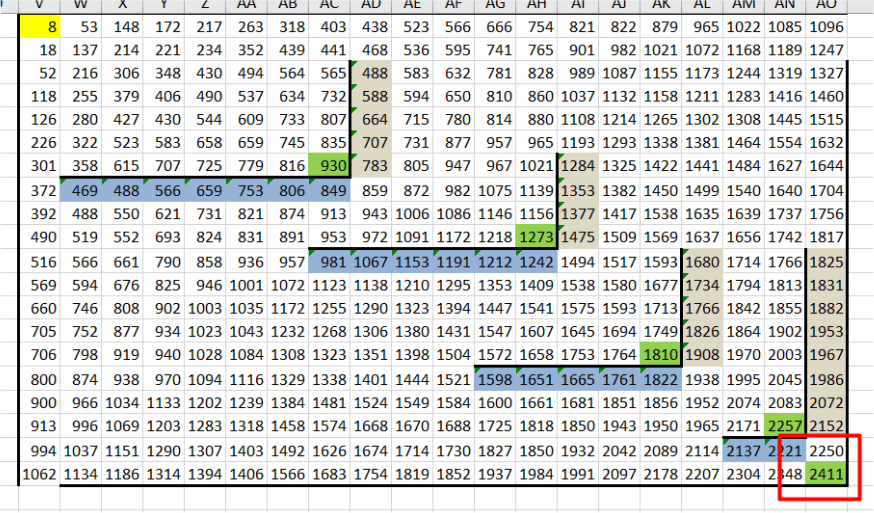
7. Ищем минимальную сумму:Теперь определяем минимальную сумму, которую может собрать Робот. Для этого можно воспользоваться инструментом «Найти и заменить».
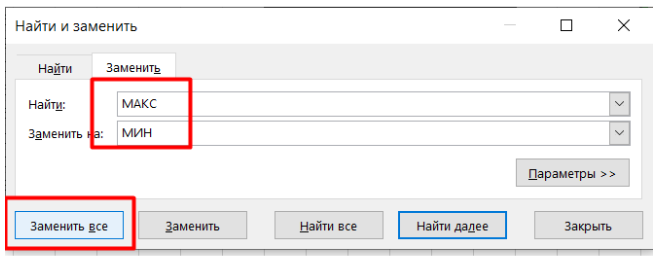
Минимальным значением будет 457
8. Записываем ответ:
Сначала указываем максимальную сумму, затем минимальную.
Ответ: 2411 457
Основная волна 2023 (III):
Квадрат разлинован на N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
В «угловых» клетках поля — тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля.
При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута.
В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
1. Изучаем задание:Открываем файл с данными и читаем условия. Задача состоит в том, чтобы найти максимальную и минимальную сумму монет, которые Робот сможет собрать, начиная движение из верхней левой клетки и заканчивая в одной из конечных клеток (справа или снизу, ограниченных стенами). Для удобства выделяем начальную клетку жёлтым цветом, а конечные — зелёным.
2. Создаем вспомогательную таблицу:Копируем исходное поле с данными и вставляем его в соседний диапазон справа. Эта таблица понадобится для выполнения расчетов. Очищаем все значения внутри неё, так как они будут заполнены формулами. Начальную клетку отмечаем, чтобы наглядно видеть начало маршрута.
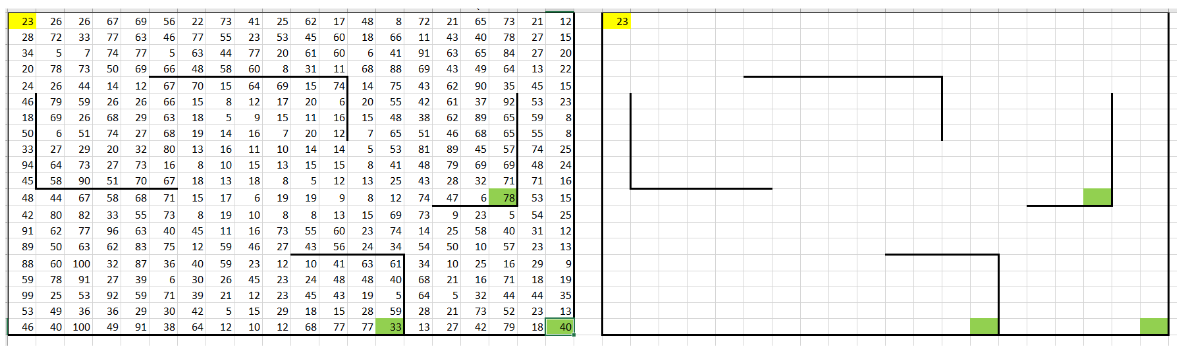
3. Заполняем первую строку и первый столбец:В начальную клетку вспомогательной таблицы вставляем формулу, копирующую значение из соответствующей ячейки исходной таблицы (A1). Для заполнения остальных ячеек:
4. Заполняем остальные ячейки для максимальной суммы:Для всех остальных ячеек таблицы заполняем значение, выбирая максимальную сумму из двух возможных путей: сверху или слева. Формула в ячейке W2: =МАКС(W1; V2) + B2. Протягиваем формулу на весь диапазон таблицы, чтобы каждая ячейка отображала максимальную сумму монет, собранных Роботом, если он попал в эту клетку.
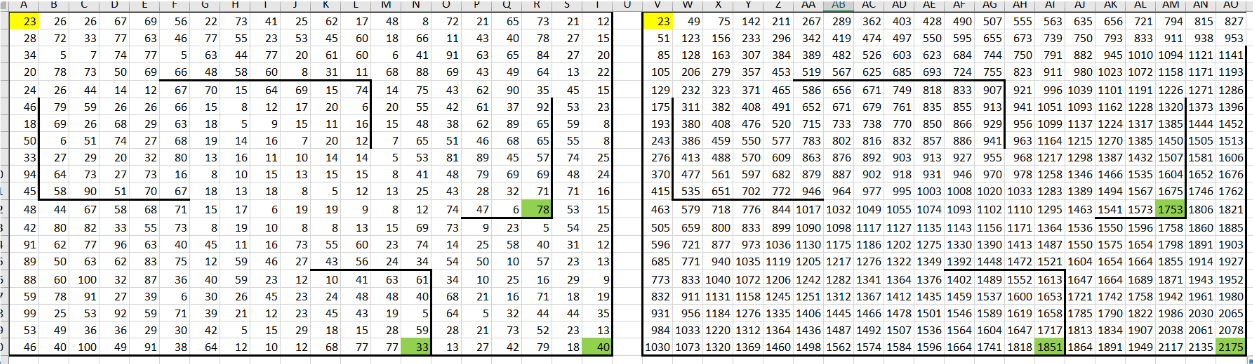
5. Корректируем формулы для клеток возле стен:Рядом со стенами Робот может попадать в ячейки только с одной стороны, поэтому корректируем формулы:
Для удобства выделяем клетки возле стен другим цветом и исправляем формулы вручную.
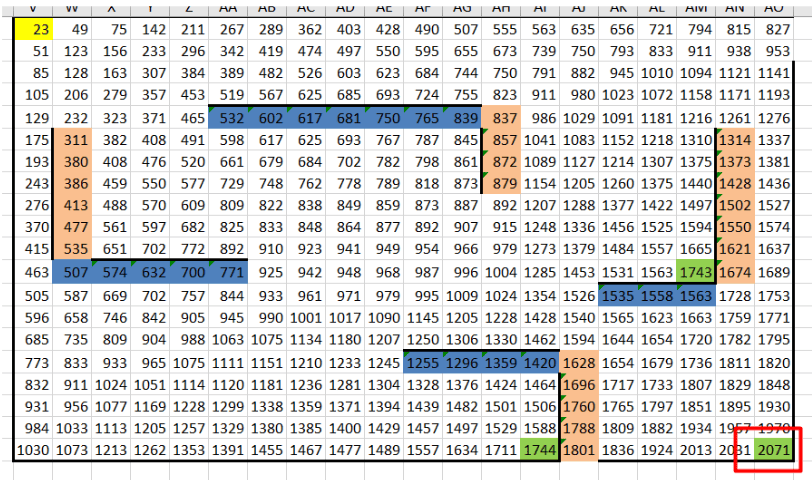
6. Находим максимальную сумму:
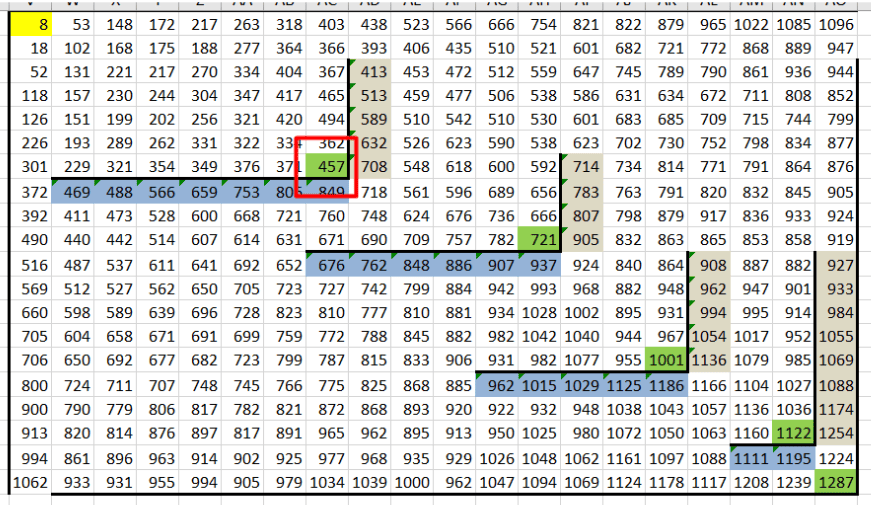
Смотрим значения в конечных клетках (зелёных). Максимальная сумма монет будет самой большой среди этих ячеек. Максимальная сумма будет 2071 монета, она расположена в клетке AO20.
7. Ищем минимальную сумму:Для нахождения минимальной суммы заменяем в формулах функцию МАКС на МИН с помощью инструмента «Найти и заменить». Затем пересчитываем таблицу и определяем минимальную сумму в конечных клетках. Минимальная сумма составляет 649 монет и находиться в клетке AM12.
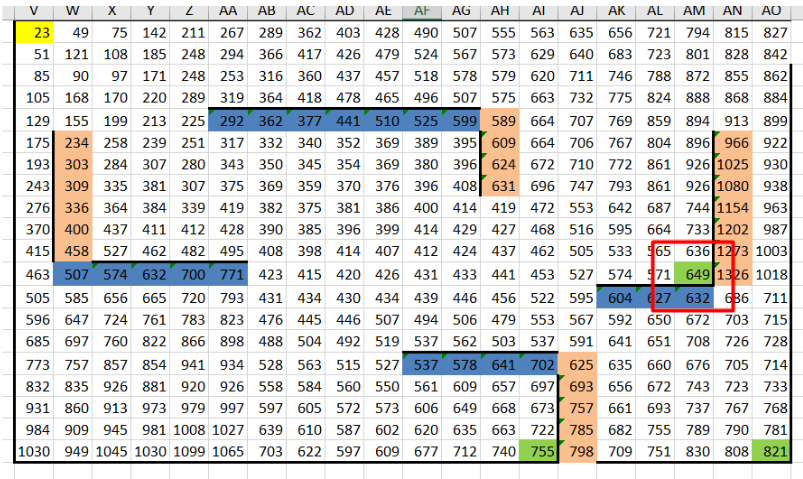
8. Записываем ответ:В ответе указываем сначала максимальную сумму, затем минимальную. В данном случае: 2071 и 649.
Ответ: 2071 649
Давайте посмотрим задачи с незначительным усложнением условия:
Квадрат разлинован на N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из трёх команд: вправо, вверх или вправо-вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю клетку, а по команде вправо-вверх — в соседнюю клетку по диагонали вправо-вверх.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Движение по диагонали допустимо, если попасть в целевую клетку возможно последовательным выполнением команд вправо и вверх либо вверх и вправо.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 10 до 120. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
В «угловых» клетках поля — тех, которые справа и сверху ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую верхнюю клетку поля.
При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой нижней клетки в конечную клетку маршрута.
В ответе укажите два числа: сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
1. Анализируем задание:Открываем файл с данными и изучаем условие. Нам нужно определить максимальную и минимальную сумму монет, которые Робот может собрать, начиная движение из левой нижней клетки и заканчивая в одной из конечных клеток (которые справа и сверху ограничены стенами). Для удобства выделяем начальную клетку жёлтым цветом, а конечные клетки — зелёным.
2. Создаем вспомогательную таблицу.Копируем исходное поле с данными и вставляем его в соседний диапазон справа. Эта таблица будет использоваться для выполнения расчетов. Удаляем все значения в этой таблице, так как её ячейки будут заполняться формулами. Обозначаем начальную клетку, чтобы ясно видеть стартовую точку.
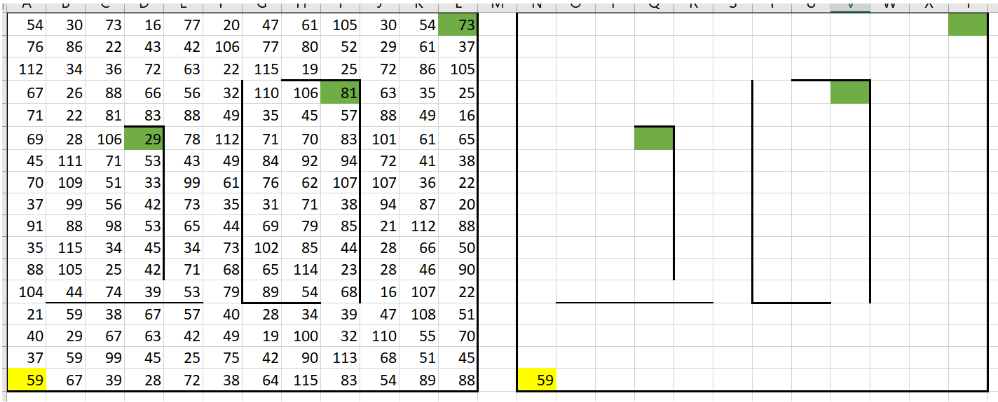
3. Заполняем первую строку и первый столбец.
В первую клетку вспомогательной таблицы вставляем формулу, которая копирует значение из соответствующей клетки исходной таблицы (A17). Для заполнения остальных ячеек:
4. Заполняем оставшиеся ячейки для нахождения максимальной суммы.Для всех других ячеек таблицы вычисляем значение, выбирая максимальную сумму из трёх возможных вариантов: снизу, слева или снизу слева (по диагонали). В ячейку O16 вводим формулу: =МАКС(N16; O17; N17) + B16. Затем протягиваем формулу на весь диапазон таблицы, чтобы каждая ячейка отображала максимальную сумму монет, которые Робот может собрать, попав в эту клетку.
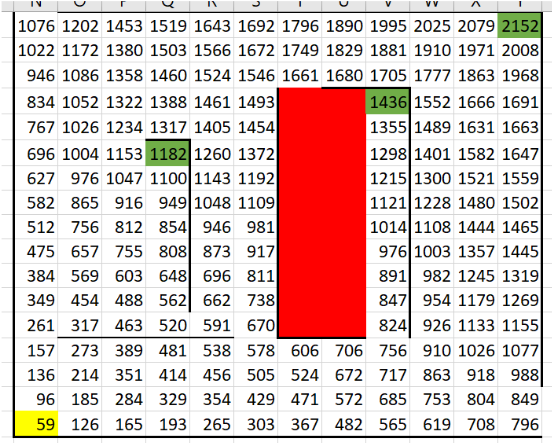
5. Заметим, что в зону, выделенной красным, мы попасть вообще не сможем, удалим оттуда значения:
6. Исправляем формулы для клеток возле стен.
Рядом со стенами Робот может попадать в некоторые клетки не со всех сторон. Поэтому:
7. Определяем максимальную сумму.
Смотрим значения в конечных клетках (зелёных). Максимальное значение из этих клеток будет наибольшей суммой монет, которые может собрать Робот.
Здесь максимальная сумма — 2152 монеты, находится в клетке Y1.
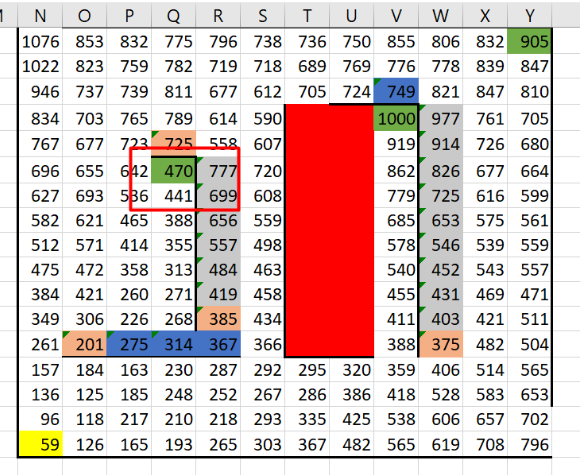
8. Определяем минимальную сумму.Для нахождения минимальной суммы используем инструмент «Найти и заменить», чтобы заменить функцию МАКС на МИН во всех формулах. Пересчитываем таблицу и смотрим минимальные значения в конечных клетках. Здесь минимальной суммой будет 470 (клетка Q6)
9. Записываем результат.В ответе сначала указываем максимальную сумму, затем минимальную.
Ответ: 2152 470
Разберём задачу №12 с ещё одним небольшим усложнением:
Квадрат разлинован N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: влево или вверх. По команде влево Робот перемещается в соседнюю левую клетку, по команде вверх — в соседнюю верхнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
В «угловых» клетках поля — тех, которые слева и сверху ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая левую верхнюю клетку поля.
При разных запусках итоговые накопленные суммы могут различаться. Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из правой нижней клетки в конечную клетку маршрута.
В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
1. Анализируем задание.Открываем файл с данными и изучаем условия. Нам нужно найти максимальную и минимальную сумму монет, которые Робот может собрать, начиная движение из правой нижней клетки и заканчивая в одной из конечных клеток (сверху и слева стена). Для удобства выделяем начальную клетку жёлтым цветом, а конечные клетки — зелёным.
2. Создаем вспомогательную таблицу.Копируем исходное поле с данными и вставляем его в соседний диапазон справа. Это будет таблица, где мы будем выполнять расчёты. Очищаем все значения в таблице, так как ячейки будут заполнены формулами.
3. Заполняем последнюю строку и последний столбец.В правую нижнюю клетку вспомогательной таблицы вставляем формулу, копирующую значение из соответствующей клетки исходной таблицы. Для остальных ячеек:
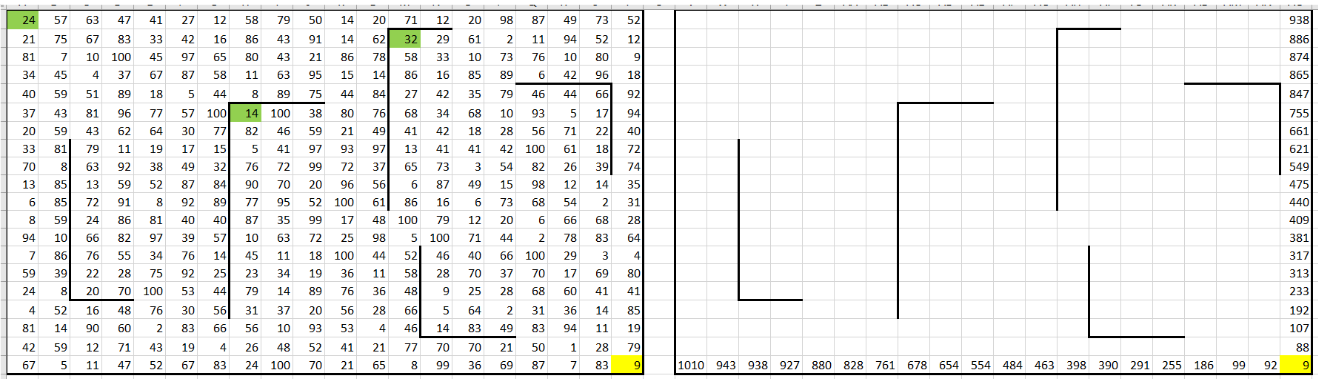
4. Заполняем остальные ячейки для нахождения максимальной суммы.Для всех остальных ячеек таблицы заполняем значения, выбирая максимальную сумму из двух возможных путей: из клетки справа или из клетки ниже. Например, в ячейке AN19 вводим формулу: =МАКС(AN20; AO19) + S19. Затем протягиваем формулу на весь диапазон таблицы, чтобы каждая ячейка отображала максимальную сумму монет, собранных Роботом при попадании в эту клетку.
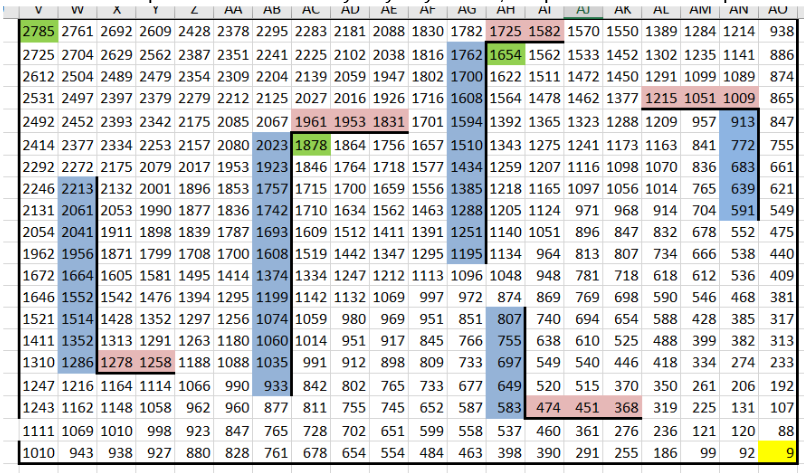
5. Корректируем формулы для клеток возле стен.Клетки, расположенные рядом со стенами, требуют корректировки формул, так как Робот может попасть в них только с одной стороны:
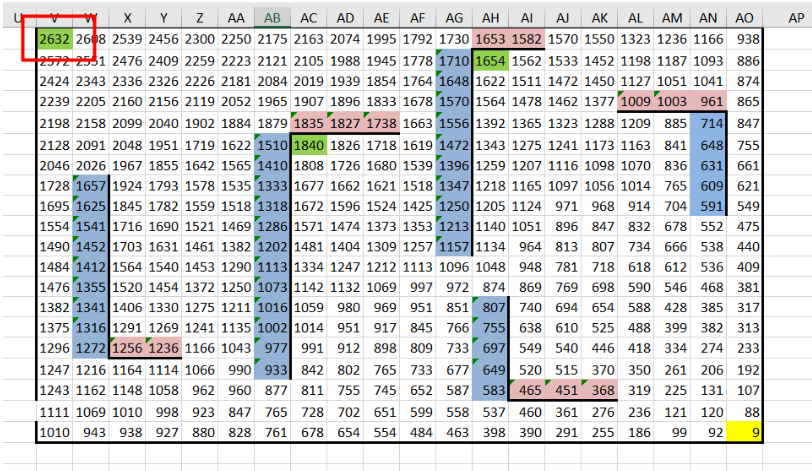
6. Находим максимальную сумму.Смотрим значения в конечных клетках (зелёных). Самое большое значение среди них будет максимальной суммой монет, которые может собрать Робот.
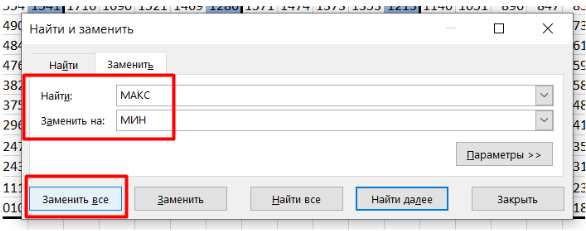
7. Ищем минимальную сумму.Чтобы найти минимальную сумму, заменяем функцию МАКС на МИН во всех формулах с помощью инструмента «Найти и заменить». Пересчитываем таблицу и определяем минимальное значение среди конечных клеток.
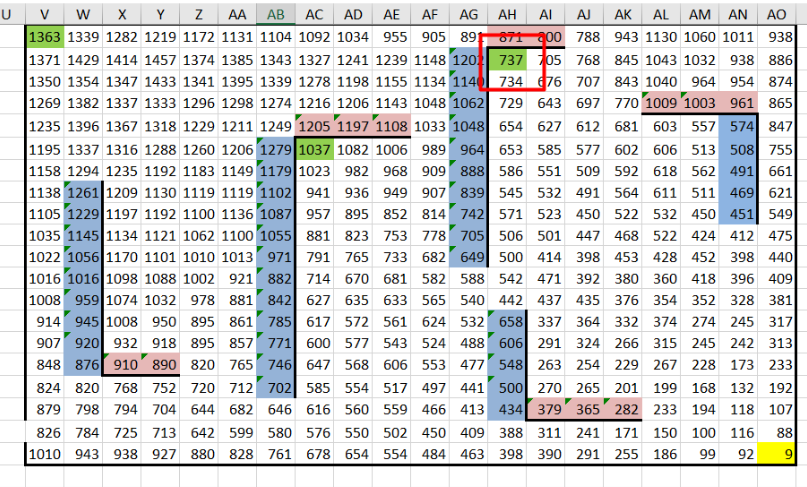
8. Записываем результат.В ответе указываем сначала максимальную сумму, затем минимальную. Для данной задачи это: 2632 и 737
Ответ: 2632 737
Ну и заключительное упражнения для закрепления материала:
Квадрат разлинован на N×N клеток (1 <N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: влево или вниз. По команде влево Робот перемещается в соседнюю левую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. В «угловых» клетках поля (тех, которые слева и снизу ограничены стенами) Робот продолжать движение не может, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая левую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться.
Определите максимальную и минимальную денежные суммы среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из правой верхней клетки в конечную клетку маршрута. В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение:
1. Единственное отличие от классической задачи данного типа заключается в том, что Робот начинает из правого верхнего угла и движется влево и вниз. Выполняем уже знакомый нам алгоритм: копируем таблицу, удаляем числовые значения, начальную и итоговые клетки отмечаем жёлтым и зелёными цветами, переносим начальную клетку из исходной таблицы, столбец и строку получаем обычной суммой предыдущих значений и значений, соответствующих данной клетке, но в исходной таблице:
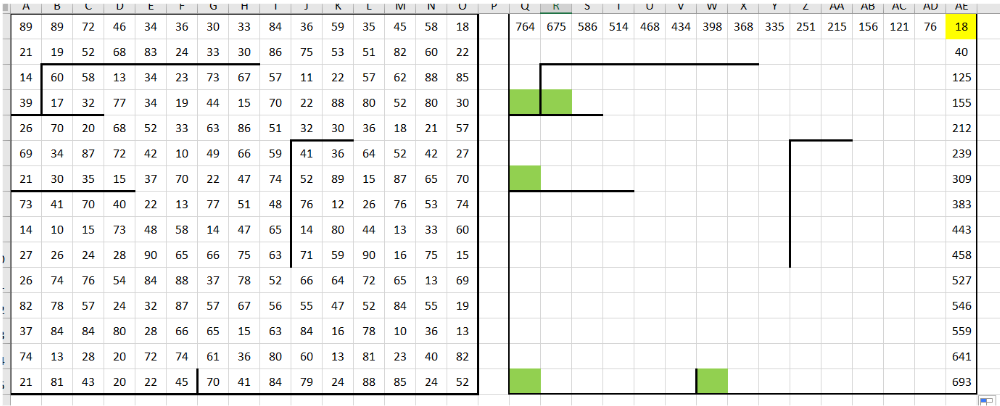
2. Остальные значения получаем как максимальное от клетки слева и сверху плюс соответствующее значение из исходной таблицы, но не забываем про случаи, когда в клетку мы можем попасть только справа или только сверху:
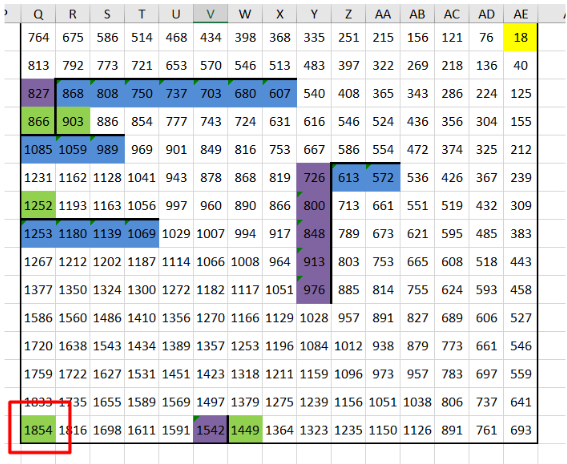
3. Легко заметить максимальное значение: 1854
4. Чтобы найти минимальную сумму, заменяем функцию МАКС на МИН во всех формулах с помощью инструмента «Найти и заменить». Пересчитываем таблицу и определяем минимальное значение среди конечных клеток
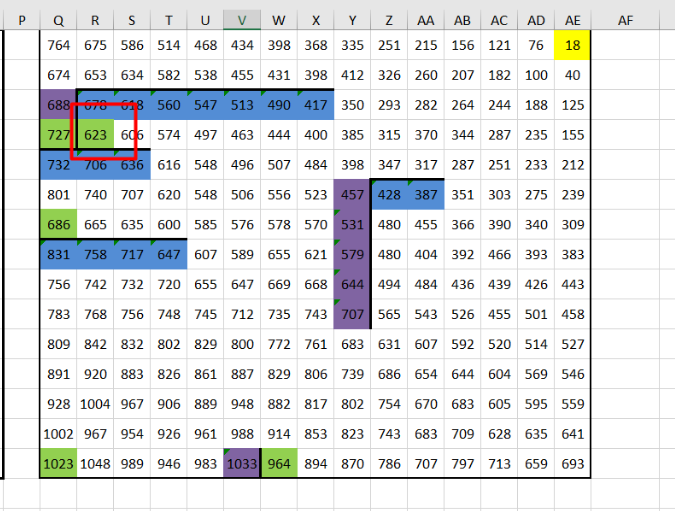
Ответ: 1854 623
Задание №18 ЕГЭ по информатике — это задание продвинутого уровня сложности, проверяющее навыки работы с электронными таблицами, алгоритмическое мышление и умение анализировать данные. Основная цель — корректно определить максимальные и минимальные суммы монет, которые может собрать робот, следуя заданным условиям движения.
Основные аспекты для успешного выполнения:
1. Четкое понимание условий задачи.
Перед началом решения важно внимательно изучить условие, чтобы понять, откуда начинается движение робота, какие команды он может выполнять, и где расположены конечные клетки. Это поможет правильно выделить стартовые и конечные точки в таблице.
2. Создание вспомогательной таблицы.Вспомогательная таблица — это ключевой инструмент для вычислений. Убедитесь, что все значения в ней правильно очищены и заполнены, а начальная и конечные клетки выделены для удобства.
3. Пошаговое заполнение таблицы.
4. Корректировка формул возле стен.Учитывайте ограничения на движение возле стен. Для таких клеток робот может попасть только с одной стороны, что требует корректировки формул. Используйте цвета для выделения этих клеток и изменения логики их заполнения.
5. Использование инструментов Excel.
Лайфхаки для решения:
1. Выделяйте клетки визуально.Начальную клетку можно выделить зелёным, а конечные — жёлтым. Это облегчит ориентирование в таблице и проверку результатов.
2. Используйте промежуточные проверки.На каждом этапе выполнения задачи проверяйте, правильно ли заполнены значения в промежуточных клетках, чтобы исключить ошибки на ранних этапах.
3. Оптимизируйте расчеты.Для больших таблиц можно использовать фильтры и функции для быстрого выделения нужных диапазонов. Это ускорит вычисления и упростит проверку результатов.
4. Обращайте внимание на уникальные условия задачи.Например, дополнительные команды движения (вверх-вправо, диагонали) или особые ограничения возле стен требуют корректировки общего алгоритма.
5. Логичность результата.Всегда проверяйте итоговые значения на соответствие условиям задачи. Например, максимальная сумма должна быть логически больше минимальной, а их расположение должно совпадать с указанными ограничениями.
Что важно запомнить:
Следуя этим рекомендациям, вы сможете успешно решать задания такого типа на экзамене.
Удачи!
В варианте ЕГЭ-2025 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
