Это задание относится к базовому уровню и направлено на проверку наших навыков в кодировании и декодировании информации. Составители экзамена хотят удостовериться, что мы понимаем основные принципы работы с информацией и умеем правильно её интерпретировать.
Давайте разберёмся с ключевыми понятиями, которые могут быть полезны для успешного решения задачи.
Кодирование и декодирование информации — это процессы преобразования данных из одного формата в другой. Кодирование переводит информацию из исходной формы в закодированное представление, а декодирование выполняет обратное действие, восстанавливая первоначальный вид данных. Эти процессы используются для передачи, хранения и обработки информации в понятном для машины формате.
Двоичный код — это метод представления данных, где используются только два символа, обычно 0 и 1. Каждый символ называется двоичным разрядом, и такая система применяется в компьютерах и цифровых устройствах.
Таблица с примерами двоичных кодов.
Для лучшего понимания двоичного кодирования можно представить простую таблицу, в которой показаны примеры кодов для разных символов.
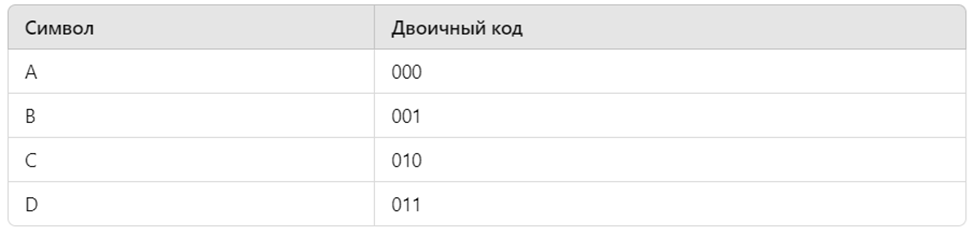
Равномерный код — это код, в котором все кодовые слова имеют одинаковую длину. В таком коде каждый символ представляется одинаковым количеством знаков. Например, для букв A, B, C и D можно задать двоичный код: A — 00, B — 01, C — 10, D — 11. Поскольку длина всех кодов одинаковая, этот код считается равномерным.
Неравномерный код — это код, в котором кодовые слова имеют разную длину. Такой код используется, если длина кодов для символов может меняться. Пример: для букв A, B, C и D коды могут быть заданы так: A — 00, B — 100, C — 101, D — 1010. В этом случае длина кодов разная, и такой код называют неравномерным.
Таблица сравнения равномерных и неравномерных кодов.
Для наглядности можно добавить таблицу, сравнивающую равномерный и неравномерный коды для тех же символов.
Однозначно декодируемый код — это код, в котором любую последовательность кодовых слов можно расшифровать одним способом. Равномерные коды всегда однозначно декодируемы, а для неравномерных кодов требуется выполнение специальных условий, чтобы гарантировать единственный способ расшифровки.
Также для решения задачи нам понадобится понимать прямое условие Фано и алгоритм построения бинарного дерева кодирования.
Прямое условие Фано — это правило, обеспечивающее однозначное декодирование для неравномерного кода. Оно гласит, что ни одно кодовое слово не должно быть началом другого. Коды, которые удовлетворяют этому условию, называются префиксными.
Пример таблицы истинности для условия Фано.
Чтобы визуально показать, что ни один код не является префиксом другого, можно использовать такую таблицу.
Здесь видно, что каждый код уникален и не пересекается с другими, что соответствует условию Фано.
Теперь разберёмся, как построить бинарное дерево кодирования, чтобы выбрать минимальные кодовые слова для оставшихся букв, не нарушая условия Фано.
Бинарное дерево кодирования — это структура данных, где каждый узел может иметь не более двух «потомков»: левого и правого. В бинарном дереве каждый путь от корня до узла формирует уникальный код для каждого символа. Это упрощает выбор кодов, которые не будут являться префиксами других кодов, что соответствует прямому условию Фано.
Алгоритм построения бинарного дерева кодирования:
Пример бинарного дерева:
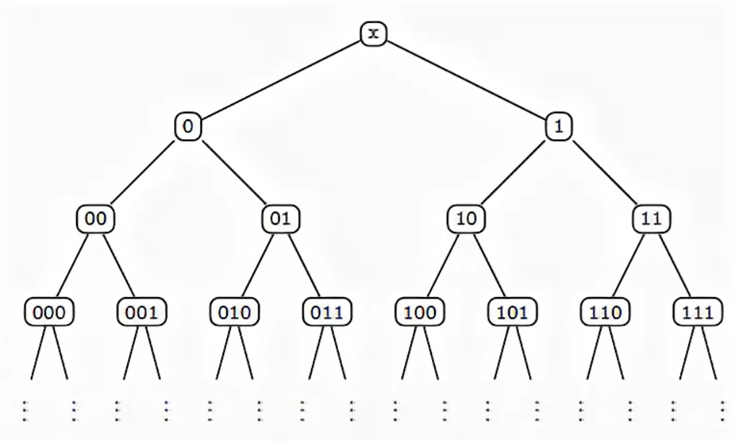
Перейдём к примеру решения прототипов задач:
Разберём задачу №4 ЕГЭ 2024 из демоверсии ФИПИ.
По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж и З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
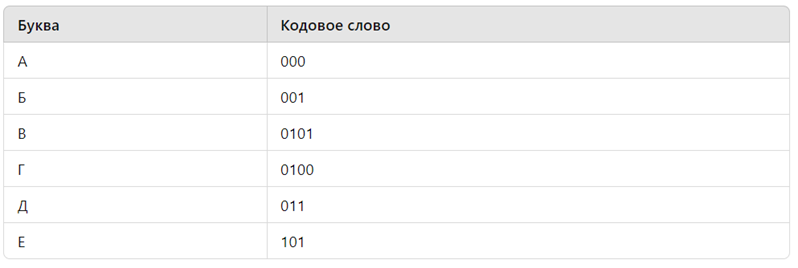
Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?
В ответе запишите суммарную длину кодовых слов для букв Ж и З.
Способ 1: аналитический
1. В задаче на экзамене будет сказано, что такое условие Фано, но на всякий случай давайте вспомним, что это: это условие гласит, что ни одно кодовое слово не должно быть началом другого. Нам нужно выбрать коды для букв Ж и З, чтобы длина была минимальной и условие Фано соблюдалось.
2. Анализируем условие нашей задачи: нам известны кодовые слова для некоторых букв. Важно обращать внимание, что от нас требуют, в условии может быть подвох, например, если нужно будет обратное условие Фано или сообщения будут содержать не 8 букв, а весь алфавит.
3. Проверяем коды минимальной длины:
Начнём с минимально возможной длины кодов и проверим, какие варианты подходят.
Значит коды длиной 1 (как «0», так и «1») не подходят, так как оба нарушают условие Фано.
4. Проверяем коды длины 2: всего существует 4 варианта кодов длины 2 («00», «01», «10», «11»)
Запоминаем это, но пока не присваиваем коду наши буквы.
5. Проверка кодов длиной 3 для оставшейся буквы: ищем подходящий код среди свободных кодов длиной 3.
Только теперь мы можем с уверенностью присвоить код «11» букве Ж, а код «100» букве З. Почему важно не торопиться присваивать нашу букву коду минимальной длины: в нашем примере всё бы удачно получилось, но могло случиться такое, что мы «заблокировали» ветку «11», а следующий свободный код был бы уже длины 5, тогда наш ответ получился бы 7, а если бы мы продолжили ветку «11», то получили бы 2 кода длины 3, что в сумме дало бы 6 и являлось бы правильным ответом. Будьте внимательны!
6. Считаем сумму длин кодовых слов. Для букв Ж и З мы выбрали следующие коды:
Суммарная длина кодов составляет 2 + 3 = 5.
Ответ: 5
Способ 2: построение бинарного дерева
1. Строим бинарное дерево, которое будет соответствовать нашему условию задачи (узлы соответствуют буквам, красным крестом обозначаем, что дальше дерево продолжать не можем, потому что не будет выполняться условие Фано):
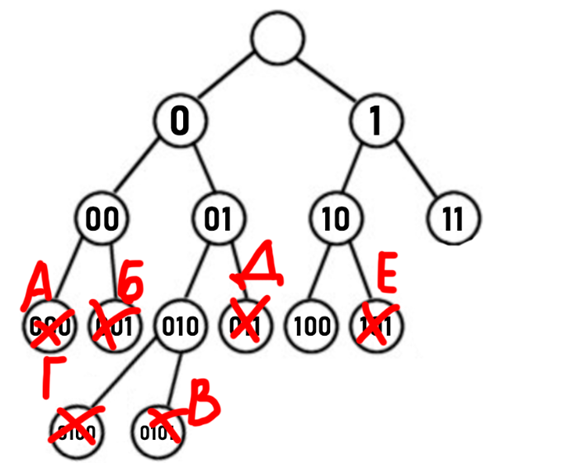
2. Сейчас мы прекрасно видим, что у нас есть пустые минимальные коды «11» и «100», которые мы можем присвоить нашим буквам Ж и З.
3. Считаем сумму длин кодовых слов. Для букв Ж и З мы выбрали следующие коды:
Суммарная длина кодов составляет 2 + 3 = 5.
Ответ: 5
Разберём задание №4 из варианта досрочной волны 2024:
По каналу связи передаются шифрованные сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж и З. Для передачи используется неравномерный двоичный код. Кодовые слова для некоторых букв известны:
Укажите кратчайшее кодовое слово для буквы З, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решим это задание, построив бинарное дерево:
1. Строим бинарное дерево, которое будет соответствовать нашему условию задачи (узлы соответствуют буквам, красным крестом обозначаем, что дальше дерево продолжать не можем, потому что не будет выполняться условие Фано):
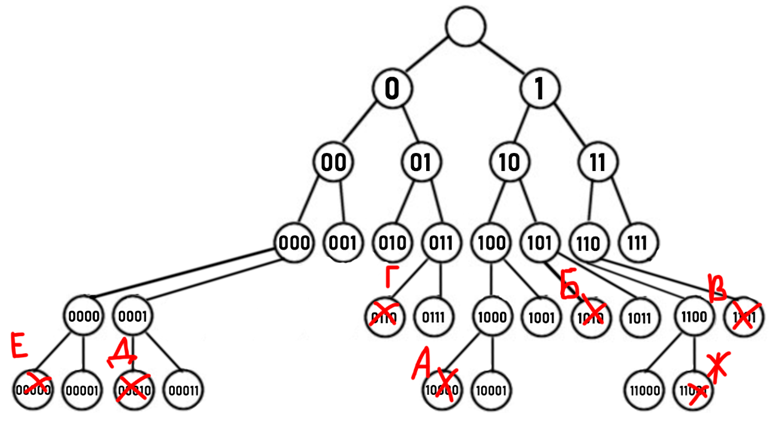
2. По нашему дереву видно, что свободных кодов минимальной длины несколько («001», «010», «111»), по условию нам нужен код с наименьшим числовым значением, значит выбираем «001».
Ответ: 001
Дальше посмотрим задачу из варианта с основной волны 07.06.24:
По каналу связи передаются сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для кодирования букв используются кодовые слова:
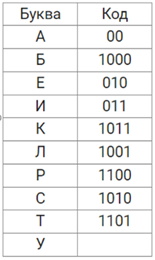
Укажите кратчайшее кодовое слово для буквы У, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решим аналитикой:
1. Проверяем коды минимальной длины:
Начнём с минимально возможной длины кодов и проверим, какие варианты подходят.
Значит коды длиной 1 (как «0», так и «1») не подходят, так как оба нарушают условие Фано.
2. Проверяем коды длины 2: всего существует 4 варианта кодов длины 2 («00», «01», «10», «11»)
Значит коды длины 2 не подходят, так как они нарушают условие Фано.
3. Проверяем коды длины 3: пойдём по возрастанию:
«000» и «001» мы использовать не можем, потому что буква А уже «заблокировала» этот путь; «010» занят буквой Е; 011 занят буквой И; «100» не подходит, т.к. с него начинается код для Б, «101» занят буквой С; со «110» начинается код для Т; а вот «111» как раз удовлетворяет условию Фано, то есть подходит нам и является наименьшим подходящим (т.к. все меньшие варианты мы перебрали)
Ответ: 111
Перейдём к основной волне 19.06.24 (вариант из Центра России):
По каналу связи передаются сообщения, содержащие только буквы: Б, К, Л, О, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 1001, К — 11.
Для трёх оставшихся букв Л, Н и О кодовые слова неизвестны. Какое наименьшее количество двоичных знаков требуется для кодирования слова КОЛОКОЛ?
Примечание: Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решим это задание, построив бинарное дерево:
1. Строим бинарное дерево, которое будет соответствовать нашему условию задачи (узлы соответствуют буквам, красным крестом обозначаем, что дальше дерево продолжать не можем, потому что не будет выполняться условие Фано):
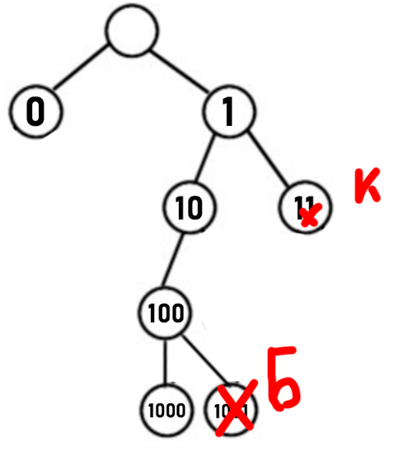
2. Нам нужно закодировать ещё 3 буквы: Л, Н и О, но для слова КОЛОКОЛ нам нужны только К, Л и О, и количество двоичных знаков для кодирования слова должно быть наименьшим, т.е. букву Н мы можем закодировать самым длинным кодом (например, «1000»), она нам не нужна для слова.
3. Обращаем внимание на количество букв Л и О в слове КОЛОКОЛ: 2 буквы Л и 3 буквы О, это нам нужно для того, чтобы понять, каким способом мы можем оптимально закодировать наши буквы, то есть букве О можем присвоить код «0», а Л присвоим «101», получим 1*3 + 3*2 = 9 двоичных знаков. Или мы можем продолжить «0»: О присвоим «00», а Л – «01», тогда получим 2*3 + 2*2 = 10 двоичных знаков – этот вариант хуже, потому что он больше, следовательно мы выбираем первый вариант.
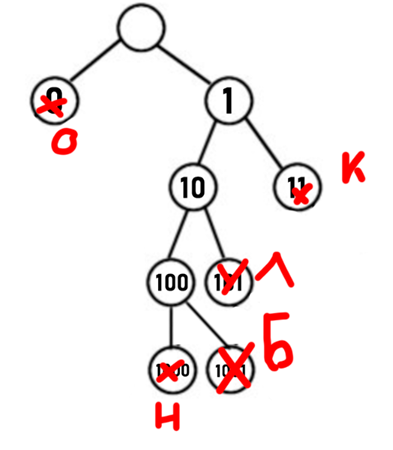
4. Вспоминаем, что по условию нам нужна сумма двоичных знаков для слова КОЛОКОЛ, считаем: 1*3 + 3*2 + 2*2 = 13 (К закодирована «11» по условию).
Ответ: 13
Теперь давайте разберём задание №4 из варианта основной волны 19.06.24 (Сибирь):
По каналу связи передаются сообщения, содержащие только буквы из набора: А, Т, К, С, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Н — 11, С — 101.
Для трёх оставшихся букв К, Т и А кодовые слова неизвестны. Какое количество двоичных знаков требуется для кодирования слова КАСАТКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Примечание: Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решим аналитикой:
1. Нам даны кодовые слова для некоторых букв:
2. У нас остаются три буквы — K, T и A. Так как в задаче требуется минимальное количество двоичных знаков, нам нужно построить кодовые слова для этих букв, минимизируя длину кода. Также нужно удовлетворить условию Фано. Считаем количество этих букв в слове КАСАТКА: А встречается 3 раза, К – 2 раза, и Т – 1. Тогда у буквы А должен быть минимальный код
3. Проверяем возможные варианты: А закодируем «0», тогда для К и Т остаются продолжения «100»: «1000» и «1001», считаем сумму: 3*1 + 2*4 + 1*4 = 15. Есть другой вариант: продолжить «0», закодировать А «00», К «01» и для Т останется «100»: 2*3 + 2*2 + 3*1 = 13 – этот вариант лучше и будет наименьшим, потому что любой другой будет длиннее.
4. Считаем сумму двоичных знаков для слова КАСАТКА: 2*3 + 2*2 + 3*1 + 3*1 = 16 (по условию буква С кодируется «101»). Пишем ответ
Ответ: 16
Перейдём к основной волне 2023го года.
Решим это задание, построив бинарное дерево.
По каналу связи передаются шифрованные сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж, З. Для передачи используется неравномерный двоичный код. Для шести букв используются кодовые слова:
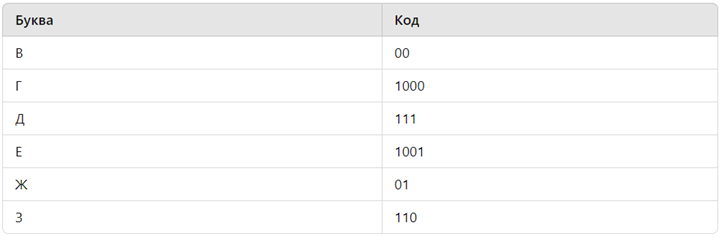
Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?
В ответе запишите суммарную длину кодовых слов для букв А и Б.
Примечание: Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение:
1. Строим бинарное дерево, которое будет соответствовать нашему условию задачи (узлы соответствуют буквам, красным крестом обозначаем, что дальше дерево продолжать не можем, потому что не будет выполняться условие Фано):
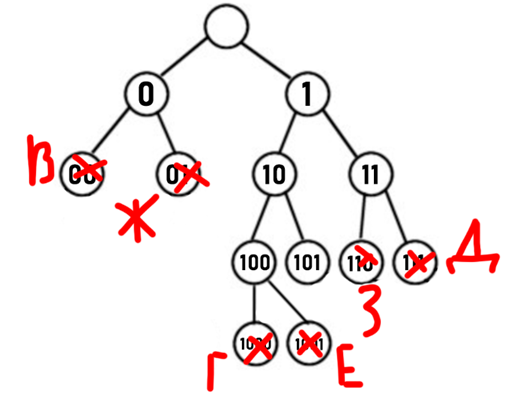
2. Мы видим, что свободный узел у нас только один («101»), а закодировать нужно 2 буквы, значит мы его продлеваем до «1010» и «1011» - этим кодам мы и присваиваем наши буквы А и Б.
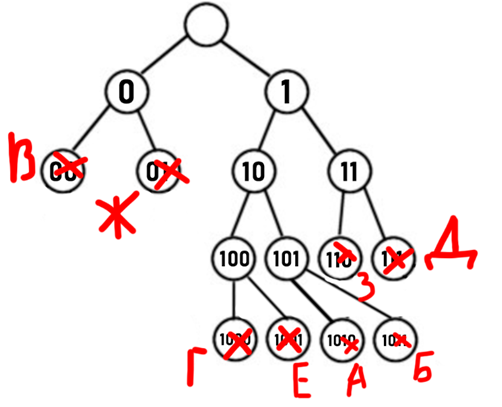
3. Считаем сумму: 4 + 4 = 8
Ответ: 8
Посмотрим досрочную волну того же года:
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, В, Г, Д, Е, Ж, З, И, К. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова:
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решим аналитикой:
1. Перебираем все возможные варианты двоичных кодов по возрастанию:
«0» начало кода буквы А, «1» - начало кода буквы Ж; «00», «01», «10» и «11» - соответственно начала кодов для букв А, Е, И и Ж, то есть тоже не подходят; перебираем коды из 3х знаков: «000» - занято В, «001» - начало А, «010» - начало Е; «011» - начало З, «100» занято К, «101» - занято И, «110» свободно, значит подходит нам и является наименьшим числовым значением, потому что все меньшие мы перебрали.
Ответ: 110
Посмотрим вариант с основной волны 2022-го года:
По каналу связи передаются сообщения, содержащие только буквы из набора: А, В, И, Н, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Р — 0, Т — 11.
Для четырёх оставшихся букв А, В, И и Н кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова ИНВАРИАНТ, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Решим это задание, построив бинарное дерево:
1. Строим бинарное дерево, которое будет соответствовать нашему условию задачи (узлы соответствуют буквам, красным крестом обозначаем, что дальше дерево продолжать не можем, потому что не будет выполняться условие Фано):
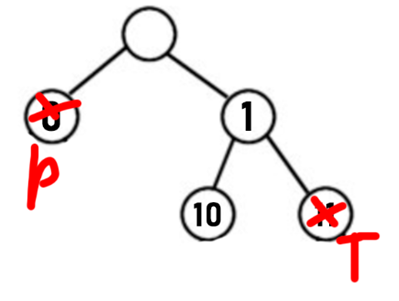
2. Считаем количество оставшихся букв (А, В, И, Н) в слове ИНВАРИАНТ: А встречается 2 раза, В – 1 раз, И – 2 раза, и Н – тоже 2 раза.
3. У нас есть 2 варианта, как минимально закодировать нужные буквы:
1) Продолжить «100» и «101»:
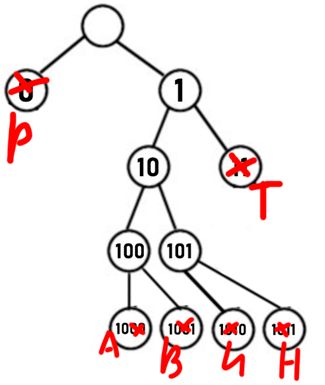
2) Зафиксировать «100» и продолжать «101», «1010» присваиваем любой букве кроме В, т.к. В встречается реже всего в слове:
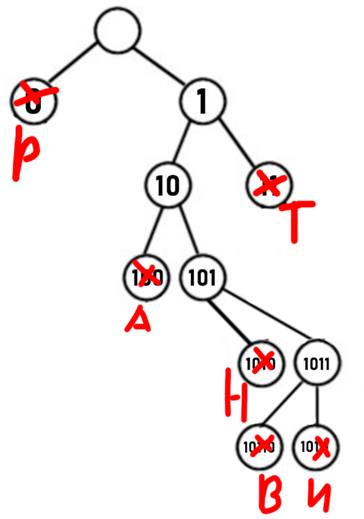
Посчитаем сумму в каждом варианте: 1) 2*4 + 1*4 + 2*4 + 2*4 = 28; 2) 2*3 + 2*4 + 1*5 + 2*5 = 29, значит выбираем первый вариант, поскольку он лучше.
4. Считаем сумму двоичных знаков для слова ИНВАРИАНТ: 28 + 1*1 + 1*2 = 31 (по условию Р закодировано «0», а Т – «11»)
Ответ: 31
Нужно понимать, что 4я задача ЕГЭ по информатике является задачей базового уровня, она не должна занимать много времени и быть слишком сложной. Все прототипы, которые мы разобрали за разные года не сильно отличаются, нужно просто внимательно читать условие, понимать, что от вас хотят составители. Попробуйте решить задачу двумя способами: аналитически (подбором кодов) и через бинарное дерево. Это поможет убедиться в правильности ответа. Ещё один очень важный момент.
В задаче может быть сказано, что кодируются все буквы русского алфавита, а посчитать нужно сумму знаков для какого-то слова, тогда нам нужно будет просто оставить один свободный узел!
Потому что его можно будет продолжать и кодировать оставшиеся буквы алфавита.
Если в задании нужно кодировать конкретное слово, начните с анализа частот появления букв. Для минимального числа двоичных знаков наиболее часто встречающиеся символы нужно кодировать самыми короткими кодами.
Помните, что по условию Фано ни одно кодовое слово не должно быть префиксом другого. Это поможет исключить неподходящие варианты, особенно когда рассматриваются короткие коды.
Удачи на экзамене!
В варианте ЕГЭ-2025 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
