Задача 8 в ЕГЭ по информатике проверяет учеников на знание основ комбинаторики. В нем вам предстоит находить количество всевозможных последовательностей и находить определенные слова.
Для успешного выполнения этой задачи необходимо понимать комбинаторику, знать несколько математических формул и разбираться в библиотеке itertools на питоне.
Давайте разберем основные термины и понятия
Комбинаторика — раздел математики, посвящённый решению задач, связанных с выбором и расположением элементов некоторого множества. Мы будем очень часто возвращаться к законам и формулам из комбинаторики.
Давайте разберем простую задачу из комбинаторики: есть трехзначный код, цифры в котором не могут повторяться, нужно найти количество всевозможных кодов. На первом месте может находиться одна цифра из 10. Так как цифры не повторяются, на втором месте только одна из 9, а на третьем – одна из 8. Количество всевозможных кодов – перемноженное количество возможных цифр на каждом месте = 10 * 9 * 8 = 720.
Теперь давайте разберем три формулы комбинаторики, которые мы будем использовать.
Формулы перестановки, размещения и сочетания используются в комбинаторике для расчета различных комбинаций объектов.
1. Перестановка
Перестановка – это расположение всех элементов множества в определённом порядке. Если у нас есть n различных элементов, то количество возможных перестановок из этих элементов обозначается как Pn и рассчитывается по формуле:
\(P_{n}=n!\)
где n! (факториал n) – это произведение всех чисел от 1 до n.
Для множества из трёх элементов {A, B, C} возможные перестановки: ABC, ACB, BAC, BCA, CAB, CBA. Всего 3! = 6 перестановок.
2. Размещение
Размещение – это расположение некоторых элементов множества в определённом порядке. Если у нас есть n различных элементов и мы выбираем k элементов для размещения, то количество возможных размещений обозначается как \(A_{n}^{k}\) и рассчитывается по формуле:
\(A_{n}^{k}=\frac{n!}{(n-k)!}\)
Пусть у нас есть множество из трёх элементов {A, B, C}, и мы выбираем два элемента для размещения. Возможные размещения: AB, AC, BA, BC, CA, CB. Всего \(A_{3}^{2}=\frac{3!}{(3-2)!}=6\) размещений.
3. Сочетание
Сочетание – это выбор некоторых элементов множества без учёта порядка. Если у нас есть n различных элементов и мы выбираем k элементов, то количество сочетаний обозначается как \(C_{n}^{k}\) и рассчитывается по формуле: \(C_{n}^{k}=\frac{n!}{k!(n-k)!}\)
Пусть у нас есть множество из трёх элементов {A, B, C}, и мы выбираем два элемента. Возможные сочетания: AB, AC, BC. Всего \(C_{3}^{2}=\frac{3!}{2!(3-2)!}=3\) сочетания.
Эти формулы помогут рассчитать, сколько существует возможных способов упорядочить или выбрать элементы из множества в зависимости от условий задачи.
Теперь давайте разберем библиотеку itertools и все нужные функции для 8 задания.
Чтобы использовать функции из библиотеки, необходимо в самом начале python файла написать from itertools import *
1. permutations()
Функция permutations генерирует все возможные перестановки из элементов последовательности. Можно указать количество элементов для перестановки. Если это значение не указано, берётся вся последовательность. Это аналог формул перестановки и размещения. Используется в случаях, когда каждый символ используется 1 раз и порядок символов важен.
permutations(iterable, r)
iterable — последовательность (например, список или строка).
r — длина перестановки.
Пример:
list(permutations([1, 2, 3]))
Результат: [(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]
2. product
Функция product генерирует все возможные перестановки из элементов последовательности, причем элементы могут повторяться. Нужно указать количество элементов для перестановки. Используется в случаях, когда каждый символ используется любое количество раз и порядок символов важен.
product(iterable, repeat=r)
iterable — несколько последовательностей.
r — число повторений.
Пример:
list(product([1, 2, 3], repeat=2))
Результат: [(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]
3. combinations
Функция combinations генерирует уникальные комбинации элементов из последовательности. Порядок элементов не имеет значения, а один и тот же элемент не используется повторно. Аналог формулы сочетаний. Используется в случаях, когда каждый символ используется 1 раз и порядок символов не важен.
combinations(iterable, r)
iterable — последовательность.
r — количество элементов в комбинации.
Пример:
list(combinations([1, 2, 3], 2))
Результат: [(1, 2), (1, 3), (2, 3)]
Этих знаний нам хватит, чтобы решать 8 задание.
Общий алгоритм действий при решении 8 задания
Примеры:
Демоверсия 2025
Определите количество 12-ичных пятизначных чисел, в записи которых ровно одна цифра 7 и не более трёх цифр с числовым значением, превышающим 8.
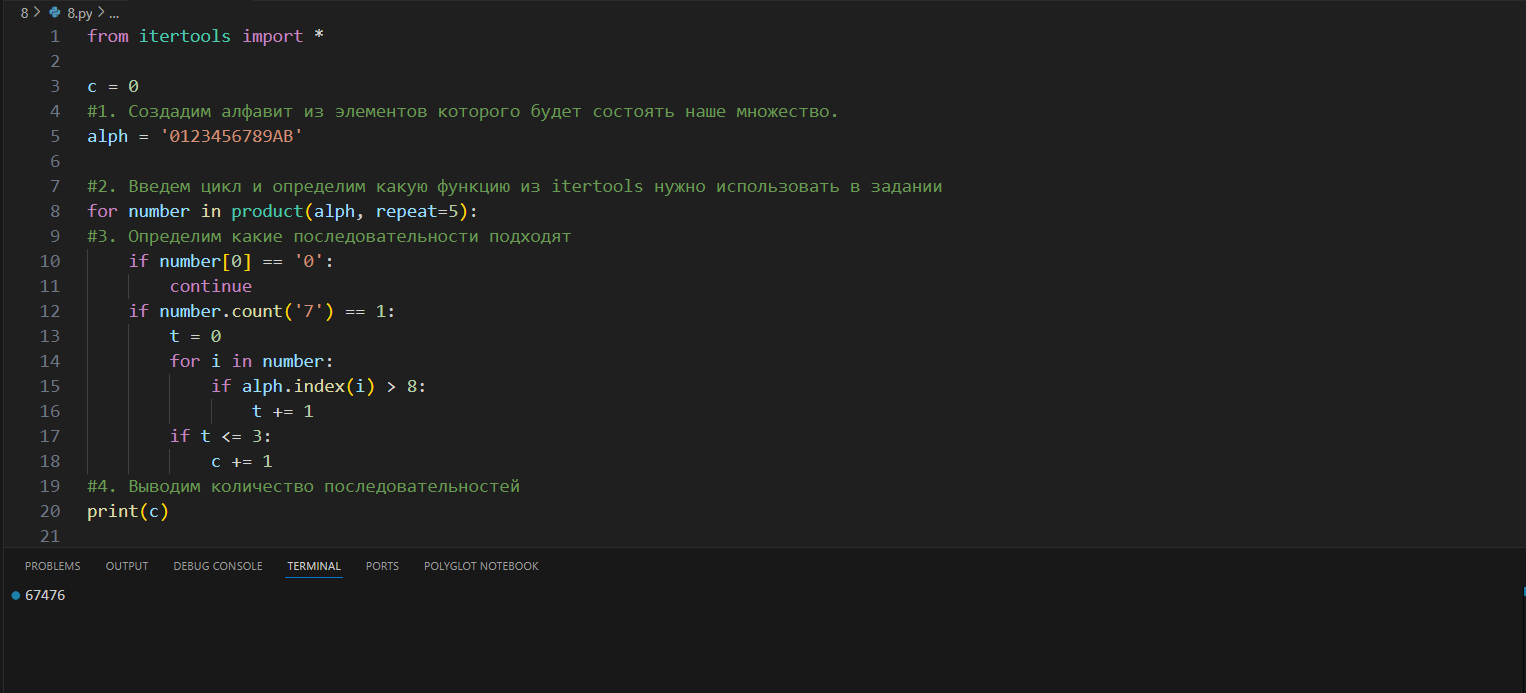
2. ЕГКР 27.04.24
Сколько существует семизначных семеричных чисел, которые содержат в своей записи ровно две чётные цифры?
1. Создадим алфавит из элементов, из которых будет состоять наше множество Алфавит (цифры семеричной системы счисления): 0, 1, 2, 3, 4, 5, 6
2. Введем цикл и определим, какую функцию нужно использовать в задании
Для определения количества способов выбора позиций для чётных цифр будем использовать функцию сочетаний C(n, k), которая вычисляет количество способов выбрать k элементов из n без учёта порядка.
Нам нужно выбрать позиции для двух чётных цифр в семизначном числе.
3. Определим какие последовательности подходят
Рассмотрим два случая:
Случай 1: Первая цифра является чётной.
Случай 2: Первая цифра является нечётной.
4. Выводим количество последовательностей
Общее количество допустимых семизначных семеричных чисел:
17496 + 58320 = 75816
Существует 75816 семизначных семеричных чисел, содержащих ровно две чётные цифры.
3. Досрочная волна 2024
Все 5-буквенные слова, в составе которых могут быть только буквы П, А, Р, У, С, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
Под каким номером в списке идёт первое слово, которое содержит не более одной буквы У и не содержит букв А, стоящих рядом?
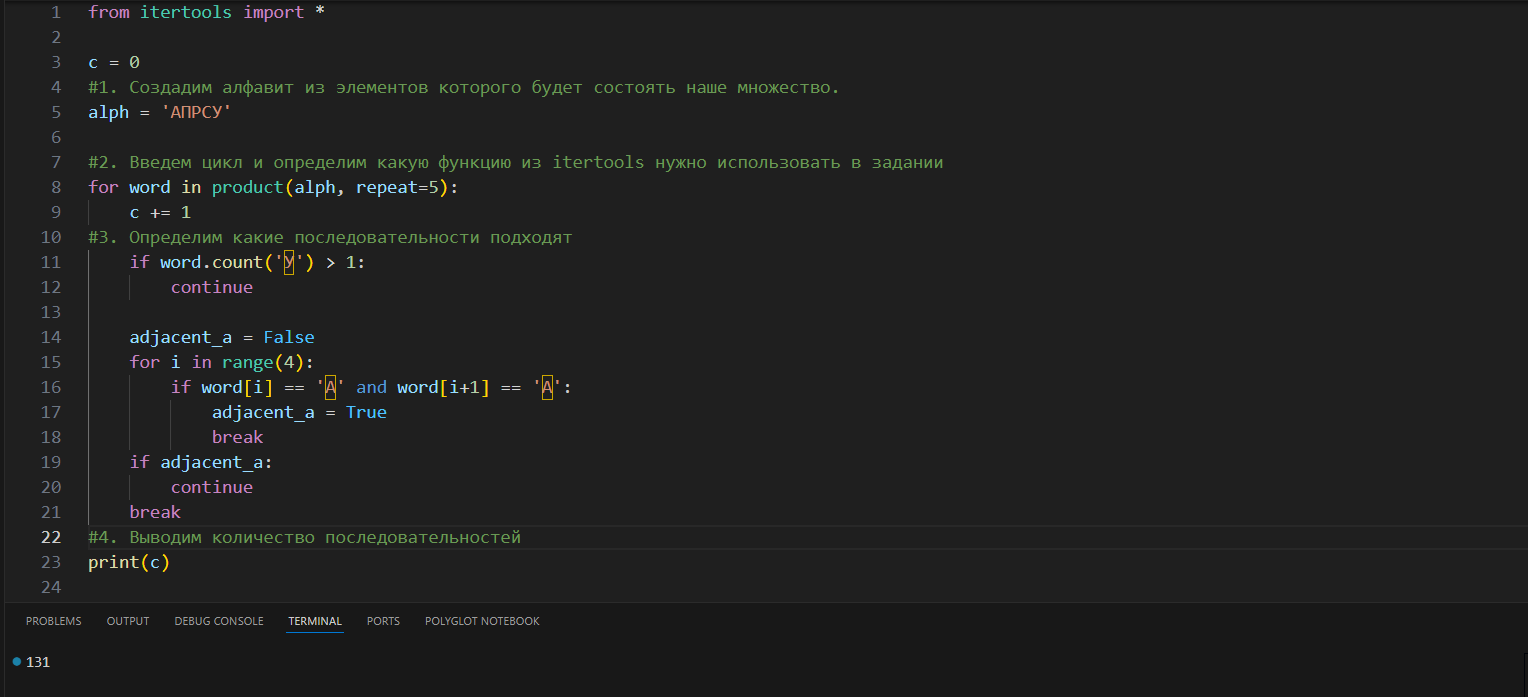
4. № 1941
Лиля составляет пятибуквенные слова из букв С, О, Т, К, А, П, Л, З. Слово не должно заканчиваться на гласную и содержать сочетания ЗЛО. Буквы в слове не повторяются. Сколько слов может составить Лиля?
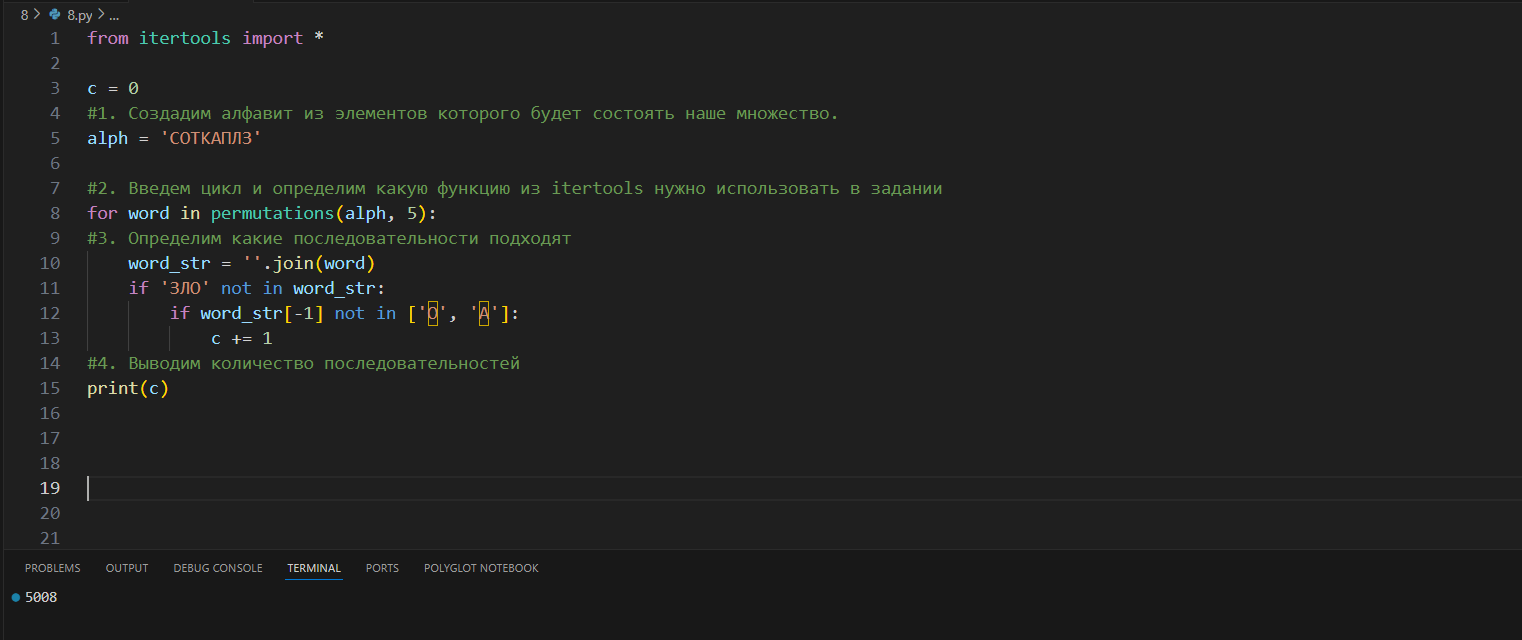
5. Основная волна 2023 I
Все шестибуквенные слова, составленные из букв М, А, Н, Г, У, С, Т, записаны в алфавитном порядке и пронумерованы.
Вот начало начала списка:
Под каким номером в списке стоит последнее слово, которое не начинается с буквы У, содержит только две буквы М и не более одной буквы Г
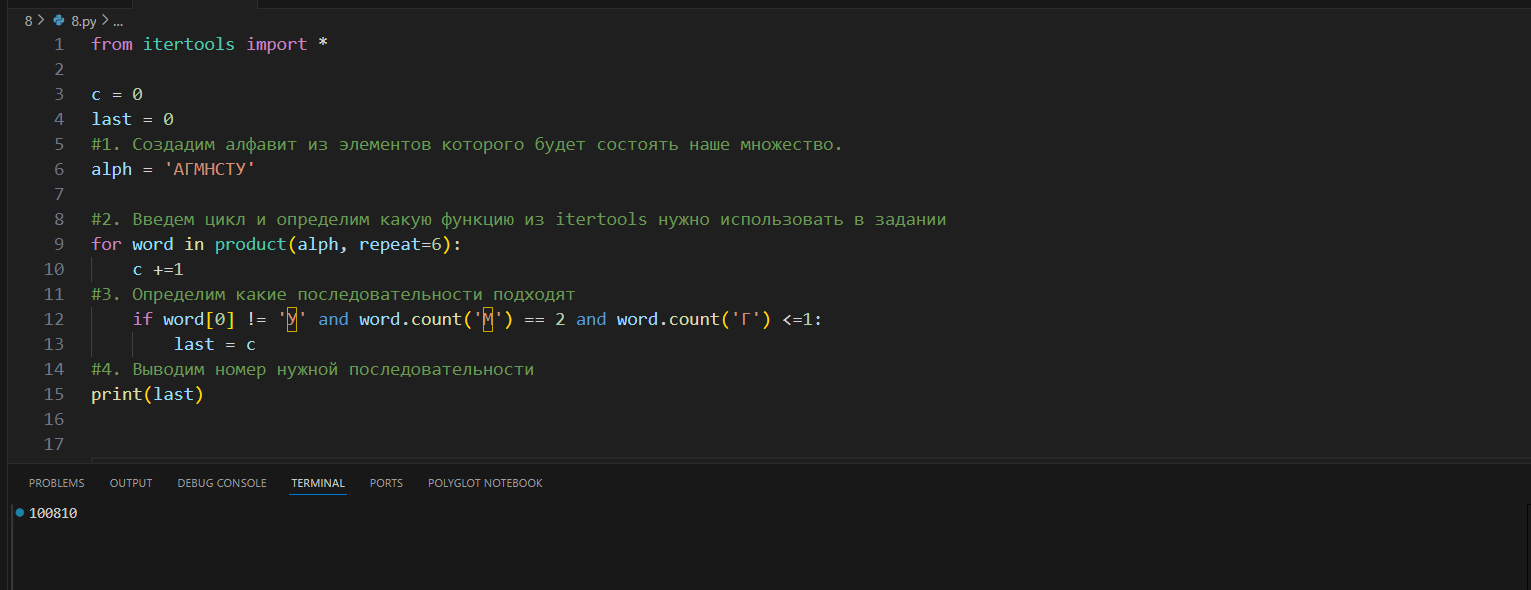
6. Основная волна 2023 II
"Все пятибуквенные слова, составленные из букв К, О, М, П, Ь, Ю, Т, Е, Р, записаны в алфавитном порядке и пронумерованы.
Вот начало списка:
Под каким номером в списке стоит последнее слово с нечётным номером, которое не начинается с буквы Ь и содержит ровно две буквы К?
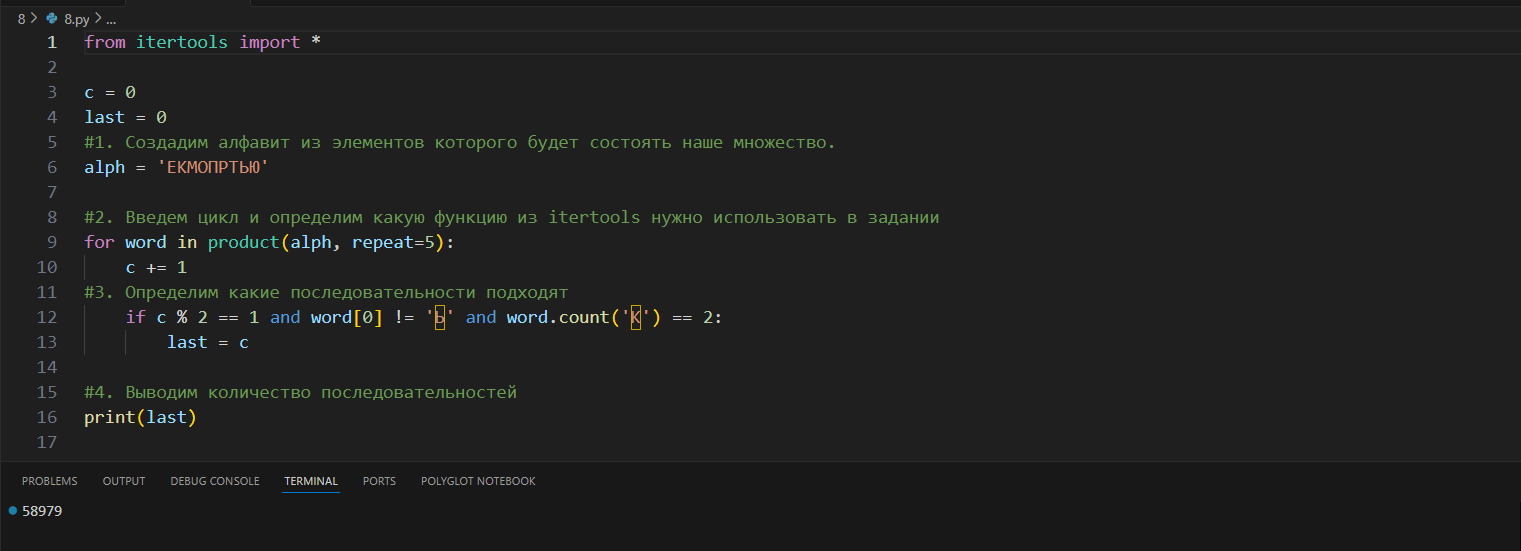
7. Пробник 09.2022
Определите количество пятизначных чисел, записанных в девятеричной системе счисления, которые не начинаются с нечётных цифр, не оканчиваются цифрами 1 или 8, а также содержат в своей записи не более одной цифры 3
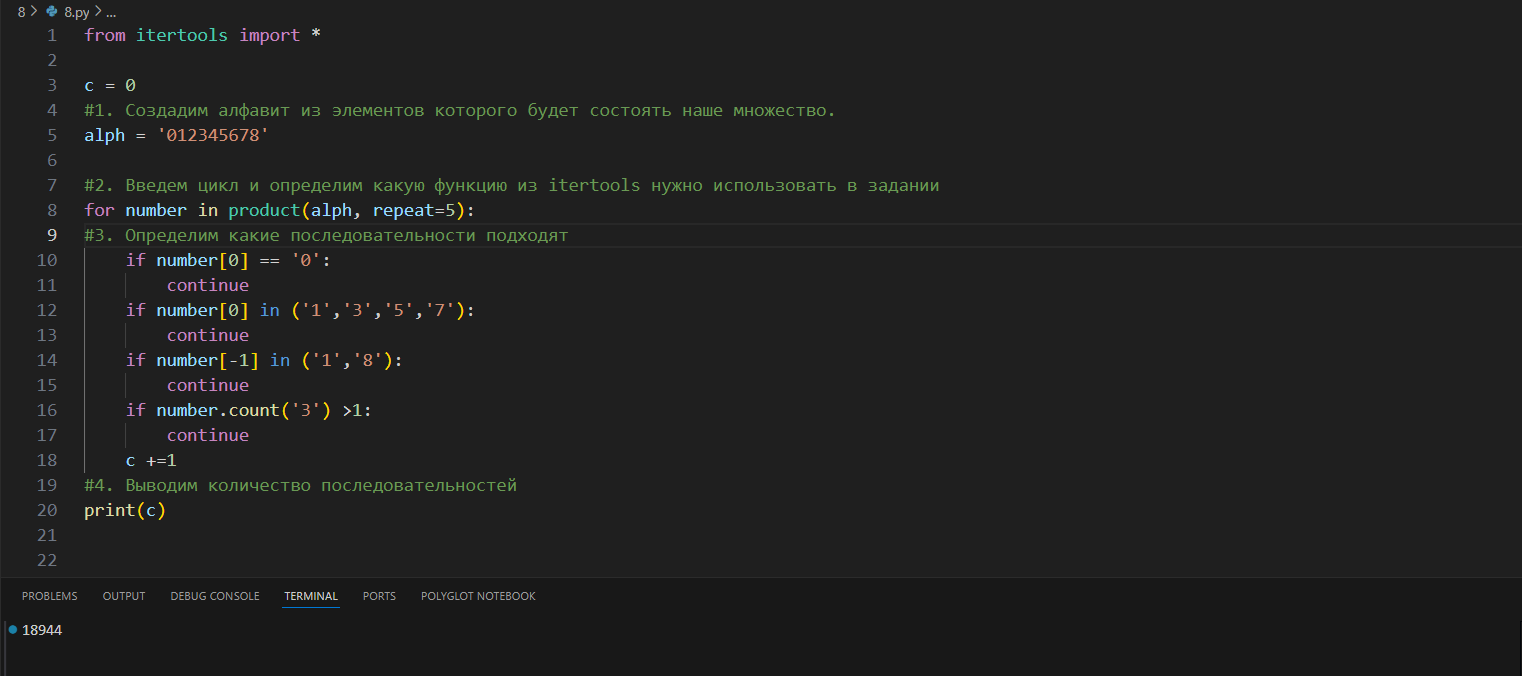
8. Досрочная волна I 2023
Все четырехбуквенные слова, в составе которых могут быть только русские буквы А, В, Л, О, Р записаны в алфавитном порядке и пронумерованы начиная с 1. Ниже приведено начало списка.
Под каким номером идет первое слово, начинающееся на Л?
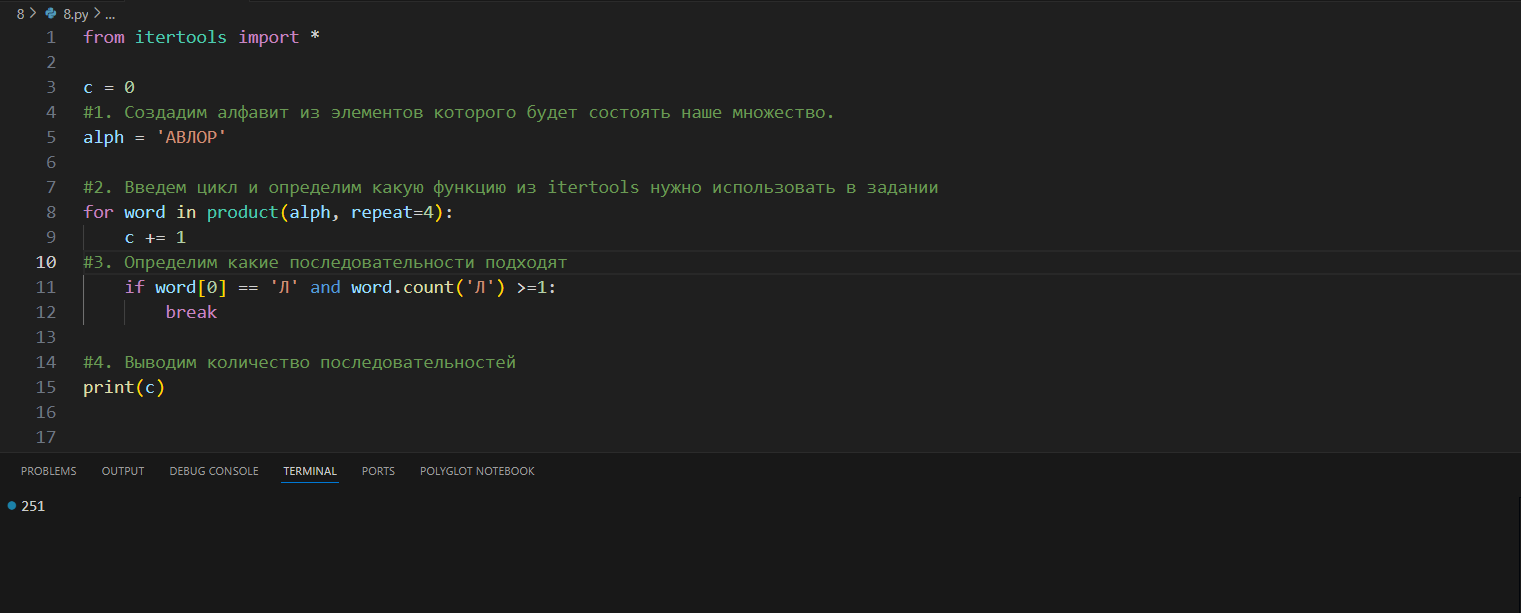
9. Основная волна 07.06.2024
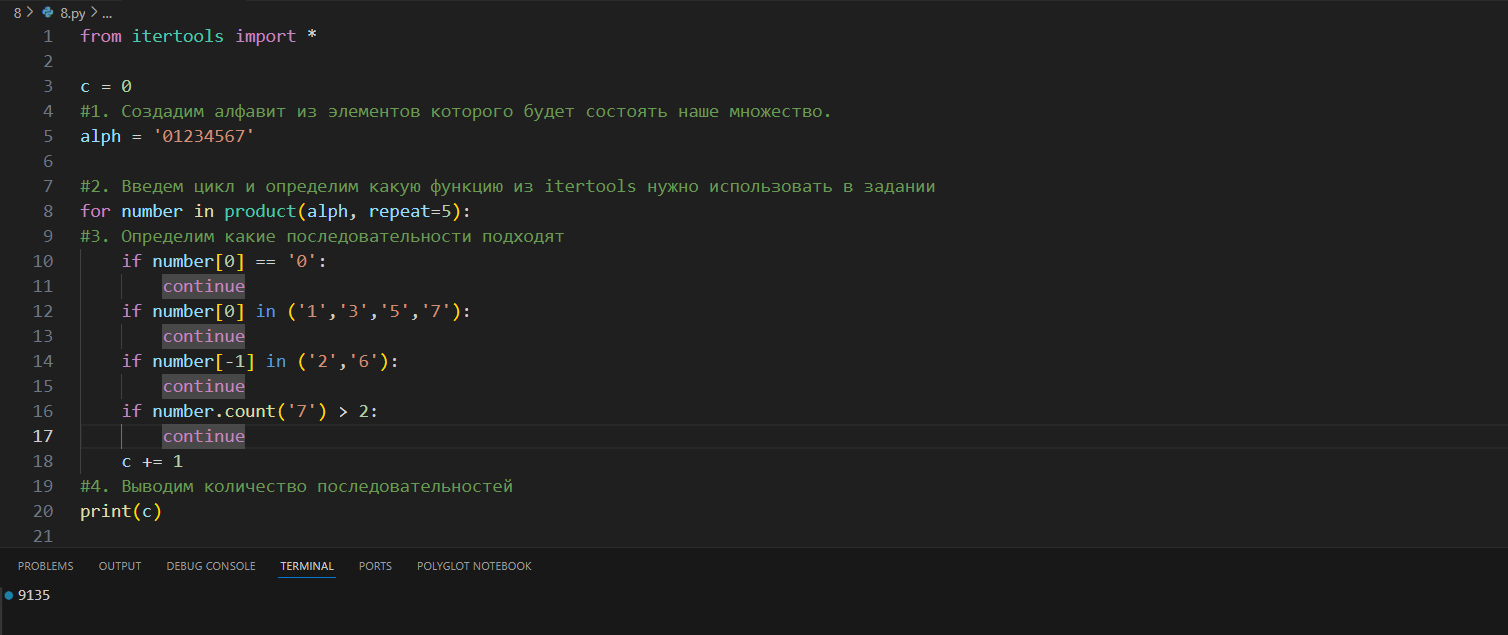
Определите количество восьмеричных пятизначных чисел, которые не начинаются с нечётных цифр, не оканчиваются цифрами 2 или 6, а также содержат не более двух цифр
7.
Для успешного решения задачи 8 на ЕГЭ по информатике важно внимательно читать условия, правильно применять формулы комбинаторики (перестановки, размещения, сочетания) и использовать библиотеку itertools в Python.
Подберите правильную функцию (permutations, product, combinations) в зависимости от условий задачи: если порядок элементов важен, используйте permutations или product, если нет — combinations.
Создайте алфавит из разрешенных элементов и используйте фильтрацию для отбора подходящих последовательностей, избегая лишних вычислений.
Удачи на экзамене!
В варианте ЕГЭ-2025 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
