Задание 13. Решение

а) Решите уравнение: \(3tg^{2}x-\displaystyle \frac{5}{cosx}+5=0.\)

б) Найдите все корни этого уравнения, принадлежащие отрезку \(\Big[-3\pi ;-\displaystyle \frac{3\pi }{2}\Big]. \)

Решение:

ОДЗ: \(cosx\neq 0.\)

а) \(3\displaystyle \frac{sin^{2}x}{cos^{2}x}-\frac{5}{cosx}+5=0.\)

По основному тригонометрическому тождеству \(sin^{2}x=1-cos^{2}x\) получим:

\(3\displaystyle \frac{1-cos^{2}x}{cos^{2}x}-\frac{5}{cosx}+5=0\Leftrightarrow \frac{3}{cos^{2}x}-3-\frac{5}{cosx}+5=0 \Leftrightarrow\)

\(\Leftrightarrow \displaystyle \frac{3}{cos^{2}x}-\frac{5}{cosx}+2=0\Leftrightarrow \left\{\begin{matrix}
cosx\neq 0, \\2cos^{2}x-5cosx+3=0.
\end{matrix}\right.\)

Замена: \(cosx=t, \; \left | t\right |\leq 1.\)

\(2t^{2}-5t+3=0.\)

\(t_{1}=\displaystyle \frac{3}{2}> 1\) - не подходит.

\(t_{2}= 1; \; x=2\pi n, \ n\in Z.\)

б) Выполним отбор корней с помощью единичной окружности. Для этого отметим на единичной окружности отрезок \(\Big[-3\pi ;-\displaystyle \frac{3\pi }{2}\Big]\) и найденную серию решений.

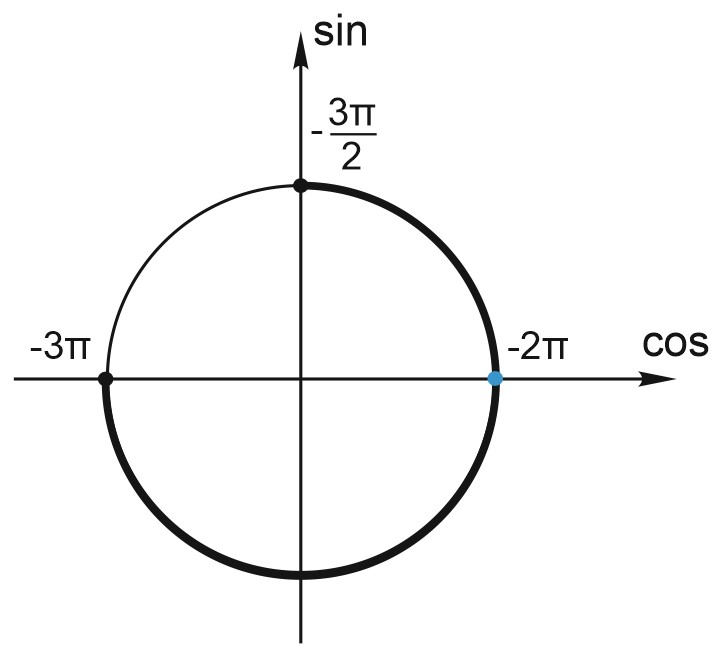
Видим, что данному отрезку принадлежит точка \(-2\pi .\)

Ответ: а) \(2\pi n, \ n\in Z; \; -2\pi .\)