Задание 14. Решение

Основанием четырехугольной пирамиды \(SABCD\) является прямоугольник со сторонами \(AB=24\) и \(BC=7.\) Боковые ребра \(SA= \sqrt{51}, \; SB=\sqrt{627}\) и \(SD=10.\)

а) Докажите, что \(SA\) - высота пирамиды.

б) Найдите угол между прямыми \(SC\) и \(BD.\)

Решение:

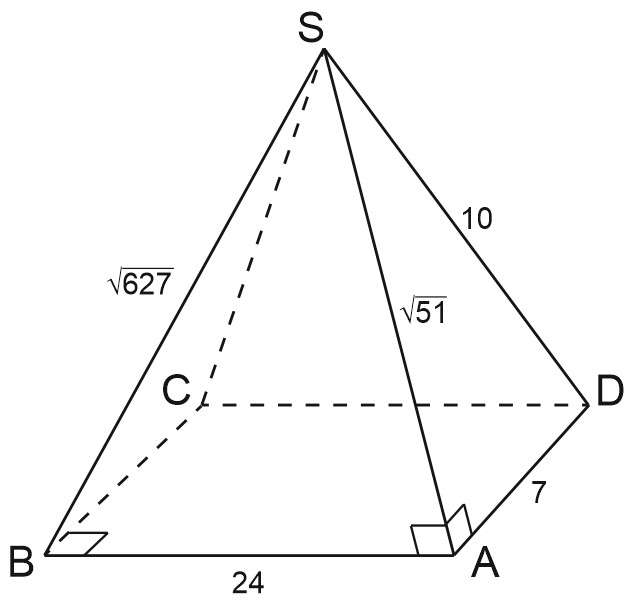
а) В \(\triangle SAD: \; SA^{2}=51, \; AD^{2}=49; \; SD^{2}=100=SA^{2}+AD^{2}\Rightarrow \angle SAD=90^{\circ}\) (выполняется теореме Пифагора).

В \(\triangle SAB: \; SA^{2}=51, \; AB^{2}=576; \; SB^{2}=627=SA^{2}+AB^{2}\Rightarrow \angle SAB=90^{\circ}\) (выполняется теореме Пифагора).

\(SA\perp AD, \; SA\perp AB \Rightarrow SA\perp (ABD)\) - по признаку перпендикулярности прямой и плоскости, чтд.

б) Найдем угол между \(SC\) и \(BD.\)

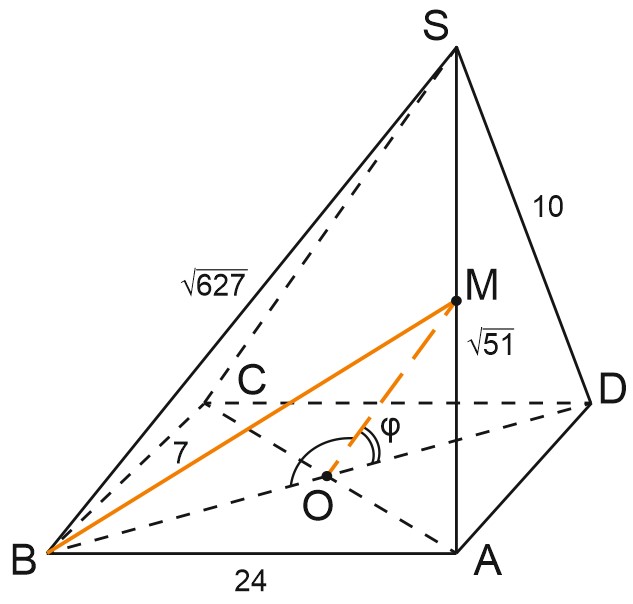
В \(\triangle SAC: \; \angle A=90^{\circ}; \; SC^{2}=625+51=676=26^{2}; \; SC=26.\)

\(BD\cap AC=O, \; M\) - середина \(SA.\)

Тогда \(OM\) - средняя линия \(\triangle SAC, \; OM=\displaystyle \frac{1}{2}CS=13.\)

Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Найдем угол между \(OM\) и \(BD.\)

Из \(\triangle ABM\) по теореме Пифагора: \(BM=\displaystyle \frac{\sqrt{2355}}{2}.\)

Из \(\triangle BOM\) по теореме косинусов \(BM^{2}=OB^{2}+OM^{2}-2 \cdot OB\cdot OM\cdot cos\angle BOM; \)

\(cos\angle BOM=-\displaystyle \frac{527}{650}\) - угол тупой.

Угол между прямыми берем смежный с ним \(\varphi =180^{\circ}-\angle BOM;\)

\(cos\varphi=\displaystyle \frac{527}{650}; \; \varphi=arccos\frac{527}{650}.\)

Ответ: б) \(arccos \displaystyle \frac{527}{650}.\)