Задание 15. Решение

Решите неравенство: \(\displaystyle \frac{log_{5}(5x-27)}{log_{5}(x-5)}\geq 1.\)

Решение:

I способ. Метод рационализации (замены множителя).

\(\displaystyle \frac{log_{5}(5x-27)-log_{5}(x-5)}{log_{5}(x-5)}\geq 0.\)

По методу рационализации:

\(log_{h}f\) заменяем на \((h-1)(f-1); \)

\(log_{h}f-log_{h}g\) заменяем на \((h-1)(f-g).\)

Неравенство равносильно системе:

\(\left\{\begin{matrix} \displaystyle \frac{4(5x-27-x+5)}{4(x-6)}\geq 0, \\5x-27> 0, \\x-5> 0; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \displaystyle \frac{4x-22}{x-6}\geq 0, \\x> \displaystyle\frac{27}{5}, \\x> 5; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \displaystyle \frac{2x-11}{x-6}\geq 0, \\x> \displaystyle\frac{27}{5}, \\x> 5. \end{matrix}\right.\)

Сравним \(\displaystyle \frac{27}{5}=5,4\) и \(\displaystyle \frac{11}{2}=5,5.\)

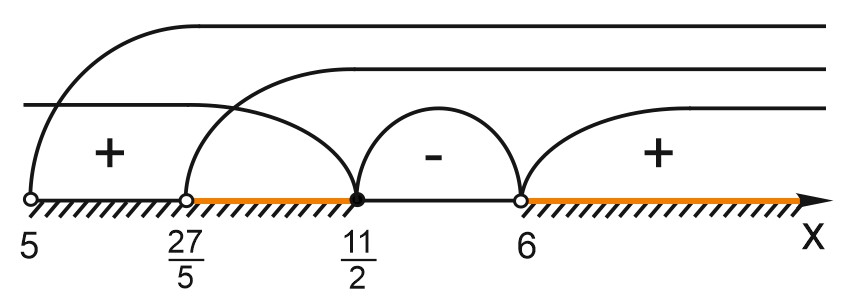
Ответ: \(\Big (\displaystyle \frac{27}{5}; \frac{11}{2}\Big ]\cup (6; +\infty ).\)

II способ.

ОДЗ: \(\left\{\begin{matrix} x> \displaystyle \frac{27}{5}, \\x> 5, \\log_{5}(x-5)\neq 0; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x> \displaystyle \frac{27}{5}, \\x> 5, \\x\neq 6. \end{matrix}\right.\)

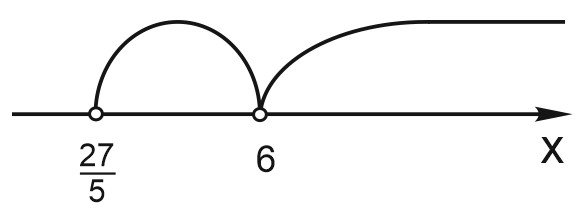
1) \(\displaystyle \frac{27}{5}< x< 6;\)

\(x< 6;\)

\(x-5< 1,\) тогда \(\log_{5}(x-5)< \log_{5}1;\)

\(\log_{5}(x-5)<0,\) тогда \(\displaystyle \frac{log_{5}(5x-27)}{log_{5}(x-5)}\geq 1 \Leftrightarrow \left\{\begin{matrix} \displaystyle \frac{27}{5}< x< 6, \\log_{5}(5x-27)\leq log_{5}(x-5). \end{matrix}\right.\)

Функция \(y= \log_{5}x\) монотонно возрастает, поэтому \(\log_{5}x_{1}< \log_{5}x_{2}\Leftrightarrow x_{1}< x_{2}\) при

\(x_{1}>0, \; x_{2}>0 \Leftrightarrow \left\{\begin{matrix} \displaystyle \frac{27}{5}< x < 6,\\5x-27\leq x-5; \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} \displaystyle \frac{27}{5}< x < 6,\\4x\leq 22. \end{matrix}\right.\)

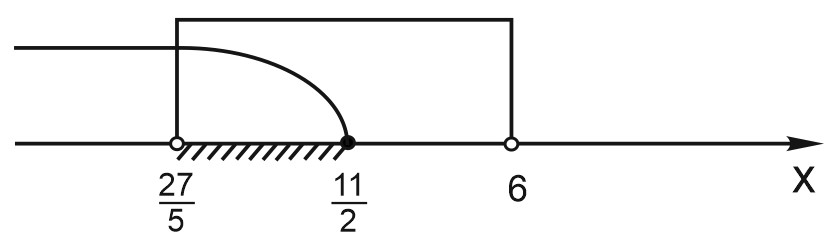
2) \(x>6.\)

\(x-5>1,\) тогда \(\log_{5}(x-5)> \log_{5}1;\)

\(\log_{5}(x-5)>0,\) тогда \(\displaystyle \frac{log_{5}(5x-27)}{log_{5}(x-5)}\geq 1 \Leftrightarrow \left\{\begin{matrix} x> 6, \\log_{5}(5x-27)\geq log_{5}(x-5); \end{matrix}\right.\Leftrightarrow\)

\(\Leftrightarrow \left\{\begin{matrix} x> 6, \\5x-27\geq x-5; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x> 6, \\4x\geq 22; \end{matrix}\right.\Leftrightarrow x> 6.\)

Ответ: \(\Big (\displaystyle \frac{27}{5}; \frac{11}{2}\Big ]\cup (6; +\infty ).\)