Задание 17. Решение

В остроугольном треугольнике \(ABC\) проведены высоты \(AK\) и \(CM.\) На них из точек \(M\) и \(K\) опущены перпендикуляры \(ME\) и \(KH\) соответственно.

а) Докажите, что прямые \(EH\) и \(AC\) параллельны.

б) Найдите отношение \(EH\) и \(AC,\) если \(\angle ABC=60^{\circ}.\)

Решение:

а) Докажем, что \(EH\parallel AC.\)

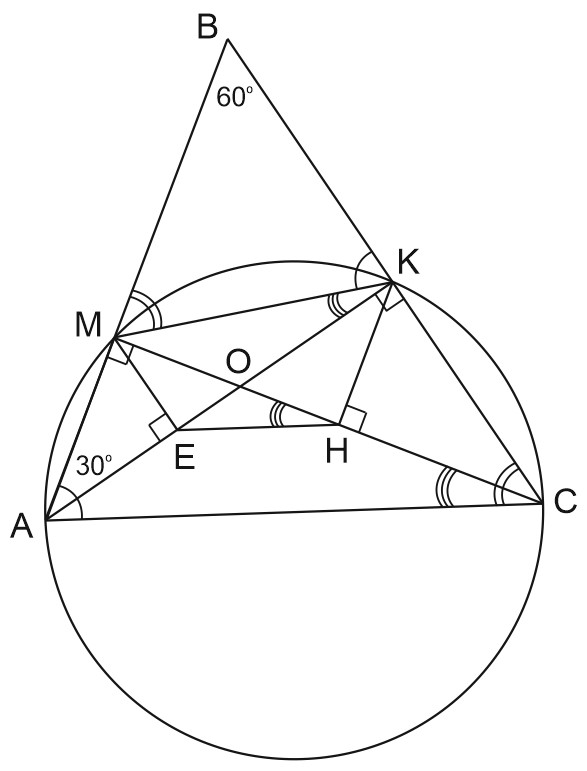
\(\triangle ABK\sim \triangle CBM\) - по двум углам, тогда \(\displaystyle \frac{AB}{BC}=\frac{BK}{MB}\Rightarrow \frac{BK}{AB}=\frac{MB}{BC}=cos\angle B.\)

Тогда \(\triangle MBK\sim \triangle CBA\) (по двум пропорциональным сторонам и углу между ними).

Тогда \(\angle BMK=\angle BCA,\) но \(\angle BMK+\angle KMA=180^{\circ}\Rightarrow \angle BCA +\angle KMA=180^{\circ}\Rightarrow\) четырехугольник \(AMKC\) можно вписать в окружность.

Тогда \(\angle AKM=\angle ACM\) - вписанные, опираются на \(\breve{AM}.\)

В треугольнике \(MKHE: \; \angle MEK=\angle MHK=90^{\circ}.\)

Тогда отрезку \(MK\) виден из точек \(E\) и \(H\) под прямым углом \(\Rightarrow MKHE\) - вписанный в окружность, \(MK\) - диаметр.

Тогда \(\angle MKE=\angle MHE\) - вписанные, опираются на \(\breve{ME}.\)

Тогда \(\angle MCA=\angle MHE\) - соответственные при двух прямых \(EH\) и \(AC\) и секущей \(MC \Rightarrow EH\parallel AC,\) чтд.

б) Найдем \(\displaystyle \frac{EH}{AC},\) если \(\angle ABC=60^{\circ}.\)

Т. к. \(\triangle MBK\sim \triangle CBA\) (из п. (а)), то \(\displaystyle \frac{MK}{AC}=cos\angle B=\frac{1}{2}; \; MK=\frac{1}{2}AC.\)

\(\triangle OEH\sim \triangle OAC\) - по двум углам, тогда \(\displaystyle \frac{EH}{AC}=\frac{OE}{OA}.\)

В \(\triangle OMA: \; \angle MAO=30^{\circ}=\angle OME; \; OE=x,\) тогда \(OM=2x, \; AO=4x.\)

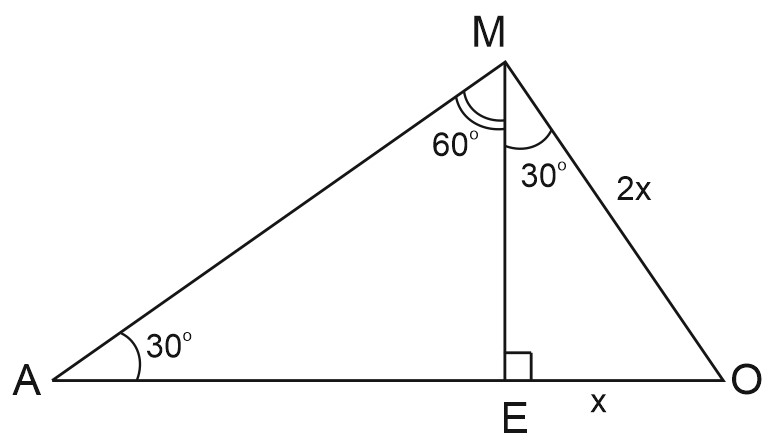
\(\displaystyle \frac{OE}{OA}=\frac{x}{4x}=\frac{1}{4}=\frac{EH}{AC}.\)

Ответ: \(\displaystyle \frac{1}{4}.\)