Задание 18. Решение

Найдите все значения параметра \(a,\) при которых уравнение \((\left | x+2\right |+\left | x-a\right |)^{2}-5(\left | x+2\right |+\left | x-a\right |)+3a(5-3a)=0\) имеет ровно два решения.

Решение:

Сделаем замену: \(\left | x+2\right |+\left | x-a\right |=t.\)

Уравнение примет вид: \(t^{2}-5t+3a(5-3a)=0;\)

\(D=25-4 \cdot 3a(5-3a)=25-60a+36a^{2}=(5-6a)^{2}\geq 0.\)

По теореме Виета: \(t_{1}+t_{2}=5;\)

\(t_{1}\cdot t_{2}=3a(5-3a).\)

Тогда \(t_{1}=3a, \; t_{2}=5-3a.\)

Вернемся к переменной \(x:\)

\(\left[\begin{matrix}
\left | x+2\right |+\left | x-a\right |=3a, \\\left | x+2\right |+\left | x-a\right |=5-3a
\end{matrix}\right.\) - ровно два решения.

Рассмотрим функцию \(y=\left | x+2\right |+\left | x-a\right |\) -  «корыто».

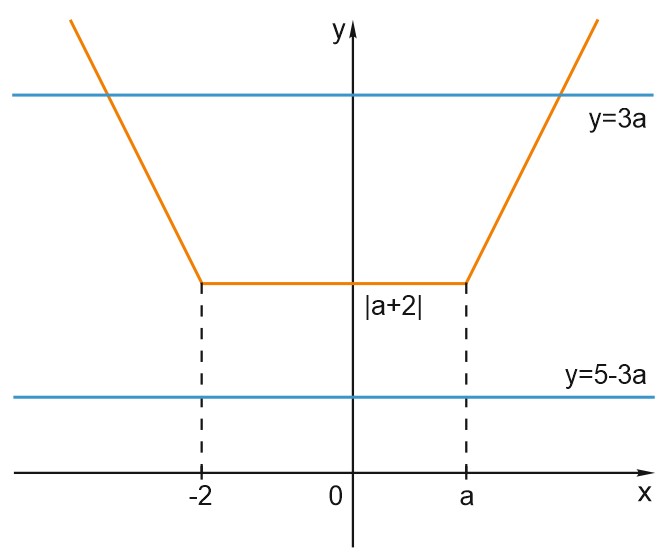
\(y(-2)=\left | a+2\right |=y(a);\)

\(y=3a, \; y=5-3a\) - горизонтальные прямые.

Исходное уравнение имеет два решения в следующих случаях:

1) Случай, когда прямые совпадают:

\(3a=5-3a;\)

\(a=\displaystyle \frac{5}{6};\)

\(y=3a=\displaystyle \frac{5}{2}.\)

Тогда \(\left | a+2\right |=2\displaystyle \frac{5}{6},\) значит, совпадающие прямые не пересекают график функции.

\(y=\left | x+2\right |+\left | x-a\right |\) - нет решений.

2) Случай, когда одна горизонтальная прямая пересекает график:

\(\left\{\begin{matrix} 3a> \left | a+2\right |, \\5-3a< \left | a+2\right | \end{matrix}\right. \; \) или \(\; \left\{\begin{matrix} 3a< \left | a+2\right |, \\5-3a> \left | a+2\right |. \end{matrix}\right.\)

\(\left | A\right |< B\Leftrightarrow -B< A< B;\)

\(\left | A\right |> B\Leftrightarrow\left[\begin{matrix} A> B, \\A< -B. \end{matrix}\right.\)

\( \left\{\begin{matrix} 3a> \left | a+2\right |, \\5-3a< \left | a+2\right |; \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} a+2< 3a, \\a+2> -3a, \\\left[\begin{matrix} a+2> 5-3a, \\a+2< 3a-5; \end{matrix}\right. \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a> 1, \\a> -\displaystyle \frac{1}{2}, \\\left[\begin{matrix} a> \displaystyle \frac{3}{4}, \\a> \displaystyle \frac{7}{2}; \end{matrix}\right. \end{matrix}\right.\Leftrightarrow a> 1.\)

\( \left\{\begin{matrix} 3a< \left | a+2\right |, \\5-3a> \left | a+2\right |; \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} a+2> 3a, \\a+2< -3a, \end{matrix}\right. \\a+2< 5-3a, \\a+2> 3a-5; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} a< 1, \\a< -\displaystyle\frac{1}{2}, \end{matrix}\right. \\a< \displaystyle\frac{3}{4}, \\a< \displaystyle\frac{7}{2} \end{matrix}\right.\Leftrightarrow a< \displaystyle \frac{3}{4}.\)

Ответ: \( \Big(-\infty ;\displaystyle \frac{3}{4}\Big)\cup (1;+\infty ).\)