ЕГЭ-2024. Задание 13. Решение

а) Решите уравнение: \(sin2x+\sqrt{3}sin(x-\pi )=0.\)

б) Найдите все корни этого уравнения, принадлежащие отрезку \(\Big[-\displaystyle \frac{7\pi }{2}; -2\pi \Big].\)

Решение:

а) Применим формулы \(sin2x=2sinxcosx\) и \(sin(x-\pi )=sinxcos\pi -cosxsin\pi =-sinx.\)

Уравнение примет вид:

\(2sinxcosx-\sqrt{3}sinx=0;\)

\(sinx(2cosx-\sqrt{3})=0;\)

\(sinx=0\) или \(cosx=\displaystyle \frac{\sqrt{3}}{2}.\)

\(x=\pi n, \; n\in Z\) или \(x=\pm \displaystyle \frac{\pi}{6}+2\pi k, \; k\in Z.\)

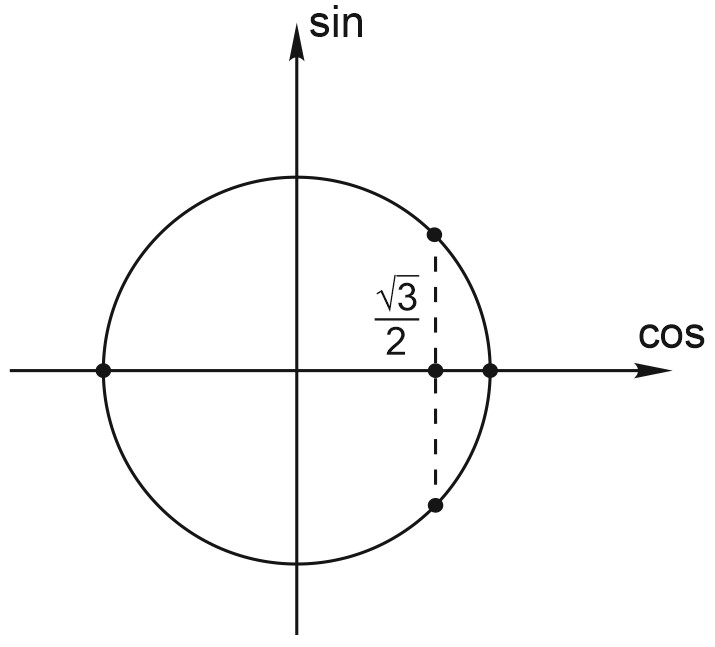
б) Выполним отбор корней на отрезке \(x\in \Big[-\displaystyle \frac{7\pi }{2}; -2\pi \Big]\) с помощью единичной окружности. Отметим на единичной окружности данный отрезок и найденные серии решений.

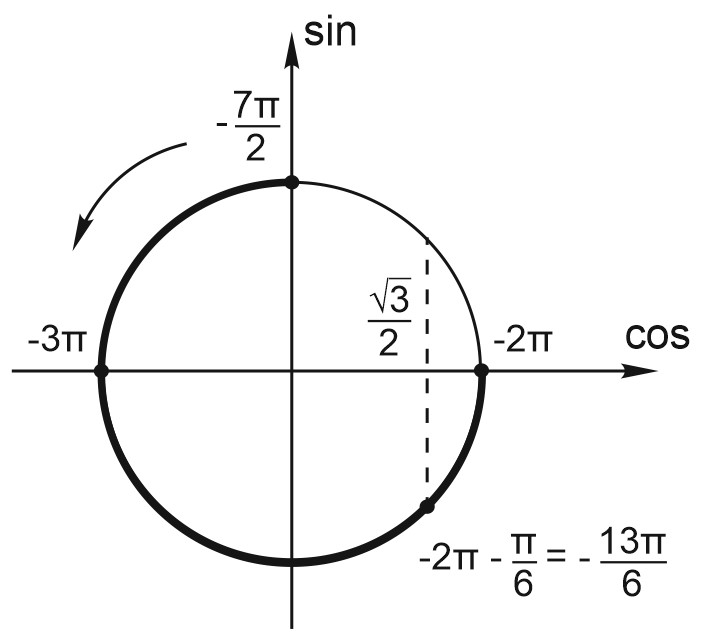
Видим, что указанному отрезку принадлежат точки: \(x_{1}=-3\pi , \; x_{2}=-\displaystyle \frac{13\pi }{6}, \; x_{3}=-2\pi .\)

Ответ: а) \(\pi n; \; \pm \displaystyle \frac{\pi}{6}+2\pi k, \; n, \ k\in Z.\)

б) \(-3\pi ; \; -\displaystyle \frac{13\pi }{6}; \; -2\pi .\)