В правильной треугольной пирамиде \(SABC\) стороны основания \(ABC\) равны 12, а боковые ребра - 25. На ребрах \(AB, \; AC\) и \(SA\) отмечены точки \(F, \; E\) и \(K\) соответственно. Известно, что \(AE=AF=10, \; AK=15.\)
а) Докажите, что объем пирамиды \(KAEF\) составляет \(\displaystyle \frac{5}{12}\) от объема пирамиды \(SABC.\)
б) Найдите площадь сечения пирамиды плоскостью \(KEF.\)
Решение:
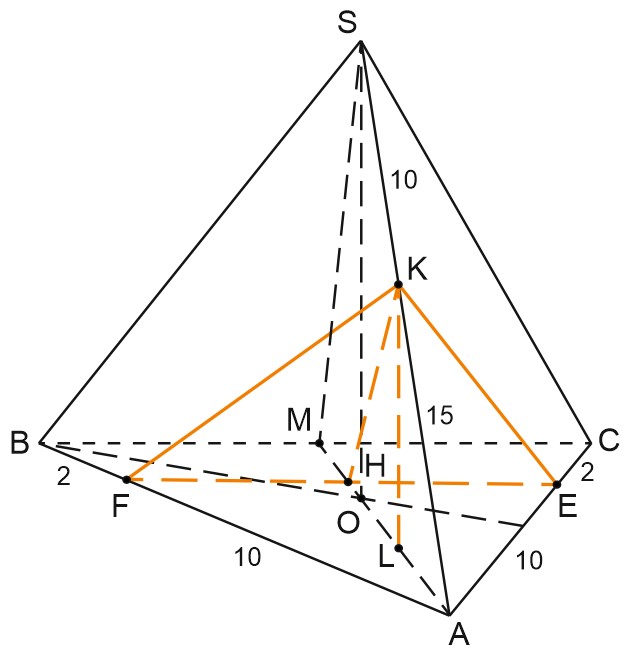
\(\triangle AFE\sim \triangle ABC\) (по углу и двум сторонам).
\(V_{SABC}=\displaystyle \frac{1}{3}S_{\triangle ABC}\cdot SO.\)
\(V_{KAFE}=\displaystyle \frac{1}{3}S_{\triangle AFE}\cdot h.\)
\(L\) - проекция \(K\) на \((ABC), \; KL=h.\)
\(\triangle AFE\sim \triangle ABC, \; k=\displaystyle \frac{AE}{AC}=\frac{5}{6};\)
\(S_{\triangle AEF}=k^{2} \cdot S_{\triangle ABC}=\displaystyle \frac{25}{36}\cdot S_{\triangle ABC}.\)
\(\triangle AKL\sim \triangle ASO\) (по двум углам), \(\displaystyle \frac{KL}{SO}=\frac{AK}{SA}=\frac{15}{25}=\frac{3}{5}; \; KL=\frac{3}{5}SO.\)
\(V_{KAFE}=\displaystyle \frac{1}{3}\cdot \frac{25}{36}\cdot S_{\triangle ABC}\cdot \frac{3}{5}SO=\frac{25}{36}\cdot \frac{3}{5} \cdot V_{SABC} = \frac{5}{12}V_{SABC},\) чтд.
б) Найдем \(S_{\triangle KEF}.\)
\(FE=\displaystyle \frac{5}{6}BC=10.\)
\(\triangle AFK= \triangle AEK\) (по углу и двум сторонам), тогда \(\triangle KEF\) - равнобедренный.
\(AO\cap BC=M.\)
\(AM=\displaystyle \frac{12\sqrt{3}}{2}=6\sqrt{3}\) (высота правильного треугольника).
\(AO=\displaystyle \frac{2}{3}AM=4\sqrt{3}.\)
\(AL=\displaystyle \frac{3}{5}AO=\frac{12}{5}\sqrt{3}\) (из подобия \(\triangle AKL\sim \triangle ASO\)).
\(AL\cap EF=H.\)
\(KH\) - высота \(\triangle KEF, \; S_{\triangle KEF}=\displaystyle \frac{FE\cdot KH}{2}.\)
\(HL=AH-AL; \; AH=\displaystyle \frac{5}{6}AM=5\sqrt{3}; \)
\(HL=AH-AL=5\sqrt{3}-\displaystyle \frac{12}{5}\sqrt{3}=\frac{13}{5}\sqrt{3}.\)
Из \(\triangle SOA\) по теореме Пифагора: \(SO=\sqrt{SA^{2}-OA^{2}}=\sqrt{25^{2}-48}=\sqrt{577}.\)
\(KL=\displaystyle \frac{3}{5}SO=\frac{3}{5}\sqrt{577}.\)
Из \(\triangle KHL\) по теореме Пифагора: \(KH=\sqrt{\Big(\displaystyle \frac{13}{5}\sqrt{3}\Big)^{2}+\Big(\displaystyle \frac{3}{5}\sqrt{577}\Big)^{2}}=2\sqrt{57}.\)
\(S_{\triangle KEF}=\displaystyle \frac{1}{2}\cdot FE \cdot KH=\frac{1}{2}\cdot 10\cdot 2\sqrt{57}=10\sqrt{57}.\)
Ответ: б) \(10\sqrt{57}.\)
В варианте ЕГЭ 2026 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
