ЕГЭ-2024. Задание 15. Решение

Решите неравенство: \(\displaystyle \frac{3^{x}+9}{3^{x}-9}+ \frac{3^{x}-9}{3^{x}+9}\geq \frac{4\cdot 3^{x+1}+144}{9^{x}-81}.\)

Решение:

Сделаем замену: \(3^{x}=t, \; t> 0.\)

Тогда \(3^{x+1}=3\cdot 3^{x}=3t;\)

\(9^{x}=3^{2x}=t^{2}.\)

Уравнение примет вид:

\(\displaystyle \frac{t+9}{t-9}+\frac{t-9}{t+9}\geq \frac{12t+144}{t^{2}-81}\Leftrightarrow \frac{(t+9)^{2}+(t-9)^{2}}{t^{2}-81}-\frac{12t+144}{t^{2}-81}\geq 0\Leftrightarrow\)

\(\Leftrightarrow \displaystyle \frac{2t^{2}+162-12t-144}{t^{2}-81}\geq 0 \Leftrightarrow\frac{2t^{2}-12t+18}{t^{2}-81}\geq 0\Leftrightarrow\)

\(\Leftrightarrow \displaystyle \frac{t^{2}-6t+9}{t^{2}-81}\geq 0\Leftrightarrow \frac{(t-3)^{2}}{(t-9)(t+9)}\geq 0.\)

Так как \(t> 0,\) то \(t+9> 0,\) получим равносильное уравнение: \(\displaystyle \frac{(t-3)^{2}}{(t-9)}\geq 0.\)

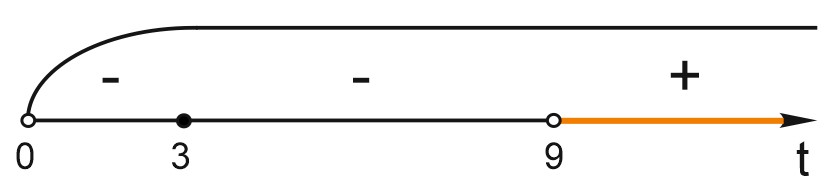
\(t> 9\) или \(t=3.\)

Вернемся к переменной \(x:\)

\(3^{x}> 9\) или \(3^{x}=3;\)

\(3^{x}> 3^{2}\) или \(3^{x}= 3^{1}.\)

Функция \(y=3^{x}\) - монотонно возрастает, если \(3^{x_{1}}> 3^{x_{2}},\) то \(x_{1}> x_{2},\) получим \(x> 2\) или \(x=1.\)

Ответ: \(\begin{Bmatrix} 1\end{Bmatrix}\cup (2; +\infty ).\)