ЕГЭ-2024. Задание 17. Решение
Окружность с центром в точке \(O\) касается сторон угла с вершиной \(N\) в точках \(A\) и \(B\). Отрезок \(BC\) - диаметр этой окружности.
а) Докажите, что прямая \(AC\) параллельна биссектрисе угла \(ANB.\)
б) Найдите \(NO,\) если \(AB=24, \; AC=10.\)
Решение:
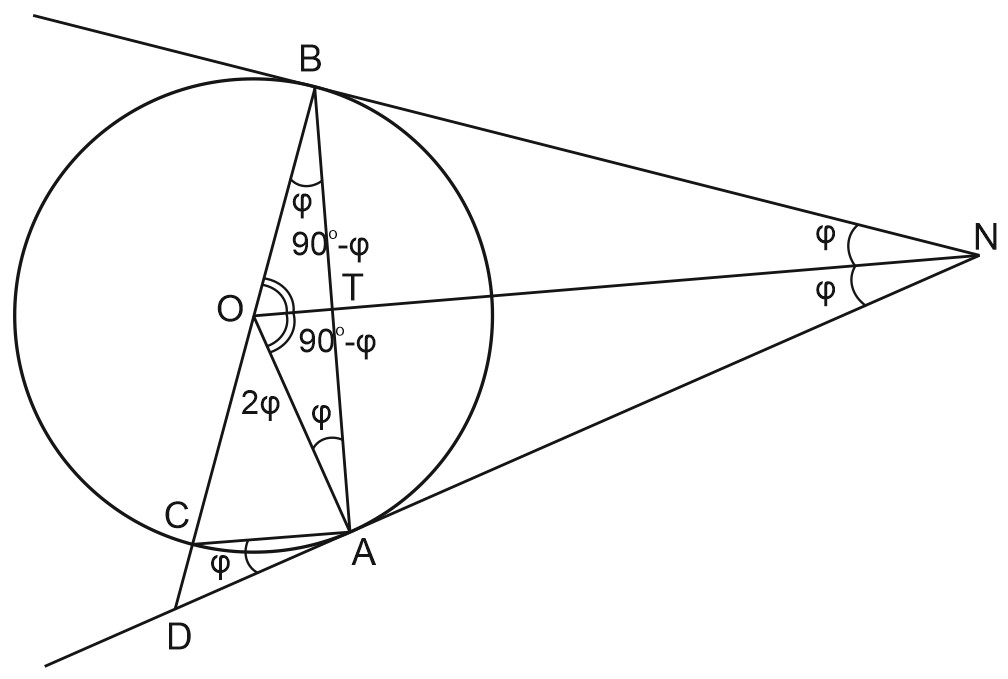
а) Докажем, \(AC \parallel NO.\)
\(NO\) - биссектриса \(\angle ANB\) (т. к. центр окружности, вписанной в угол, лежит на биссектрисе угла).
Так как \(NB\) и \(NA\) - касательные, \(OB\) и \(OA\) - радиусы \(\Rightarrow OB\perp NB, \; OA\perp NA\) (касательная перпендикулярна радиусу, проведенному в точку касания).
\(\varphi =\angle BNO=\angle ANO\) (т. к. \(NO\) - биссектриса).
\(\angle AON=90^{\circ}-\varphi; \; ON\cap AB=T.\)
\(\triangle ANB\) - равнобедренный (\(NB=AN\) - как отрезки касательных).
\(NT\) - биссектриса, медиана и высота \(\triangle ANB\Rightarrow T\) - середина \(AB.\)
\(\triangle AOB\) - равнобедренный \(\Rightarrow \angle OTB=90^{\circ}=\angle OBT=\angle OAT=\varphi.\)
\(\angle ABC=\varphi\) - вписанный угол \(\Rightarrow \angle AOC=2\varphi\) - центральный (опираются на \(\breve{AC}\)).
\(D\in [NA);\)
\(\angle CAD=\varphi\) - угол между касательной и хордой.
\(\angle DAC=\angle DNO\) - соответственные углы \(\Rightarrow AC\parallel NO,\) чтд.
б) Найти \(NO,\) если \(AB=24, \; AC=10\)
\(\triangle ABC\) - прямоугольный, \(\angle A=90^{\circ}\) - опирается на диаметр \(BC.\)
По теореме Пифагора \(BC=26.\)
\(OB=OC=13\) - радиусы; \(T\) - середина \(AB\Rightarrow BT=12.\)
\(\triangle OBT\) - прямоугольный, по теореме Пифагора \(OT=5.\)
Рассмотрим \(\triangle BON\) - прямоугольный, \(\angle B=90^{\circ}, \; BT\) - высота.
\(BT^{2}=OT\cdot NT\) - по свойству высоты, проведенной к гипотенузе.
\(NT=\displaystyle \frac{BT^{2}}{OT}=\frac{144}{5};\)
\(NO=OT+NT=5+\displaystyle \frac{144}{5}=\frac{169}{5}.\)
Ответ: б) \(\displaystyle \frac{169}{5}.\)































