ЕГЭ-2024. Задание 18. Решение

Найдите все значения параметра \(a,\) при каждом из которых система уравнений
\(\left\{\begin{matrix} 2x+2ay+a-3=0, \\x\left | y\right |+2x-3=0 \end{matrix}\right.\) имеет ровно два решения.

Решение:

Решим графически в координатах \((x; y).\)

Первое уравнение: \(2x+2ay+a-3=0;\)

\(2ay=-2x+3-a.\)

Проверим случай, когда \(a=0\) и \(a\neq 0,\) поделим на \(a.\)

Если \(a=0,\) система примет вид: \(\left\{\begin{matrix} x=\displaystyle \frac{3}{2}, \\\displaystyle \frac{3}{2}\left | y\right |=0; \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\displaystyle \frac{3}{2}, \\y=0 \end{matrix}\right.\) - единственное решение, не подходит.

Пусть \(a\neq 0; \; y=-\displaystyle \frac{x}{a}+\frac{3-a}{2a}\) - прямая, угловой коэффициент \(k=-\displaystyle \frac{1}{a}.\) В таком случае у прямой меняется и угловой, и свободный коэффициенты.

Запишем первое уравнение в другой форме:

\(2x=3-a-2ay;\)

\(2x=3-a(1+2y);\)

\(x=-a\Big(y+\displaystyle \frac{1}{2}\Big)+\displaystyle \frac{3}{2}.\)

Если \(y=-\displaystyle \frac{1}{2},\) то \(x=\displaystyle \frac{3}{2}\) для любого \(a.\)

Значит, при любом \(a\) прямая проходит через точку \(M\Big(\displaystyle \frac{3}{2}; -\frac{1}{2}\Big)\) - пучок прямых.

Второе уравнение: \(x\left | y\right |=3-2x. \)

Если \(x=0,\) нет решений. Делим на \(x\neq 0:\)

\(\left | y\right |=\displaystyle \frac{3-2x}{x};\)

\(\left | y\right |=\displaystyle \frac{3}{x}-2.\)

Если \(y\geq 0,\) то \(y=\displaystyle \frac{3}{x}-2\) - гипербола.

Для \(y<0\) - зеркально отразим относительно оси \(X.\)

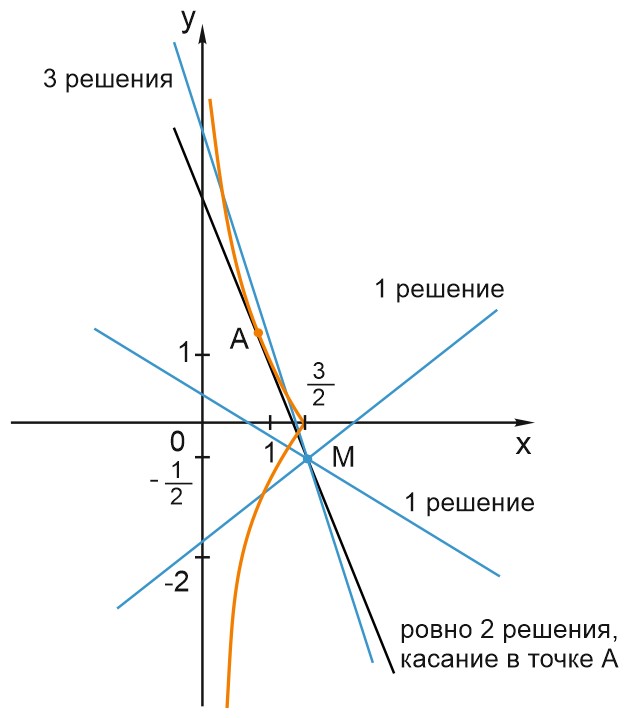
Запишем прямую \(\left | y\right |=-\displaystyle \frac{x}{a}+\frac{3-a}{2a}\) в виде:

\(y=kx+b; \; k=-\displaystyle \frac{1}{a}, \; b=\frac{3-a}{2a}.\)

Проходит через точку \(M\Big(\displaystyle \frac{3}{2}; -\displaystyle \frac{1}{2}\Big).\)

Подставим координаты точки \(M.\) Получим:

\(-\displaystyle \frac{1}{2}=\frac{3}{2}k+b;\)

\(b=-\displaystyle \frac{3k+1}{2};\)

\(y=kx-\displaystyle \frac{3k+1}{2}.\)

Система имеет два решения, когда прямая \(y=-\displaystyle \frac{x}{a}+\frac{3-a}{2a}\) касается графика функции \(\left | y\right |=\displaystyle \frac{3}{x}-2\) в точке \(A.\)

Условие касания \(y=f(x)\) и \(y=kx+b;\)

\( \left\{\begin{matrix}
f(x)=kx+b, \\f'(x)=k.
\end{matrix}\right.\)

Касание в точке \(A\) с верхней ветвью, поэтому \(y> 0.\)

\(\left\{\begin{matrix} \displaystyle \frac{3}{x}-2=kx-\frac{3k+1}{2}, \\-\displaystyle \frac{3}{x^{2}}=k; \end{matrix}\right.\)

\(\displaystyle \frac{6}{x}-2=\frac{9}{2x^{2}}-\frac{1}{2}.\)

Замена: \(t=\displaystyle \frac{1}{x}.\)

\(3t^{2}-4t+1=0;\)

\(t=1\) или \(t=\displaystyle \frac{1}{3}.\)

\(x=1,\) то \(k=-3, \; a=\displaystyle \frac{1}{3}\) или \(x=3>\displaystyle \frac{3}{2}\) - не подходит.

Ответ: \(\displaystyle \frac{1}{3}.\)