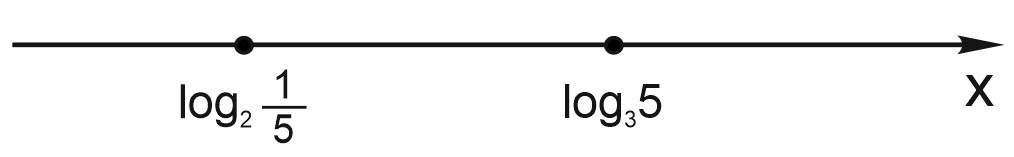Задание 13. Решение

а) Решите уравнение: \(log_{3}(x^{2}-2x)=1.\)

б) Найдите все корни этого уравнения, принадлежащие отрезку \([log_{2}0,2; log_{3}5].\)

Решение:

а) Представим \(1= log_{3}3.\)

Функция \(y= log_{3}t\) монотонно возрастает, поэтому если \(log_{3}t_{1}=log_{3}t_{2},\) то \(t_{1}=t_{2}\) при \(t_{1} > 0, \; t_{2} > 0.\)

Тогда уравнение равносильно системе:

\(log_{3}(x^{2}-2x)=1\Leftrightarrow \left\{\begin{matrix} x^{2}-2x> 0, \\x^{2}-2x=3; \end{matrix}\right.\Leftrightarrow x^{2}-2x-3=0\Leftrightarrow \left[\begin{matrix} x=3, \\x=-1. \end{matrix}\right.\)

б) \(x\in \Big[log_{2}\displaystyle \frac{1}{5};log_{3}5\Big].\)

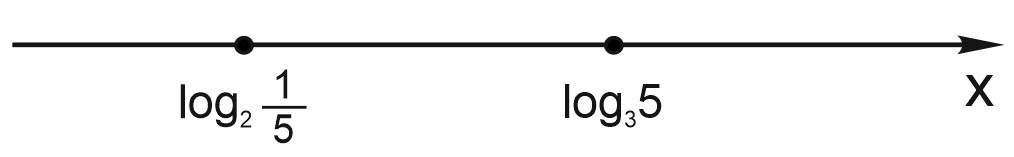
1) Сравним \(3\vee log_{3}5.\)

\(log_{3}27> log_{3}5,\) так как \(27 > 5,\) функция \(y= log_{3}t\) монотонно возрастает \(\Rightarrow 3> log_{3}5.\) Не подходит.

2) Сравним \(-1\vee log_{3}5.\)

\(-1< 0< log_{3}5.\)

Сравним \(-1\vee log_{2}\displaystyle \frac{1}{5}.\)

\(log_{2}\displaystyle \frac{1}{2}> log_{2}\displaystyle \frac{1}{5},\) так как \(\displaystyle \frac{1}{2}> \displaystyle \frac{1}{5},\) функция \(y= log_{2}t\) монотонно возрастает \(\Rightarrow log_{2}\displaystyle \frac{1}{5} < -1< log_{3}5,\) подходит.

Ответ: а) -1; 3; б) -1.