Задание 14. Решение

Дан прямоугольный параллелепипед \(ABCDA_{1}B_{1}C_{1}D_{1}.\) Точка \(O\) - центр грани \(A_{1}B_{1}C_{1}D_{1}.\) Сечение параллелепипеда плоскостями \((AOB)\) и \((BOC)\) являются прямоугольниками, \(AB\) и \(BC\) - их меньшие стороны соответственно. Известно, что \(AB\) и \(BC\) в 2 раза меньше соответственных больших сторон прямоугольников.

а) Докажите, что \(ABCD\) - квадрат.

б) Найдите угол между прямой \(A_{1}C\) и плоскостью \((BOC).\)

Решение:

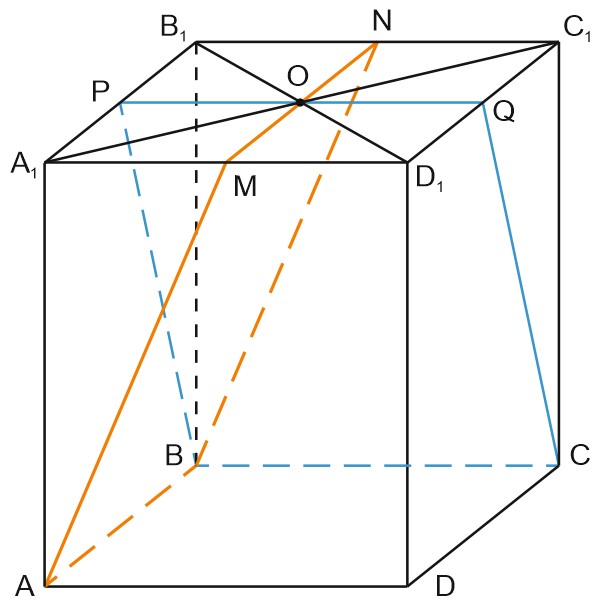
\((AOB)\cap (A_{1}B_{1}C_{1})=MN.\)

\(MN\parallel AB \; \) - как линии пересечения параллельных плоскостей третьей плоскость.

\(AM\in (AA_{1}D),\)

\((AA_{1}D)\perp AB\Rightarrow AM\perp AB, \; AMNB\) - прямоугольник.

Аналогично, \(PQ\parallel BC, \; O\in PQ, \; BPQC\) - прямоугольник.

\(AB=MN, \; BC=PQ.\)

По условию, \(AM=2AB, \; BP=2BC.\)

Пусть \(AB=a, \; BC=b, \; AA_{1}=c.\)

Из \(\triangle AA_{1}M\) по теореме Пифагора: \(AM^{2}=\Big(\displaystyle \frac{b}{2}\Big)^{2}+c^{2}.\)

Из \(\triangle BB_{1}Q\) по теореме Пифагора: \(BP^{2}=\Big(\displaystyle \frac{a}{2}\Big)^{2}+c^{2}.\)

По условию, \(AM=2a, \;BP=2b.\)

\(\left\{\begin{matrix}
4a^{2}=\displaystyle\frac{b^{2}}{4}+c^{2}, \\4b^{2}=\displaystyle\frac{a^{2}}{4}+c^{2}.
\end{matrix}\right.\)

Разность уравнений:

\(4(a^{2}-b^{2})=\displaystyle \frac{b^{2}-a^{2}}{4};\)

\(16(a^{2}-b^{2})=b^{2}-a^{2};\)

\(17(a^{2}-b^{2})=0;\)

\(a=b.\)

\(ABCD\) - квадрат.

Найдем угол между \(A_{1}C\) и \((BOC).\)

Если \(a=b,\) то \(c^{2}=a^{2}\cdot \Big(4-\displaystyle \frac{1}{4}\Big);\)

\(c^{2}=\displaystyle \frac{15}{4}a^{2}, \; c=\frac{a\sqrt{15}}{2}.\)

Введем систему координат, как показано на рисунке.

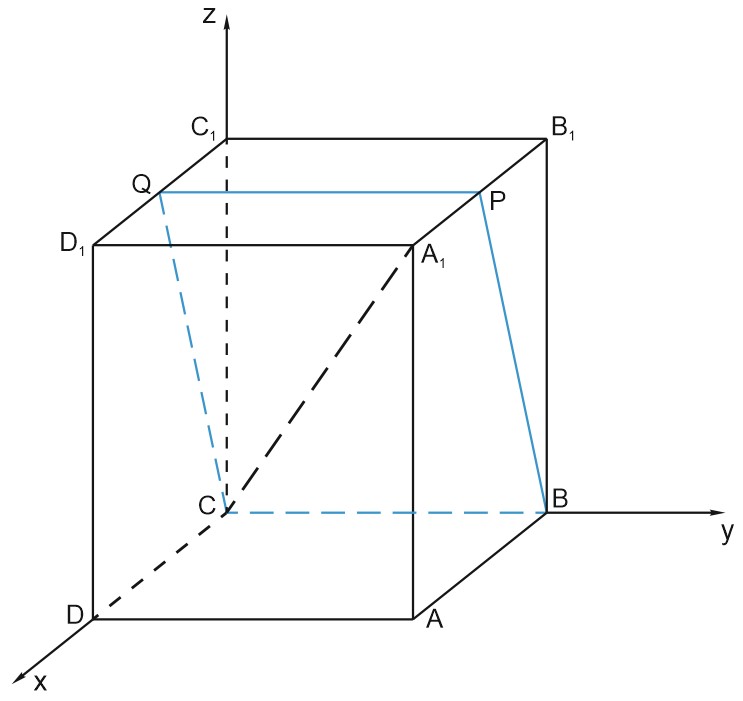
Пусть \(AB=BC=2,\) тогда \(AA_{1}=\sqrt{15}.\)

Запишем координаты точек: \(C(0; 0; 0), \; B(0; 2; 0), \; Q(1; 0; \sqrt{15}), \; A_{1}(2; 2; \sqrt{15}).\)

\(\vec{C}A_{1}=(2; 2; \sqrt{15}).\)

Запишем уравнение плоскости \((BQC)\) в виде \(Ax+By+Cz+D=0, \; O\in (BQC).\)

Точка \(C: \; D=0.\)

Точка \(B: \; 2B+D=0 \Rightarrow B=0.\)

Точка \(Q: \; A+\sqrt{15}C=0.\)

Пусть \(C=-1,\) тогда \(A=\sqrt{15}.\)

Нормаль к плоскости \((BQC): \; \vec{n}=(\sqrt{15};0;-1).\)

Угол между \(\vec{C}A_{1}\) и плоскостью \((BQC)\) найдем по формуле:

\(sin\varphi =\displaystyle \frac{\left | \vec{C}A_{1}\cdot \vec{n}\right |}{\left | \vec{C}A_{1}\right |\cdot \left | \vec{n}\right |}=\displaystyle \frac{2\sqrt{15}-\sqrt{15}}{\sqrt{4+4+15}\cdot \sqrt{15+1}}=\frac{\sqrt{15}}{4\sqrt{23}};\)

\(\varphi =arcsin\displaystyle \frac{\sqrt{15}}{4\sqrt{23}}.\)

Ответ: \(arcsin\displaystyle \frac{\sqrt{15}}{4\sqrt{23}}.\)