Задание 16. Решение

Зависимость количества \(Q\) в шт. при условии \(0\leq Q\leq 15000\) купленного у фирмы товара от цены \(P\) в руб. за шт. выражается формулой \(Q=15000-P\). Затраты на производство \(Q\) единиц товара составляют \(3000Q+1000000\) рублей. Кроме затрат на производство, фирма должна платить налог \(t\) рублей при условии \(0< t < 10000\) с каждой произведенной единицы товара. Таким образом, прибыль фирмы составляет \(PQ-3000Q-1000000-tQ\) рублей, а общая сумма налогов, собранных государством, равна \(tQ\) рублей.

Фирма производит такое количество товара, при котором ее прибыль максимальна. При каком значении \(t\) общая сумма налогов, собранных государством, будет максимальной?

Решение:

\(0\leq Q\leq 15 \cdot 10^{3}, \; Q\) - количество штук товара.

\(P\) - цена, \(Q=15 \cdot 10^{3}-P\Rightarrow P=15 \cdot 10^{3}-Q.\)

Затраты на производство \(Q\) единиц товара \(3 \cdot 10^{3}Q+10^{6}.\)

\(t\) - налог, \(0< t < 10^{4}.\)

Прибыль \(A=PQ-3 \cdot 10^{3}Q-10^{6}-tQ.\)

Общая сумма налогов \(B=tQ.\)

\(A=(15 \cdot 10^{3}-Q)\cdot Q-3 \cdot 10^{3}Q-tQ-10^{6}=-Q^{2}+Q\cdot (15 \cdot 10^{3}-3\cdot 10^{3}-t)-10^{6}=\)

\(=-Q^{2}+Q\cdot(12 \cdot 10^{3}-t)-10^{6}.\)

Построим эскиз графика функции \(A(Q).\) Это парабола, ветви вниз.

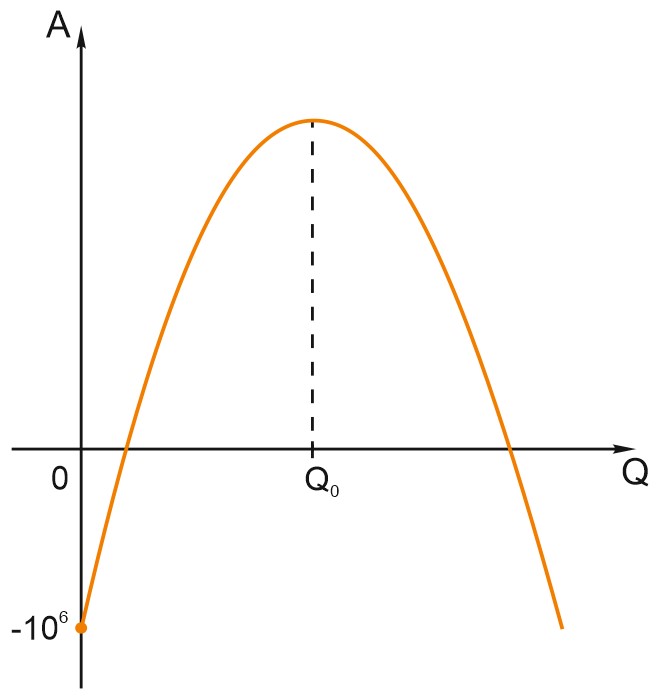
Прибыль максимальна при \(Q=Q_{0}\) - вершина параболы.

\(Q_{0}=\displaystyle \frac{12\cdot 10^{3}-t}{2};\)

\(Q_{0}=6\cdot 10^{3}-\displaystyle \frac{t}{2}.\)

Сумма налогов \(B=tQ_{0},\) так как прибыль максимальна.

\(B(t)=t\cdot \Big(6\cdot 10^{3}-\displaystyle \frac{t}{2}\Big)=-\displaystyle \frac{t^{2}}{2}+6\cdot 10^{3}t\) - парабола, ветви вниз, проходит через начало координат.

Построим эскиз графика функции \(B(t).\)

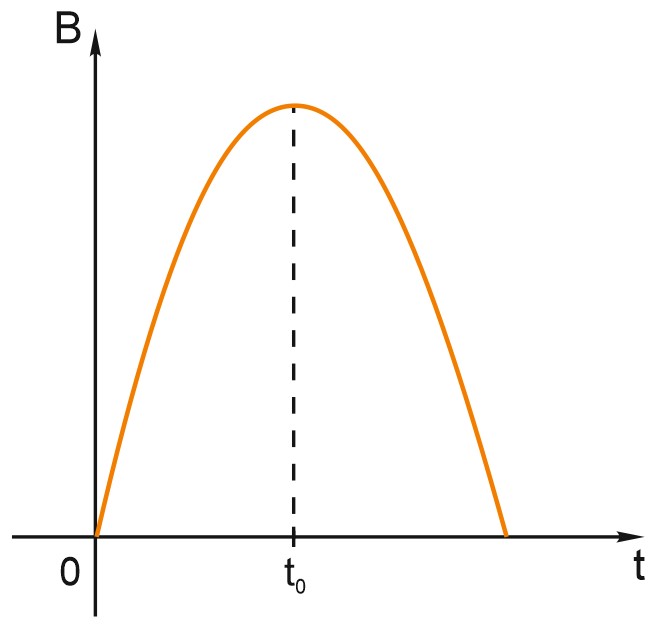
\(B(t)\) максимальна при \(t=t_{0}=6\cdot 10^{3}=6000.\)

По условию \(0< t < 10^{4}; \; 0< 6000 < 10^{4}\) - верно.

Ответ: 6000.