Задание 17. Решение

Дан ромб \(ABCD\). На диагонали \(AC\) отмечены точки \(M\) и \(N\) так, что \(AM=MN=NC.\) Прямая \(BM\) пересекает сторону \(AD\) в точке \(P\), а прямая \(BN\) пересекает сторону \(CD\) в точке \(Q\).

а) Докажите, что площадь четырехугольника \(BPDQ\) равна площади треугольника \(ADC\).

б) Найдите \(BD\), если известно, что \(AC=2\sqrt{5}\) и около пятиугольника \(MNQDP\) можно описать окружность.

Решение:

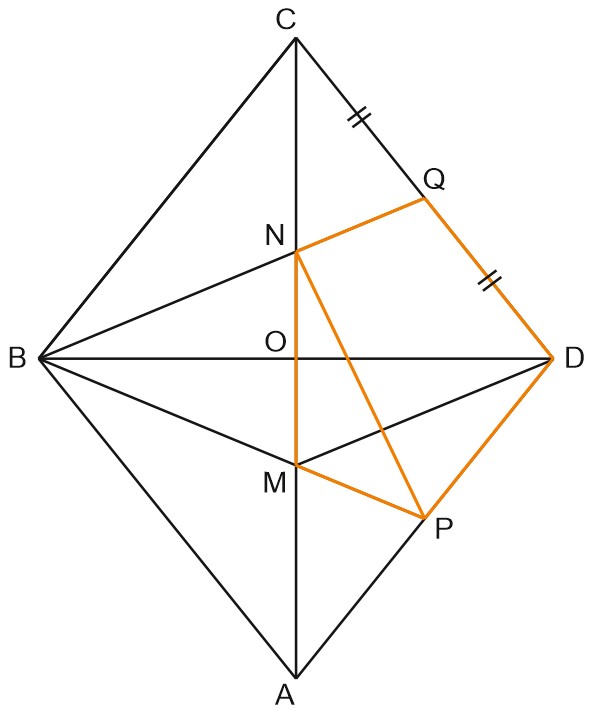
\(AM=MN=NC.\)

а) Докажем, что \(S_{BPDQ}=S_{\triangle ADC}.\)

\(CO\) - медиана \(\triangle BCD, \; CN : NO=2 : 1\Rightarrow N\) - точка пересечения медиан \(\triangle BCD,\) тогда \(BQ\) - медиана \(\triangle BCD.\)

\(CQ=DQ,\) также \(AP=PD.\)

\(S_{BPDQ}=S_{ABCD}-S_{\triangle BCQ}-S_{\triangle BAP}=\displaystyle \frac{1}{2}S_{ромба};\)

\(S_{BPDQ}=\displaystyle \frac{1}{2}S_{ромба}=S_{\triangle ADC}.\)

б) \(AC=2\sqrt{5}, \; BD\) - ?

MNQDP можно вписать в окружность \(\Rightarrow MNQP\) можно вписать в окружность.

\(\triangle NCQ\sim \triangle MCD\) по углу и двум сторонам,

\(\displaystyle \frac{CN}{CM}=\frac{CQ}{CD}=\frac{1}{2}\Rightarrow NQ\parallel MD;\)

\(MNQD\) - трапеция, вписанная в окружность, тогда \(MNQD\) - равнобедренная трапеция, \(MN=QD=\displaystyle \frac{1}{3}AC.\)

Пусть \(AC=3x,\) тогда \(MN=QD=x,\)

\(CD=2x, \; OC=\displaystyle \frac{3x}{2}.\)

Из \(\triangle COD\) по теореме Пифагора, \(OD=\sqrt{CD^{2}-OC^{2}}=\sqrt{4x^{2}-\displaystyle \frac{9x^{2}}{4}}=\sqrt{\displaystyle \frac{7x^{2}}{4}}=\displaystyle \frac{x\sqrt{7}}{2}.\)

\(BD=2OD=x\sqrt{7}=\displaystyle \frac{2\sqrt{5}\cdot \sqrt{7}}{3}=\frac{2\sqrt{35}}{3}.\)

Ответ: \(\displaystyle \frac{2\sqrt{35}}{3}.\)