Задание 18. Решение

Найдите все значения параметра \(a\), при каждом из которых система уравнений \(\left\{\begin{matrix}\displaystyle\frac{(y^{2}-7y-xy+4x+12)\sqrt{x+5}}{\sqrt{5-x}}=0, \\a=x+y\end{matrix}\right.\) имеет ровно два решения.

Решение:

\(\left\{\begin{matrix}\displaystyle\frac{(y^{2}-7y-xy+4x+12)\sqrt{x+5}}{\sqrt{5-x}}=0, \\a=x+y\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
\left[\begin{matrix}
y^{2}-7y-xy+4x+12=0, \\x+5=0,
\end{matrix}\right. \\x+5\geq 0,
\\5-x> 0,
\\y=x-a.
\end{matrix}\right.\)

Разложим левую часть I уравнения на на множители:

\( y^{2}-7y+12-xy+4x=(y-3)(y-4)-x(y-4)=(y-3-x)(y-4).\)

Система примет вид: \(\left\{\begin{matrix}
\left[\begin{matrix}
y-3-x=0, \\y-4=0,
\\x+5=0,
\end{matrix}\right. \\x+5\geq 0,
\\5-x> 0,
\\y=-x+a;
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
\left[\begin{matrix}
y=x+3, \\y=4,
\\x=-5,
\end{matrix}\right. \\-5\leq x< 5,
\\y=-x+a.
\end{matrix}\right.\)

Решим систему графически в координатах \( (x; y).\)

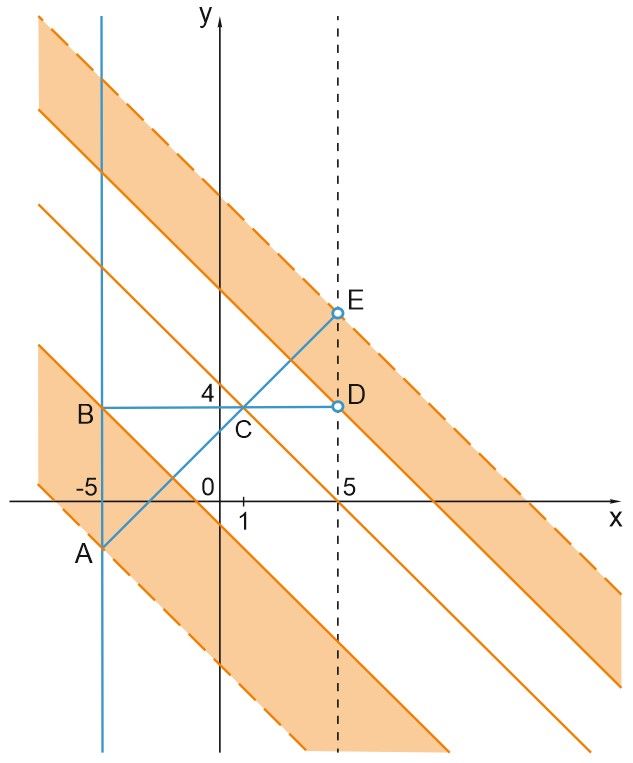
Графиком I уравнения исходной системы является совокупность прямых \(y=x+3, \; y=4\) и \(x=-5\) при условии \(-5\leq x< 5.\)

График уравнения \( y=-x+a \;\) - это прямая с угловым коэффициентом \(k=-1,\) сдвинутая на \(a\) единиц вверх или вниз.

Исходная система имеет ровно 2 решения, если прямая \(y=-x+a\) пересекает график первого уравнения ровно 2 раза. Это происходит, если прямая \(y=-x+a\) проходит выше точки \(A\) и не ниже точки \(B\), или через точку \(C\), или не ниже точки \(D\) и ниже точки \(E.\)

Для точки \(A: \; x=-5, \; y=x+3=-2, \; a=-7.\)

Для точки \(B: \; x=-5, \; y=4, \; a=-1.\)

Для точки \(C: \; y=4, \; y=x+3,\) тогда \(x=1, \; a=5.\)

Для точки \(D: \; x=5, \; y=4, \; a=9.\)

Для точки \(E: \; x=5, \; y=x+3=8, \; a=13.\)

Мы нашли значения \(a\), подставив \(x\) и \(y\) в формулу \(a=x+y.\)

Ответ: \(a\in (-7;-1]\cup \begin{Bmatrix}5\end{Bmatrix}\cup [9;13).\)