Центр подготовки к ЕГЭ > Материалы для подготовки к ЕГЭ и ОГЭ > Исследование графика функции

Исследование графика функции

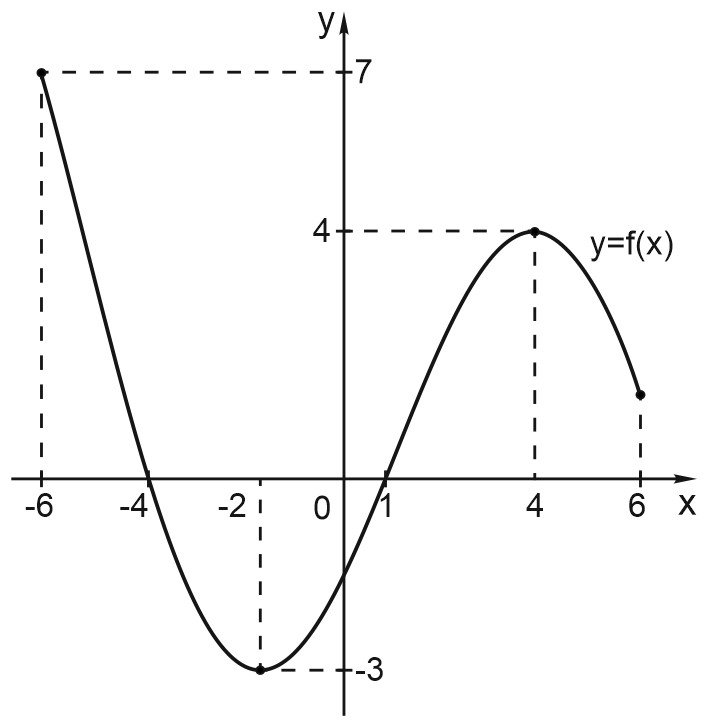
На рисунке изображен график функции $y=f\left( x \right)$ . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

область определения функции;
область значений функции;
нули функции;
промежутки возрастания и убывания;
точки максимума и минимума;
наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.

Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).

На нашем рисунке область определения функции $y=f\left( x \right)$ — это отрезок $\left[ -6; 6 \right]$ . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная $y$ . На нашем рисунке это отрезок $\left[ -3; 7 \right]$ — от самого нижнего до самого верхнего значения $y$ .

Нули функции — точки, где значение функции равно нулю, то есть $y=0$ . На нашем рисунке это точки $x=-4$ и $x=1$ .

Значения функции положительны там, где $y \textgreater 0$ . На нашем рисунке это промежутки $\left[ -6; -4 \right]$ и $\left[ 1; 6 \right]$ .
Значения функции отрицательны там, где $y \textless 0$ . У нас это промежуток (или интервал) от $-4$ до $1$ .

Важнейшие понятия — возрастание и убывание функции на некотором множестве $M$ . В качестве множества $M$ можно взять отрезок $\left[ a; b \right]$ , интервал $\left( a; b \right)$ , объединение промежутков или всю числовую прямую.

Функция $y=f\left( x \right)$ возрастает на множестве $M$ , если для любых $x_1$ и $x_2$ , принадлежащих множеству $M$ , из неравенства $x_2 \textgreater x_1$ следует неравенство $f\left( x_2 \right) \textgreater f\left( x_1 \right)$ .

Иными словами, чем больше $x$ , тем больше $y$ , то есть график идет вправо и вверх.

Функция $y=f\left( x \right)$ убывает на множестве $M$ , если для любых $x_1$ и $x_2$ , принадлежащих множеству $M$ , из неравенства $x_2 \textgreater x_1$ следует неравенство $f\left( x_2 \right) \textless f\left( x_1 \right)$ .

Для убывающей функции большему значению $x$ соответствует меньшее значение $y$ . График идет вправо и вниз.

На нашем рисунке функция $f\left( x \right)$ возрастает на промежутке $\left[ -2; 4 \right]$ и убывает на промежутках $\left[ -6; -2 \right]$ и $\left[ 4; 6 \right]$ .

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке $x=4$ — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке $x= -2$ — точка минимума.

Точка $x= -6$ — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и $x=6$ на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это $x=4$ и $x= -2$ .

А что делать, если нужно найти, например, минимум функции $y=f\left ( x \right )$ на отрезке $\left[ -4; 0 \right]$ ? В данном случае ответ: $y= -3$ . Потому что минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен $4$ . Он достигается в точке $x=4$ .

Можно сказать, что экстремумы функции равны $4$ и $-3$ .

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке $\left[ -6; 6 \right]$ равно $-3$ и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно $7$ . Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.

Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 08.01.2023

Исследование графика функции

Это полезно