Квадрат и его свойства

Квадрат – это прямоугольник, у которого все стороны равны.

Можно дать и другое определение квадрата.

Квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

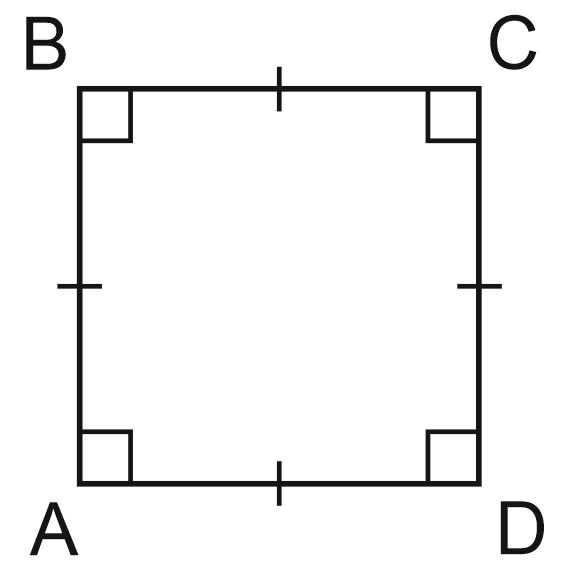
\(1.\) Все углы квадрата — прямые, все стороны квадрата — равны.

\(AB=BC=CD=AD;\)

\(\angle A= \angle B=\angle C=\angle D=90^{\circ }.\)

\(2.\) Диагонали квадрата равны и пересекаются под прямым углом.

\(AC=BD, AC \perp BD.\)

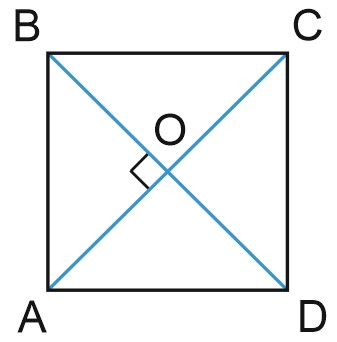
\(3.\) Диагонали квадрата делятся точкой пересечения пополам.

\(AO=OC, \; BO=OD.\)

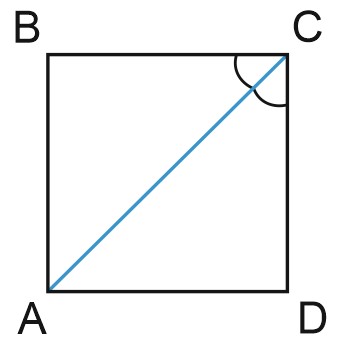
\(4.\) Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).

\(\angle BAC=\angle DAC, \; \angle ABD=\angle CBD, \; \angle BCA=\angle DCA, \; \angle CDB=\angle ADB.\)

\(5.\) Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника.

\(\triangle AOB=\triangle BOC=\triangle COD=DOA.\)

Периметр квадрата \(P\) в 4 раза больше его стороны и равен: \(P=4a.\)

Площадь квадрата равна квадрату его стороны: \(S=a^2.\)

Теорема 1. Диагональ квадрата равна произведению его стороны на \(\sqrt{2}\), то есть \(d=\sqrt{2} \cdot a.\)

Доказательство:

Рассмотрим квадрат \(ABCD.\) Проведем диагональ квадрата \(AC.\)

Треугольник \(ABC\) – прямоугольный с гипотенузой \(AC\). Запишем для треугольника \(ABC\) теорему Пифагора:

\(AC^{2}=AB^{2}+BC^{2};\)

\(AC^{2}=a^{2}+a^{2}=2a^{2}, \; AC=a\sqrt{2},\) что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны: \(\displaystyle r=\frac{1}{2}\cdot a.\)

Доказательство:

Пусть окружность с центром в точке \(O\) и радиусом \(r\) вписана в квадрат \(ABCD\) и касается его сторон в точках \(P, \; M, \; N, \; K.\)

Тогда \(OP \perp AB, \; ON \perp CD,\) поскольку \(AB\) параллельно \(CD\). Через точку \(O\) можно провести только одну прямую, перпендикулярную \(AB\), поэтому точки \(P, \; O\) и \(N\) лежат на одной прямой. Значит, \(PN\) – диаметр окружности. Поскольку \(APND\) – прямоугольник, то \(PN = AD\), то есть

\(2r=a, \; r=\displaystyle \frac{a}{2}\), что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали: \(R=\displaystyle \frac{\sqrt{2}}{2}\cdot a.\)

Доказательство:

Диагонали квадрата \(AC\) и \(BD\) равны, пересекаются в точке \(O\) и делятся точкой пересечения пополам.

Поэтому \(OA=OB=OC=OD\), т.е. точки \(A, \; B, \; C\) и \(D\) лежат на одной окружности, радиус которой \(R = \displaystyle \frac{d}{2}(d=AC=BD)\). Это и есть описанная около квадрата \(ABCD\) окружность.

По теореме \(1:d=a\sqrt{2}.\)

Тогда \(R=a\displaystyle \frac{\sqrt{2}}{2}\), что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

\(P=4a=4\sqrt{2}R=8r.\)

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем задачи ОГЭ и ЕГЭ на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

1. Найдите сторону квадрата, диагональ которого равна \(\sqrt{8}\).
Решение:

Мы знаем, что \(d=\sqrt{2} \cdot a.\) Тогда \(a=\genfrac{}{}{}{0}{\displaystyle d}{\displaystyle \sqrt{2}}= 2.\)

Ответ: 2.

2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

\(\displaystyle d=\sqrt{2}\cdot a \Rightarrow a=\frac{d}{\sqrt{2}}\Rightarrow a=\frac{1}{\sqrt{2}}.\)

Тогда по формуле площади квадрата:

\(\displaystyle S=a^{2}=\left (\frac{1}{\sqrt{2}} \right )^{2}=\frac{1}{2}=0,5.\)

Второй способ решения:

Воспользуемся формулой для площади ромба:

\(\displaystyle S=\frac{1}{2}d_{1}d_{2}=\frac{1}{2}d^{2}=0,5.\)

Ответ: 0,5

3. Найдите радиус окружности, описанной около квадрата со стороной, равной \(\sqrt{8}\).

Решение:

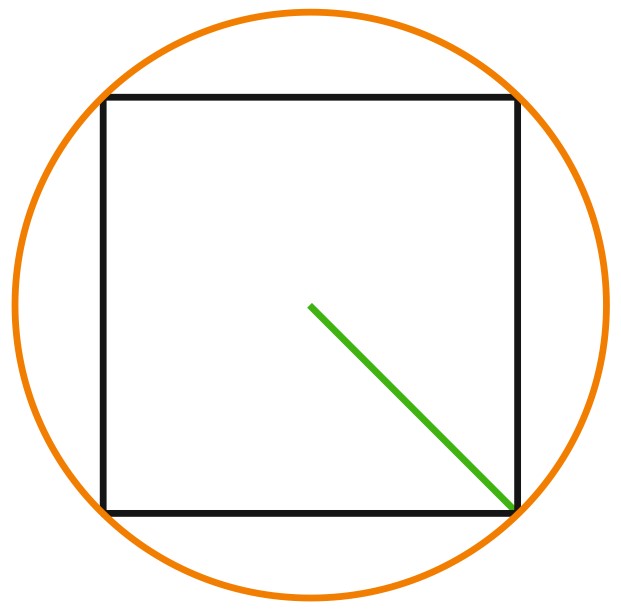
Радиус описанной окружности равен половине диагонали квадрата, поэтому

\(\displaystyle R=\frac{d}{2}=a\frac{\sqrt{2}}{2}=\sqrt{8}\cdot \frac{\sqrt{2}}{2}=2.\)

Ответ: 2.

4. Найдите сторону квадрата, описанного около окружности радиуса \(4\).

Решение:

Диаметр окружности равен стороне квадрата: \(a=2r=8.\)

Ответ: 8.

5. Радиус вписанной в квадрат окружности равен \(14\sqrt{2}\). Найдите диагональ этого квадрата.

Решение:

Сторона квадрата в два раза больше радиуса вписанной окружности:

\(a=2r=28\sqrt{2}.\)

Диагональ найдем, зная сторону квадрата:

\( d=a\sqrt{2}=28\sqrt{2}\cdot \sqrt{2}=56.\)

Ответ: 56.

6. Радиус вписанной в квадрат окружности равен \(11\sqrt{2}\). Найдите радиус окружности, описанной около этого квадрата.

Решение:

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

\(\displaystyle r=\frac{a}{2}; \; R=\frac{d}{2}; \; d=a\sqrt{2}.\)

Поэтому \(R=r\sqrt{2}=11\sqrt{2}\cdot \sqrt{2}=22.\)

Ответ: 22.

7. Найдите периметр квадрата, если его площадь равна 9.

Решение:

Найдем сторону квадрата: \(a=\sqrt{S}=\sqrt{9}=3.\)

Периметр квадрата со стороной 3 равен: \(P=4a=12.\)

Ответ: 12.

8. Найдите площадь квадрата, в который вписан круг площадью \(4\pi \).

Решение:

Площадь круга \(S_{kp}=\pi r^{2}=4\pi ,\) откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Ответ: 16.
9. Найдите радиус окружности, вписанной в квадрат \(ABCD\), считая стороны квадратных клеток равными \(\sqrt{2}\).

Решение:

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки.

Поскольку длина одной клеточки равна \(\sqrt{2}\), то сторона малого квадрата равна \(2\sqrt{2}\). А сторона квадрата \(ABCD\) равна \(2\sqrt{2}\cdot \sqrt{2}=4.\)

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Ответ: 2.
10. Найдите радиус \(r\) окружности, вписанной в четырехугольник \(ABCD\). В ответе укажите \(r \sqrt{10}\).

Решение:

Считаем стороны клеток равными единице. Четырехугольник \(ABCD\) – квадрат. Все его стороны равны, все углы – прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, \(AB\).

Она равна \(\sqrt{10}\). Тогда радиус вписанной окружности равен \(\genfrac{}{}{}{0}{\displaystyle \sqrt{10}}{\displaystyle 2}\). В ответ запишем \(r \sqrt{10}\).

Ответ: 5.