Ромб – это параллелограмм, все стороны которого равны.
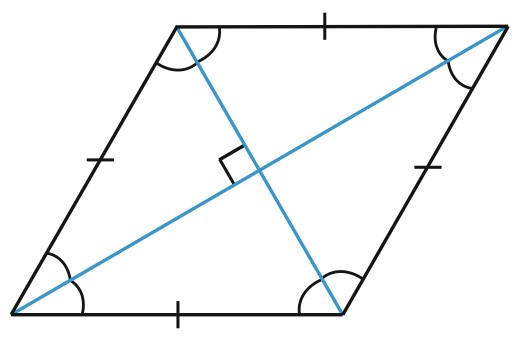
Свойства ромба:
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам.
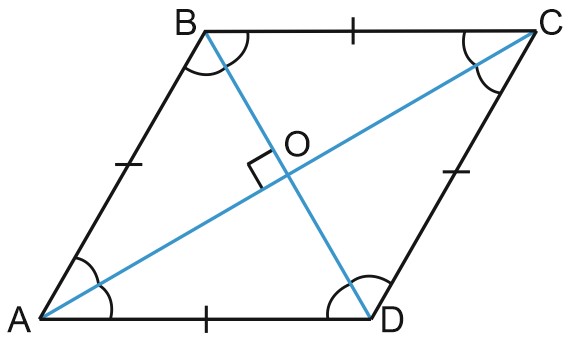
Это легко доказать. В самом деле, диагонали ромба делят его на 4 треугольника: \(AOB, \; BOC, \; COD, \; AOD,\) и все они равны по 3 сторонам.
Это значит, что углы \(AOB, \; BOC, \; COD, \; AOD\) равны, а сумма этих углов равна \(360\) градусов (полный круг).
Поэтому все эти углы – прямые, и треугольники \(AOB, \; BOC, \; COD, \; AOD\) прямоугольные.
А поскольку они равны друг другу, то \(\angle BAO=\angle DAO, \; \angle ABO=\angle CBO\). Диагонали ромба являются биссектрисами его углов.
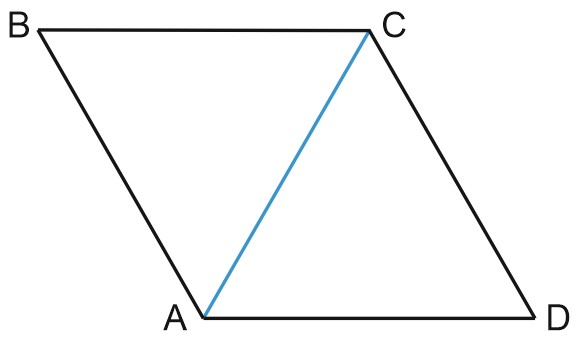
1. В ромбе \(ABCD\) угол \(ABC\) равен \(72^{\circ}\). Найдите угол \(ACD\). Ответ дайте в градусах.
Решение:
Углы \(ABC\) и \(BCD\) – односторонние при параллельных прямых \(AB\) и \(CD\) и секущей \(BC.\)
\(\angle BCD=180^{\circ}-72^{\circ}=108^{\circ}. \; CA\) – биссектриса этого угла.
Угол \(ACD\) равен половине угла \(BCD\), то есть \(108^{\circ} : 2 = 54^{\circ}.\)
Ответ: 54.
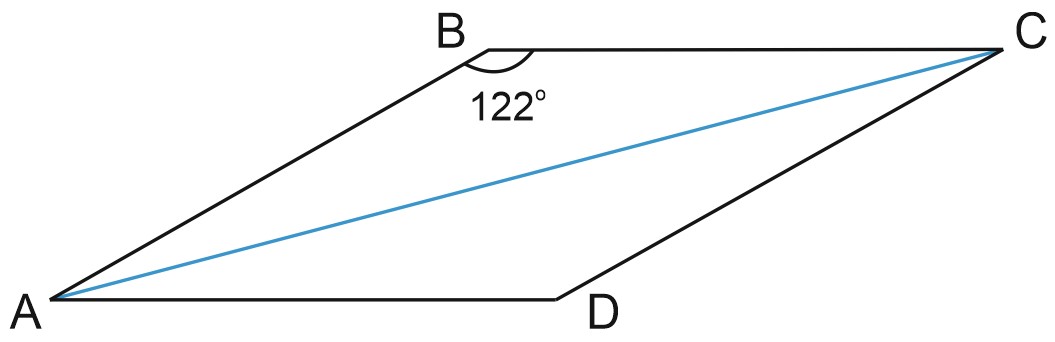
2. В ромбе \(ABCD\) угол \(ABC\) равен \(122^\circ.\) Найдите угол \(ACD\). Ответ дайте в градусах.
Решение:
\(\angle B\) и \(\angle C\) – это внутренние односторонние углы при параллельных прямых.
\(AB\parallel DC\) и секущей \(BC\), их сумма равна \(180^\circ .\)
Значит, \(\angle C=180^\circ -\angle B=180^\circ -122^\circ =58^\circ .\)
\(ABCD\) – ромб, диагонали ромба делят его углы пополам.
Тогда \(\angle ACD=58 : 2=29^\circ .\)
Ответ: 29.
3. Угол между стороной и диагональю ромба равен \(54^\circ .\) Найдите острый угол ромба.
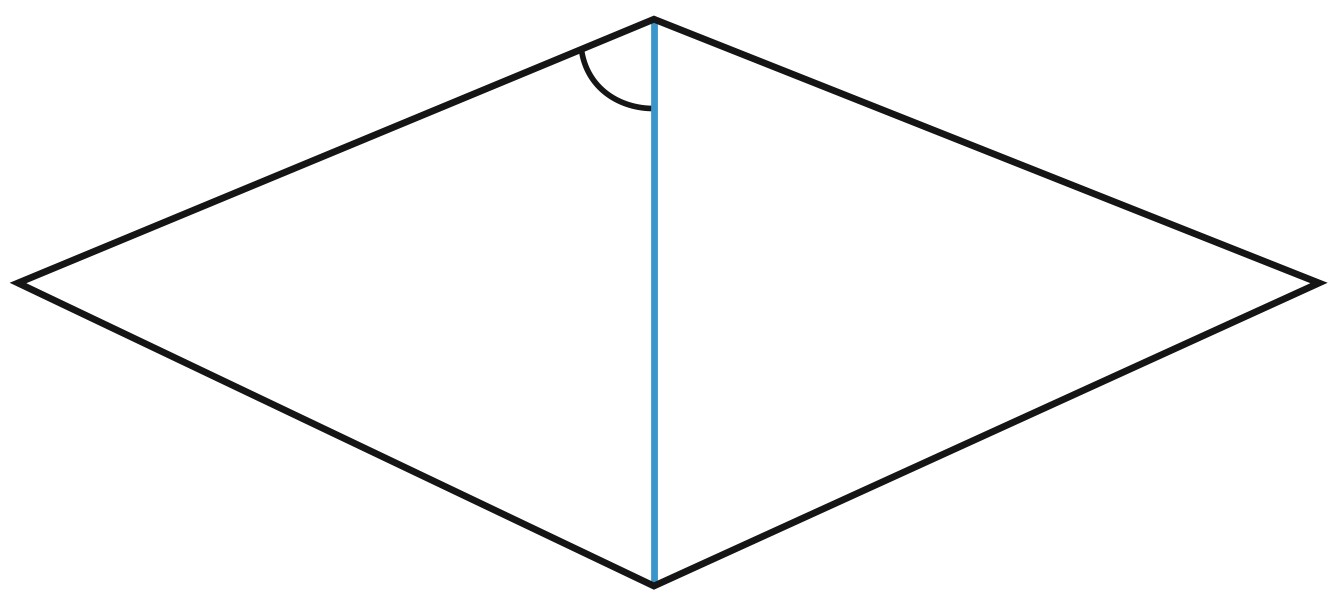
Решение:
Диагональ ромба делит его угол пополам, то есть является биссектрисой угла ромба.
Поэтому один из углов ромба равен \(54\cdot 2=108\) градусов, и это тупой угол ромба.
Тогда острый угол ромба равен \(180{}^\circ -108{}^\circ =72{}^\circ .\)
Ответ: 72.
4. Найдите высоту ромба, сторона которого равна \(\sqrt{3}\), а острый угол равен \(60^{\circ}\)?
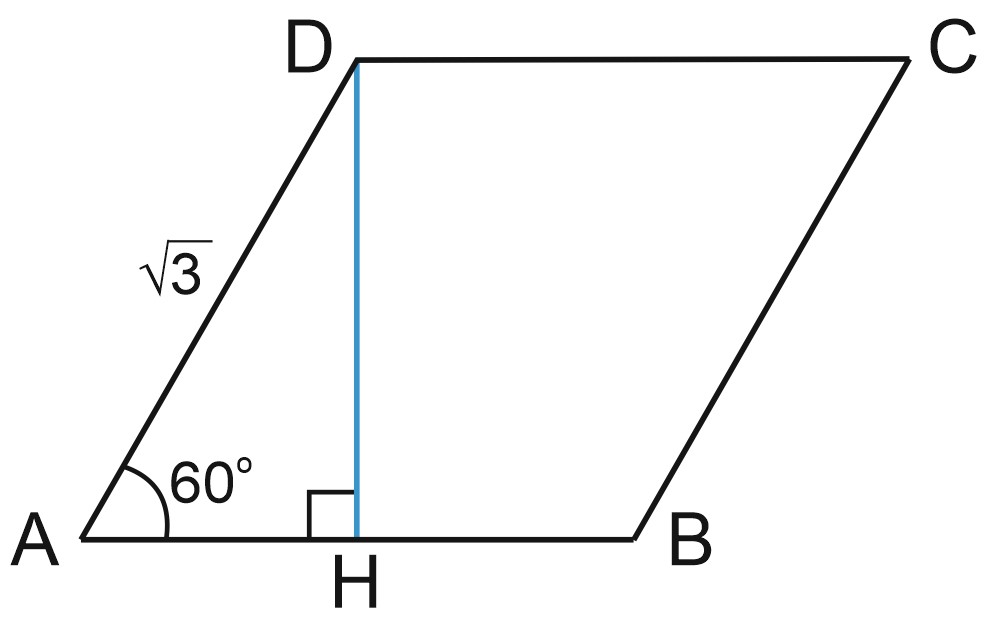
Решение:
Один из подходов к решению задач по геометрии — метод площадей. Он состоит в том, что площадь фигуры выражается двумя разными способами, а затем из полученного уравнения находится неизвестная величина.
Пусть \(a\) — сторона ромба.
Тогда \(S = a^2\cdot \sin 60^{\circ}= a\cdot h.\)
Отсюда \(h=a \sin 60^{\circ}=\displaystyle \frac{\sqrt{3}\cdot \sqrt{3}}{2}=1,5.\)
Ответ: 1,5.
5. Диагонали ромба относятся как \(3:4\). Периметр ромба равен \(200\). Найдите высоту ромба.
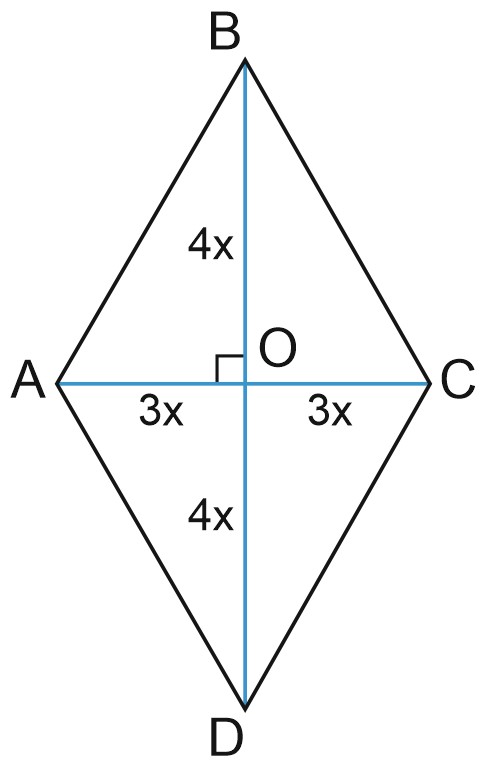
Решение:
Пусть диагонали ромба равны \(6x\) и \(8x.\)
Диагонали ромба перпендикулярны, значит, треугольник \(AOB\) — прямоугольный.
По теореме Пифагора \(AB^2 = AO^2 + OB^2;\)
\(AB^2 = 9x^2 + 16x^2;\)
\(AB^2 = 25x^2.\)
Отсюда \(AB=5x.\)
Поскольку периметр равен \(200,\)
\(5x \cdot 4=200,\)
\(x=10, \; AB=50\), а диагонали ромба равны \(60\) и \(80.\)
Нам надо найти высоту ромба.
Давайте запишем, чему равна площадь ромба. С одной стороны, \(S = a\cdot h\). С другой стороны, площадь ромба складывается из площадей двух равных треугольников \(ABC\) и \(ADC\), то есть равна \(60 \cdot 40 = 2400.\)
Отсюда \(h = S : a = 2400 : 50 = 48.\)
Ответ: \(48\).
В варианте ЕГЭ-2025 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
