Правильный треугольник

Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен \(60\) градусов.

Правильный треугольник называют еще равносторонним.

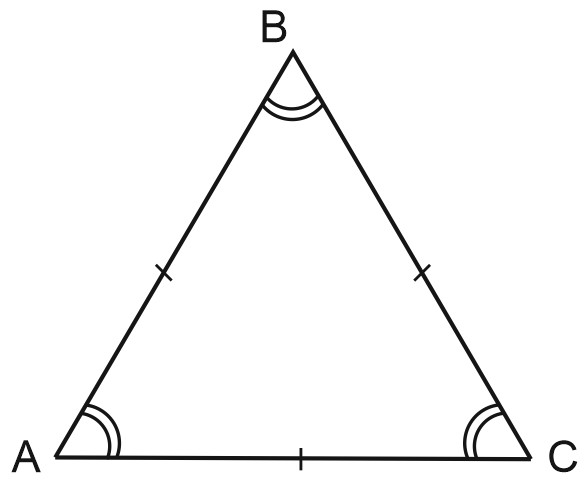
Каждая из высот правильного треугольника является также его медианой и биссектрисой.

Центры вписанной и описанной окружностей правильного треугольника совпадают.

Пусть сторона правильного треугольника равна \(a\).

Высота правильного треугольника: \(h=\genfrac{}{}{}{0}{\displaystyle \sqrt{3}}{\displaystyle 2} a.\)

Радиус окружности, вписанной в правильный треугольник: \(r=\genfrac{}{}{}{0}{\displaystyle \sqrt{3}}{\displaystyle 6} a.\)

Радиус описанной окружности в два раза больше: \(R=\genfrac{}{}{}{0}{\displaystyle \sqrt{3}}{\displaystyle 3} a.\)

Площадь правильного треугольника: \(S=\genfrac{}{}{}{0}{\displaystyle \sqrt{3}}{\displaystyle 4} a^2.\)

Докажем эти утверждения.

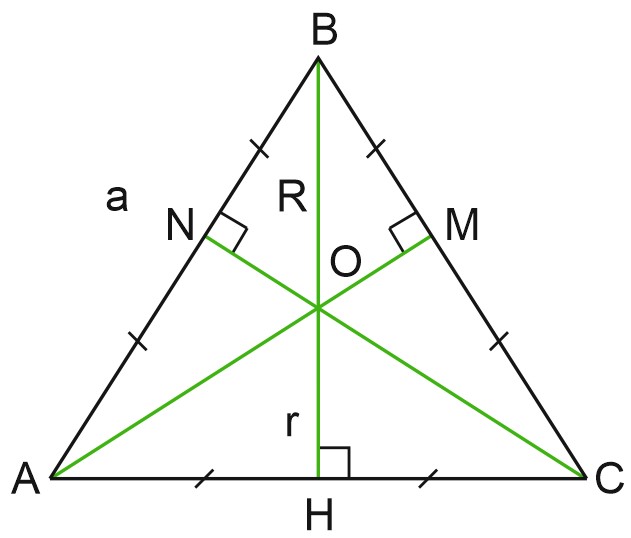
Формула радиуса окружности, вписанной в правильный треугольник \(r=\displaystyle \frac{a\sqrt{3}}{6}.\)

У равнобедренного треугольника медианы, биссектрисы, высоты и серединные перпендикуляры совпадают, и точка их пересечения является центром как вписанной, так и описанной окружностей.

1. Периметр правильного треугольника \(ABC\) равен \(15\). Найдите радиус вписанной и описанной окружностей.

Решение:

Длина стороны равностороннего треугольника \(ABC\)  равна \(15 : 3 = 5.\)

Радиусы \(r\) – вписанной и \(R\) – описанной окружностей можно найти по формулам:

\(\displaystyle r=\frac{a\sqrt{3}}{6}, R=\frac{a\sqrt{3}}{3},\) где \(a\) — сторона треугольника.

Значит, \(\displaystyle r=\frac{5\sqrt{3}}{6}, R=\frac{5\sqrt{3}}{3}.\)

Ответ: \(\displaystyle r=\frac{5\sqrt{3}}{6}, R=\frac{5\sqrt{3}}{3}.\)

Решая задачи по теме «Вписанные и описанные треугольники», мы часто пользуемся формулами площади треугольника, а также теоремой синусов.

Вот две полезные формулы для площади треугольника.

Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

\(S=p \cdot r\),

где \(p=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2} \left( a+b+c \right)\) — полупериметр,

\(r\) — радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части 2:

\(S=\genfrac{}{}{}{0}{abc}{4R},\)

где \(a, b, c\) — стороны треугольника, \(R\) — радиус описанной окружности.

2. Сторона правильного треугольника равна \(\sqrt{3}\). Найдите радиус окружности, вписанной в этот треугольник.

Задача решается в одну строчку. Радиус вписанной окружности \(r=\genfrac{}{}{}{0}{\displaystyle \sqrt{3}}{\displaystyle 6} a=0,5\).

3. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна \(6\).

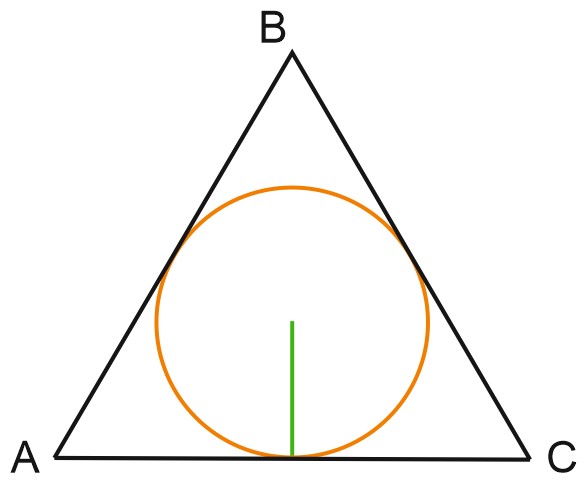
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен \(\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 3}\) высоты.

Ответ: \(2\).

4. Сторона правильного треугольника равна \(\sqrt{3}\). Найдите радиус окружности, описанной около этого треугольника.

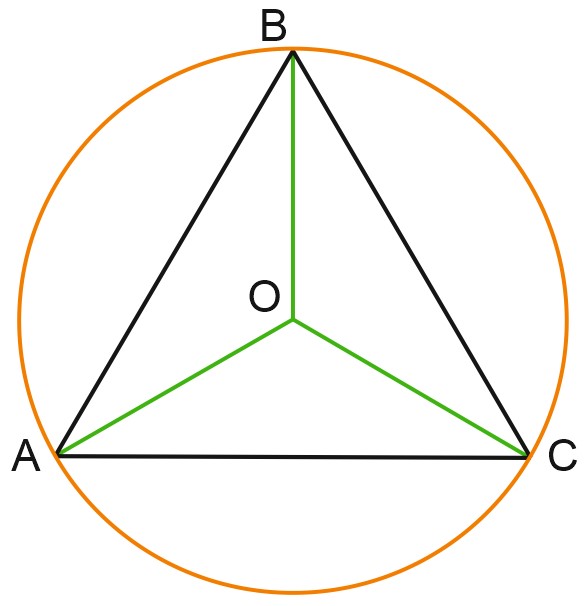
Радиус окружности, описанной вокруг правильного треугольника, равен \(\genfrac{}{}{}{0}{\displaystyle \sqrt{3}}{\displaystyle 3}a\).

Ответ: \(1\).