Углы при параллельных прямых и секущей

Пусть прямая \(c\) пересекает параллельные прямые \(a\) и \(b\). При этом образуется восемь углов, а сама прямая \(c\) называется секущей.

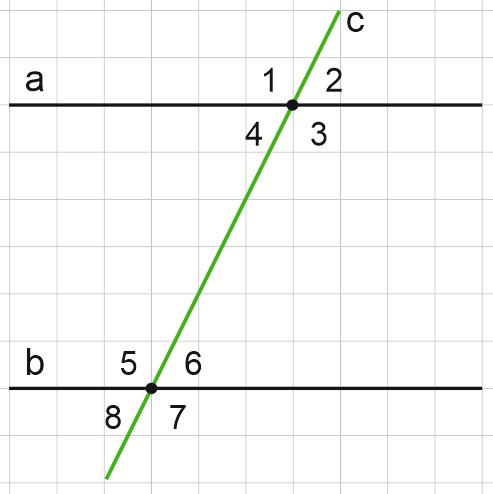
На этом чертеже легко найти пары смежных углов. Сумма смежных углов равна \(180\) градусов. Например, \(\angle 1+\angle 2=180^{\circ}; \; \angle 5+\angle 6=180^{\circ}.\)

Видим пары вертикальных углов. Напомним, что вертикальные углы равны:

\(\angle 1=\angle 3; \; \angle 5=\angle 7;\)

\(\angle 2=\angle 4; \; \angle 6=\angle 8.\)

А что же нового на чертеже?

Углы \(\angle 1\)  и \( \angle 5\) называются соответственными. Они одинаково расположены по отношению к параллельным прямым.

Соответственные углы равны. 

\(\angle 1=\angle 5.\)

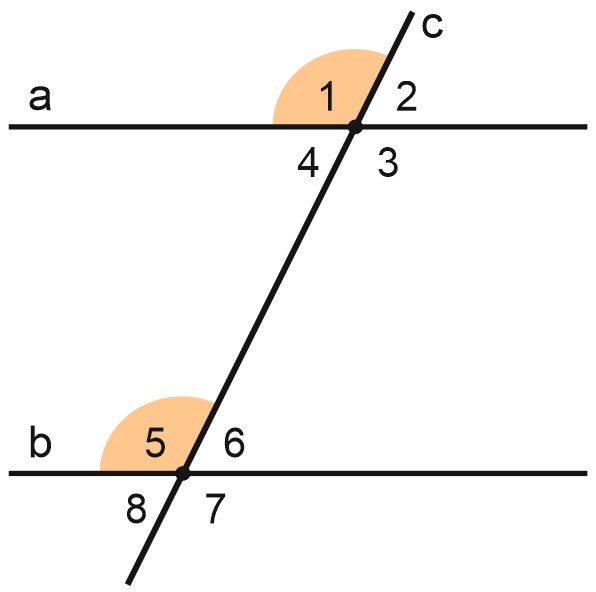
Аналогично, \(\angle 3=\angle 7.\)

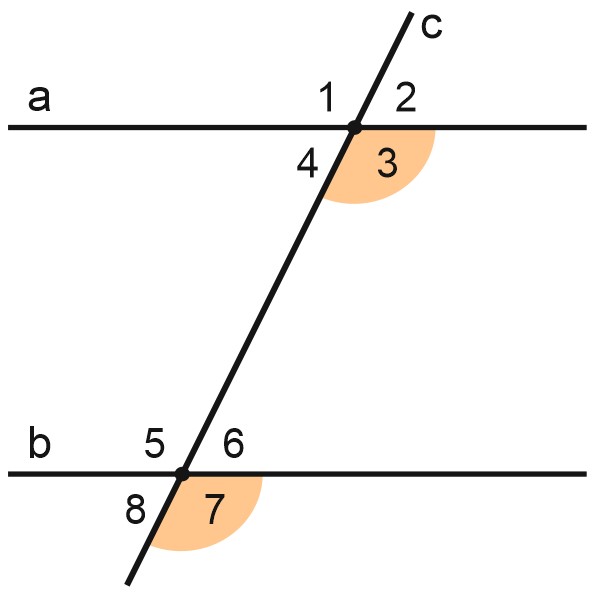
Также \(\angle 2=\angle 6, \; \angle 4=\angle 8.\)

Углы 4 и 6 – тоже равны между собой. При этом они лежат накрест друг от друга относительно секущей \(c\).

Такие углы называют накрест лежащими.

Накрест лежащие углы равны.

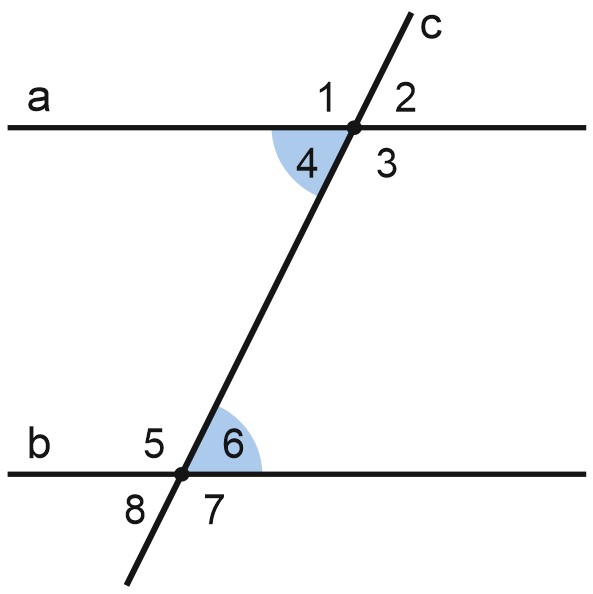
На рисунке углы 4 и 6 – внутренние накрест лежащие.

Вот еще одна пара накрест лежащих углов: \(\angle 3=\angle 5.\)

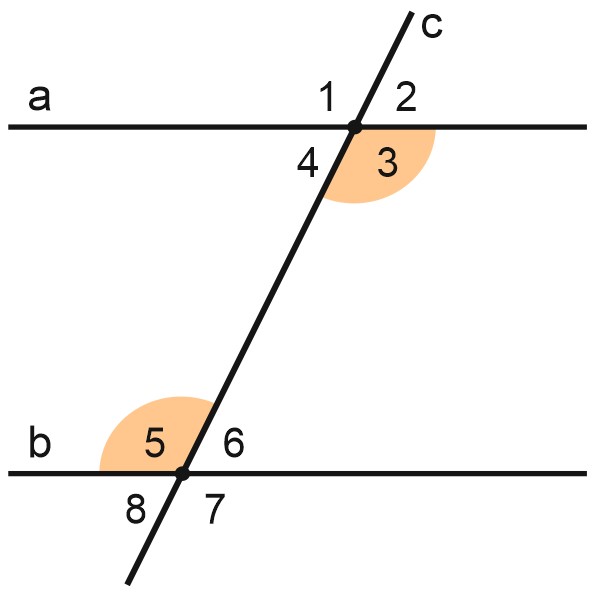
И еще здесь есть внешние накрест лежащие углы.

Например, \(\angle 2=\angle 8, \; \angle 1=\angle 7.\)

Посмотрим на углы 4 и 5: они в сумме дают \(180^{\circ}.\) При этом лежат они с одной стороны относительно секущей \(c\).

Такие углы называют односторонними.

Сумма односторонних углов равна \(180\) градусов.

\(\angle 4+\angle 5=180^{\circ} .\)

Углы 3 и 6 – тоже односторонние.

\(\angle 3+\angle 6=180^{\circ} .\)

Как это все применяется в задачах?

Например, нам даны две прямые, \(a\) и \(b\), а третья, прямая \(c\), их пересекает. И мы хотим выяснить, являются ли прямые \(a\) и \(b\) параллельными.

1) Если соответственные углы равны, то прямые параллельны.

\(\angle 1=\angle 5\Rightarrow a\parallel b.\) Аналогично, \(\angle 2=\angle 6\Rightarrow a\parallel b.\)

Можно взять любую пару соответственных углов, 3 и 7, 4 и 8.

2) Если накрест лежащие углы равны, то прямые параллельны.

\(\angle 3=\angle 5\Rightarrow a\parallel b;\)

\(\angle 2=\angle 8\Rightarrow a\parallel b.\)

Можно взять и другие пары накрест лежащих углов, 4 и 6 или 1 и 7.

3) Если сумма односторонних углов равна \(180\) градусов, то прямые параллельны.

\(\angle 4+\angle 5=180^{\circ} \Rightarrow a\parallel b;\)

\(\angle 3+\angle 6=180^{\circ} \Rightarrow a\parallel b.\)

Эти утверждения называются признаками параллельности прямых.

Признак – это то, что используется на практике для проверки.

В самом деле, как бы мы проверили, что две прямые параллельны? По определению, параллельные прямые – это те, которые нигде не пересекаются. Но мы же не будем идти по этим прямым до бесконечности, чтобы посмотреть пересекаются они или нет. А если выполняется признак параллельности, например, равны накрест лежащие углы, – значит, прямые параллельны.

1. На рисунке угол 1 равен \(123^{\circ}\). Найдите угол 6. Ответ выразите в градусах.

Решение:

Углы 1 и 2 – смежные, их сумма равна\(180\) градусов. Значит, угол 2 равен \(180^{\circ}-123^{\circ}=57^{\circ}.\)

Углы 2 и 6 равны как соответственные. Угол 6 равен \(57^{\circ}.\)

Ответ: 57.

2. На рисунке угол 6 равен \(43^{\circ}.\) Найдите угол 4. Ответ выразите в градусах.

Решение:

Углы 4 и 6 равны как внутренние накрест лежащие, значит, \(\angle 4 =43^{\circ}.\)

Ответ: 43.

3. Один из углов параллелограмма равен \(33^{\circ}\). Найдите больший угол этого параллелограмма. Ответ дайте в градусах.

Решение:

Вы помните из школьной программы, что параллелограмм – четырехугольник, имеющий две пары параллельных сторон.

\(33\) градуса – это острый угол. Острые углы в данном параллелограмме – это углы \(A\) и \(C\).

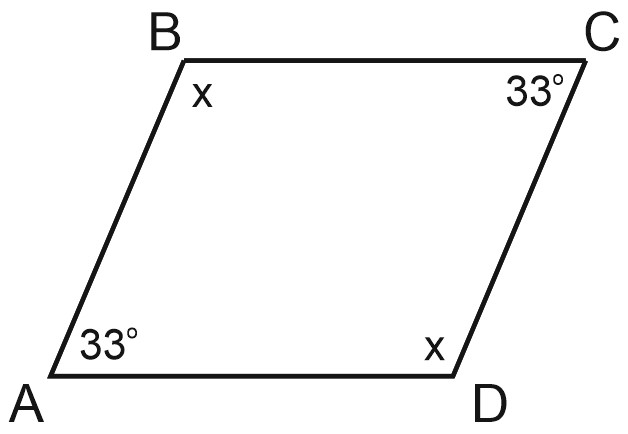
Мы хотим найти тупой угол параллелограмма, например, угол \(B\), который мы обозначили за \(x\). Углы \(A\) и \(B\) – это односторонние углы при \(AD\parallel BC\) и секущей \(AB\).

Составим уравнение:

\(x+33^{\circ}=180^{\circ};\)

\(x=147^{\circ}.\)

Ответ: 147.

4. Диагональ \(AC\) параллелограмма \(ABCD\) образует с его сторонами углы, равные \(40^{\circ}\) и \(35^{\circ}\). Найдите больший угол этого параллелограмма. Ответ дайте в градусах.

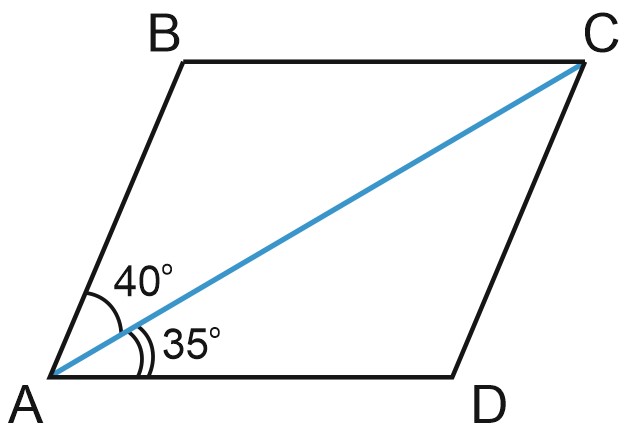
Решение:

\(\angle BAD=\angle BAC+ \angle CAD=40^{\circ}+35^{\circ}=75^{\circ}.\)

\(\angle BAD+ \angle ABC=180^{\circ}\) как односторонние углы при \(BC\parallel AD\) и секущей \(AB\).

\(75^{\circ}+\angle ABC=180^{\circ};\)

\(\angle ABC=105^{\circ}.\)

Ответ: 105.

5. Найдите острый угол параллелограмма \(ABCD\), если биссектриса угла \(A\) образует со стороной \(BC\) угол, равный \(41^{\circ}\). Ответ дайте в градусах.

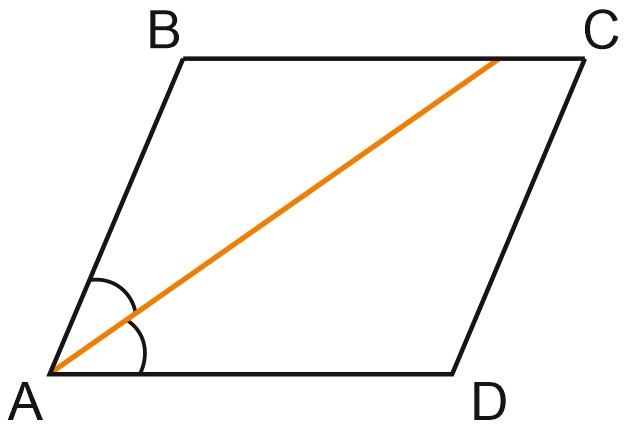
Решение:

Мы помним, что биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

На рисунке есть параллельные прямые. Поищем накрест лежащие и односторонние углы.

Углы \(BMA\) и \(MAD\) – накрест лежащие, и они равны \(41^{\circ}\).

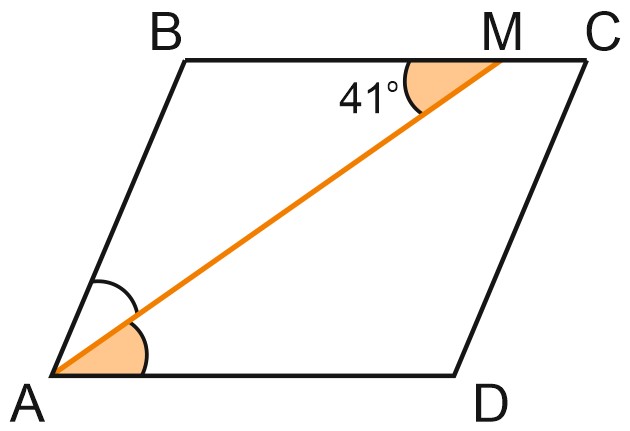
Углы \(BMA\) и \(MAD\) также равны, поскольку \(AM\) – биссектриса угла \(BAD\).

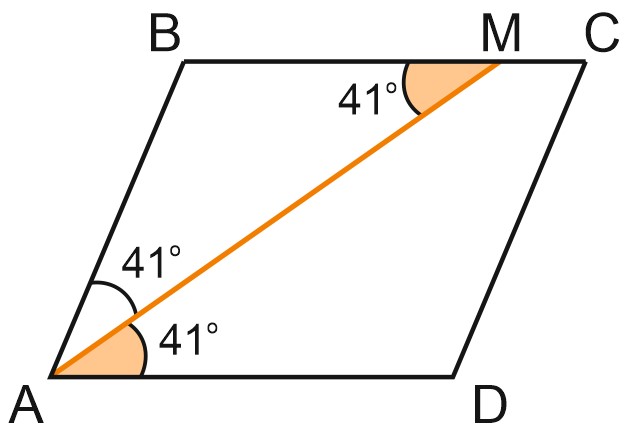
Острый угол параллелограмма равен: \(41^{\circ}+ 41^{\circ}=82^{\circ}\).

Ответ: 82.

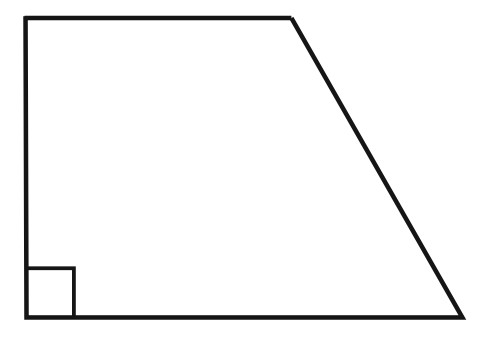
6. Один из углов прямоугольной трапеции равен \(82^{\circ}\). Найдите больший угол этой трапеции. Ответ дайте в градусах.

Решение:

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие - не параллельны.

82 градуса – это острый угол, он внизу справа. Подпишем его.

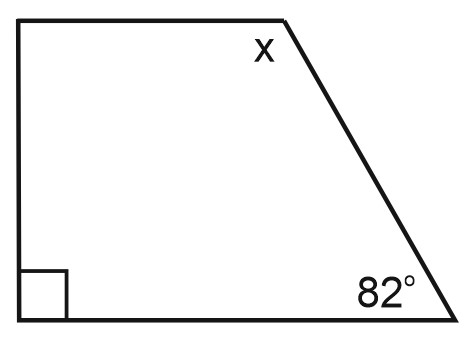
Углы \(x\) и \(82^{\circ}\) – односторонние при паралельных прямых. Их сумма равна \(180\) градусам.

Составим уравнение:

\(x+82^{\circ}=180^{\circ};\)

\(x=98^{\circ}.\)

Ответ: 98.

7. Биссектриса угла \(A\) параллелограмма \(ABCD\) пересекает сторону \(BC\) в точке \(K\). Найдите периметр параллелограмма, если \(BK=5, \; CK=14.\)

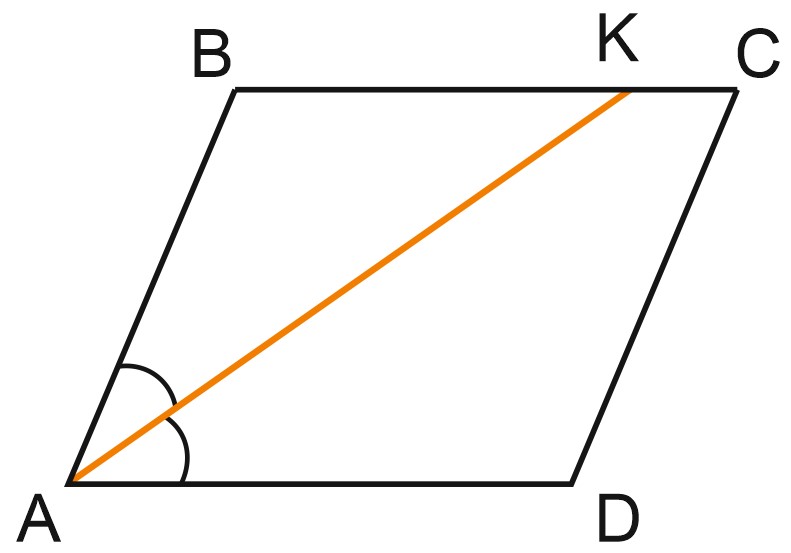
Решение:

\(BC\parallel AD, \; AK\) - секущая.

\(\angle KAD=\angle AKB\) как накрест лежащие.

\(BC=BK+KC=5+14=19,\)

\(\triangle ABK\) – равнобедренный.

Мы доказали важное утверждение.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

\(AB=BK=5.\)

\(P_{ABCD}=\left(AB+BC\right)\cdot 2;\)

\(P_{ABCD}=\left(5+19\right)\cdot 2=48.\)

Ответ: 48.

8. На плоскости даны четыре прямые. Известно, что \(\angle 1=120{}^\circ ,\) \(\angle 2=60{}^\circ ,\) \(\angle 3=55{}^\circ .\) Найдите \(\angle 4.\) Ответ дайте в градусах.

Решение:

\(\angle 1\) и \(\angle 2\) – внутренние односторонние углы,

\(\angle 1+\angle 2=120{}^\circ +60{}^\circ =180{}^\circ. \)

Отсюда следует, что \(a\parallel b.\)

Рассмотрим углы при параллельных прямых \(a\parallel b\) и секущей \(d\).

\(\angle 3\) и \(\angle 4\) – это односторонние углы, \(\angle 3=\angle 4=55{}^\circ. \)

Ответ: \(55.\)

9. Прямые \(m\) и \(n\) параллельны. Найдите \(\angle 3,\) если \(\angle 1=22{}^\circ ,\) \(\angle 2=72{}^\circ .\) Ответ дайте в градусах.

Решение:

\(m\parallel n\Rightarrow \angle 1=\angle 4=22{}^\circ \ \) как односторонние углы.

Сумма углов треугольника равна \(180{}^\circ .\)

Для треугольника на рисунке:

\(\angle 2+\angle 3+\angle 4=180{}^\circ \Rightarrow \angle 3=180{}^\circ -72{}^\circ -22{}^\circ =86{}^\circ .\)

Ответ: 86.

10. Прямые \(m\) и \(n\) параллельны (см. рисунок). Найдите \(\angle 3,\) если \(\angle 1=117{}^\circ , \; \angle 2=24{}^\circ .\) Ответ дайте в градусах.

Решение:

\(m\parallel n, \; \angle 2=\angle 4=24{}^\circ \) (как накрест лежащие углы).

\(\angle 1+\angle 4+\angle 3=180{}^\circ \) (развернутый угол).

Тогда \(\angle 3=180{}^\circ -\left(\angle 1+\angle 4\right)=180{}^\circ -\left(117{}^\circ +24{}^\circ \right)=39{}^\circ .\)

Ответ: 39.