Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла  угла треугольника. А что такое внешний угол треугольника?

Вспомним что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна \(180^{\circ}\).

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине \(B\) – это угол, смежный с углом \(\alpha\). Если угол \(\alpha\) острый, то смежный с ним угол – тупой, и наоборот.

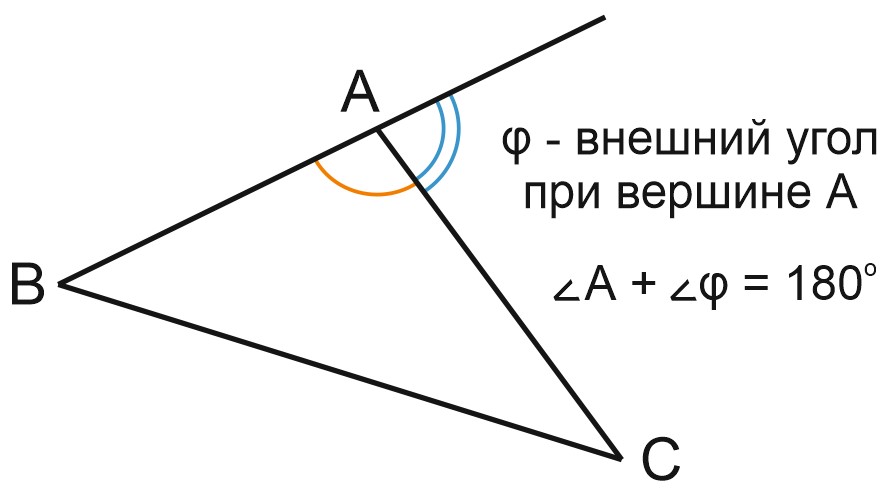
Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.

На нашем рисунке \(\varphi \) – внешний угол треугольника. Он является смежным с углом \(A\), поэтому \(\angle A+\varphi =180^{\circ}.\)

С другой стороны, сумма углов треугольника \(ABC\) равна \(180^{\circ}\).

\(\angle A+\angle B+\angle C=180^{\circ}.\)

Вычитая первое уравнение из второго, получим: \(\varphi =\angle B+\angle C\). Утверждение доказано.

1. В треугольнике \(ABC\) угол \(C\) равен \(133^{\circ}\). Найдите внешний угол при вершине \(C\). Ответ дайте в градусах.

Решение:

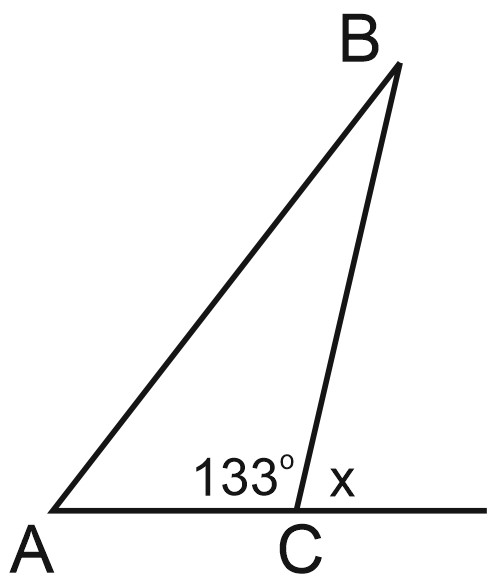
На чертеже мы видим два смежных угла, один из которых известен.

Составим уравнение:

\(x+133^{\circ}=180^{\circ};\)

\(x= 47^{\circ}.\)

Ответ: 47.

2. В треугольнике \(ABC\) внешний угол \(C\) равен \(87^{\circ}\), угол \(ABC\) равен \(47^{\circ}\). Найдите угол при вершине \(A\). Ответ дайте в градусах.

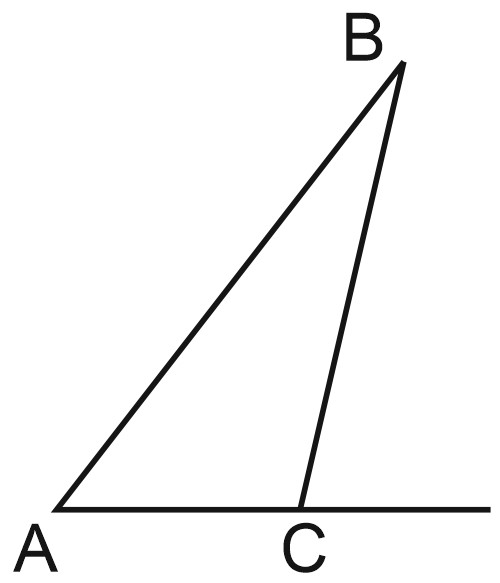
Решение:

Подпишем углы на рисунке.

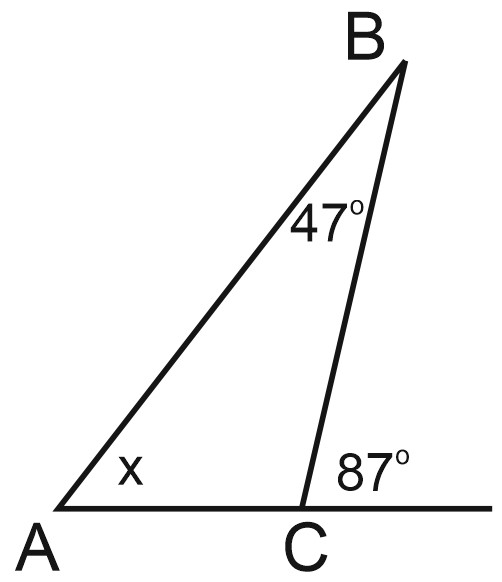
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Составим уравнение:

\(x+47^{\circ}=87^{\circ};\)

\(x= 40^{\circ}.\)

Ответ: 40.

3. Один из внешних углов треугольника равен \(85\) градусов. Углы, не смежные с данным внешним углом, относятся как \(2:3\). Найдите наибольший из них. Ответ дайте в градусах.

Решение:

Внешний угол треугольника равен сумме двух внутренних углом, не смежных с ним. Следовательно, сумма двух углов треугольника равна \(85\) градусов, а их отношение равно \(2:3\). Пусть эти углы будут \(2x\) и \(3x\).

Получим уравнение:

\(2x+3x=85\) и найдем \(x=17\).

Тогда \(3x=51\).

Ответ: 51.

Если угол \(\alpha  \) острый, то смежный с ним угол – тупой, и наоборот.

4. В треугольнике \(ABC\) проведена биссектриса \(AL\), угол \(ALC\) равен \({48}^\circ\), угол \(ABC\) равен \({41}^\circ\). Найдите угол \(ACB\). Ответ дайте в градусах.

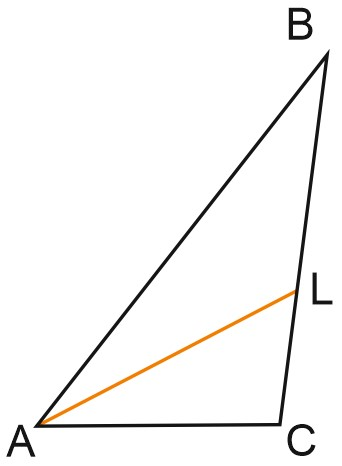
Решение:

\(\angle  ALC\) — внешний угол \(\triangle ABL,\) и он равен сумме двух внутренних углов, не смежных с ним. Значит, \(\angle BAL=\angle ALC-\angle ABL=48{}^\circ -41{}^\circ =7{}^\circ \).

\(AL\) — биссектриса \(\angle \ BAC\), а это значит, что \(\angle \ BAC=2\ \angle BAL=2\cdot 7{}^\circ =14{}^\circ \).

По теореме о сумме углов треугольника получаем:

\(\angle ACB=180{}^\circ -41{}^\circ -14{}^\circ =125{}^\circ .\)

Ответ: 125.

Пусть угол \(A\) равен \(\alpha   \). Тогда смежный с ним угол равен \({180}^\circ-\alpha  \). И мы можем найти синус, косинус и тангенс этого угла по формулам:

\(\sin \left( 180^{\circ} - \alpha \right) = \sin \alpha;\)

\(\cos \left( 180^{\circ} - \alpha \right) = - \cos \alpha;\)

\(tg \, \left( 180^{\circ} - \alpha \right) = - \, tg \, \alpha.\)

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
5. В треугольнике \(ABC\) угол \(C\) равен \(90^{\circ}\), \(\cos A = \genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle \sqrt{17}}\) . Найдите тангенс внешнего угла при вершине \(A\).

Решение:

Пусть \(\varphi\) — внешний угол при вершине \(A\).

\(\cos \varphi = - \cos A = - \genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle \sqrt{17}}.\)

Зная \(\cos \varphi\), найдем \(tg \, \varphi\) по формуле:

\(\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle \cos^2 \varphi}= 1 + tg^2 \, \varphi.\)

Получим: \(tg \, \varphi= - \genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 4} = - 0,25.\)

Ответ: -0,25.
6. В треугольнике \(ABC\) угол \(C\) равен \(90^{\circ}\), \(\cos A = 0,1\). Найдите синус внешнего угла при вершине \(B\).

Решение:

Задача решается за четыре секунды. Поскольку сумма углов \(A\) и \(B\) равна \(90^{\circ}, \; \sin B = \cos, \; A = 0,1\).

Тогда и синус внешнего угла при вершине \(B\) также равен \(0,1\).

Ответ: 0,1.