Высоты, медианы, биссектрисы треугольника
Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии.
1. Высота треугольника – это перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
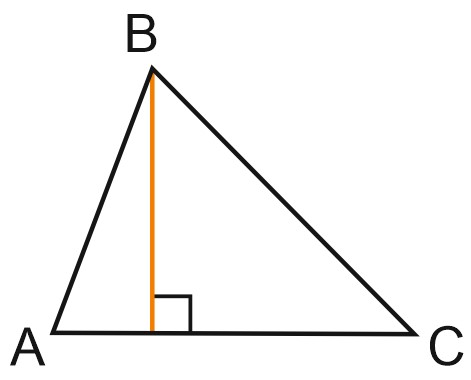
В тупоугольном треугольнике высота опускается на продолжение стороны.
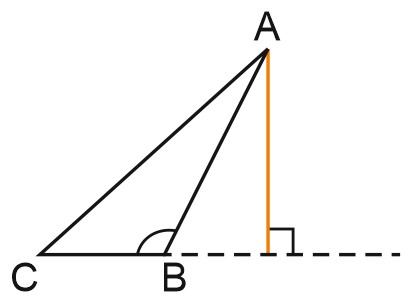
Три высоты треугольника всегда пересекаются в одной точке.
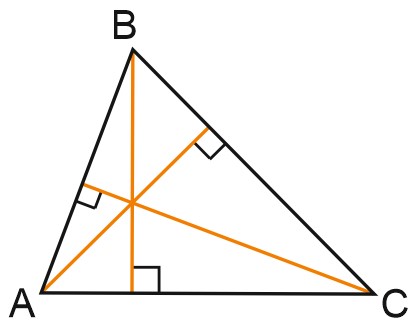
В случае тупого угла пересекаются продолжения высот.
Обо всех свойствах высот треугольника читать здесь.
2. Биссектриса треугольника – это луч, исходящий из вершины треугольника и делящий угол пополам.
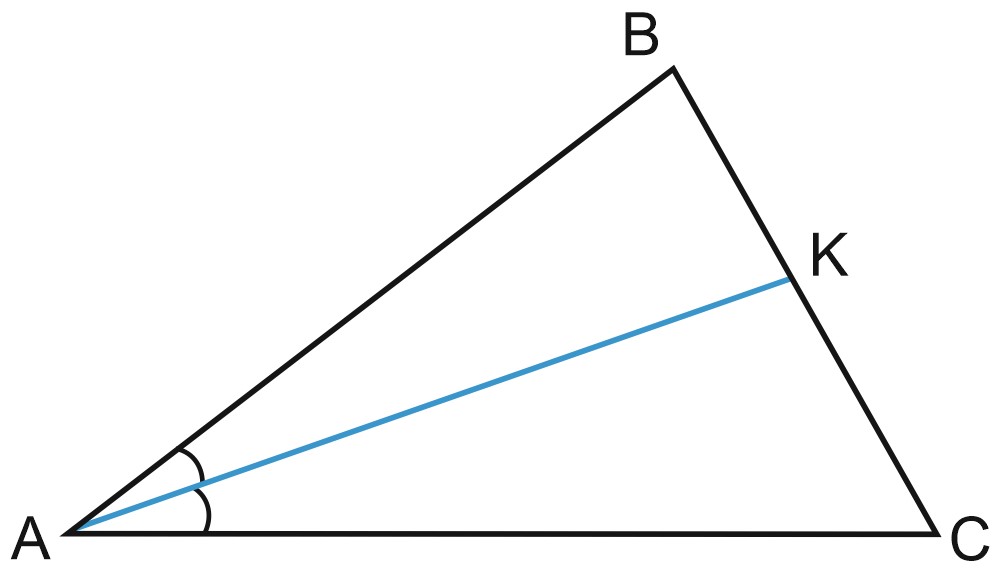
Все о биссектрисах треугольника здесь: Биссектриса треугольника.
3. Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
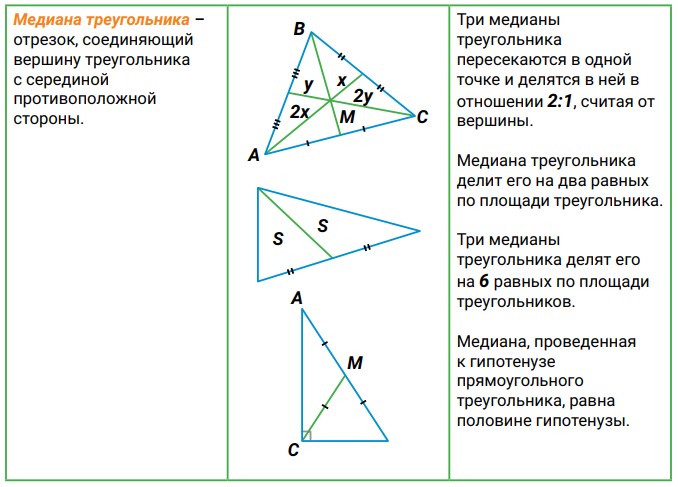
Читайте подробнее о свойствах медиан треугольника здесь.
Соберем в одну таблицу свойства высот, биссектрис, медиан треугольника:
Высоты, биссектрисы, медианы треугольника
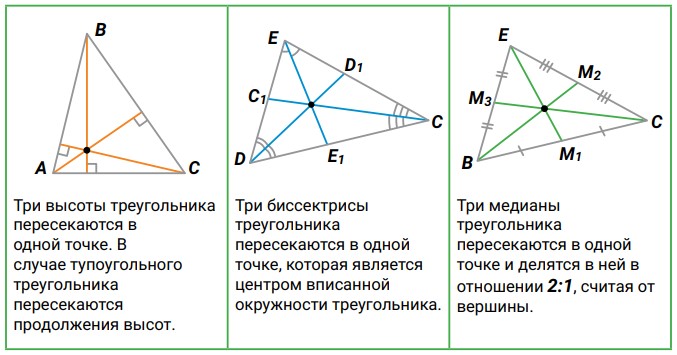
Задачи ОГЭ м ЕГЭ по теме «Высоты, биссектрисы, медианы треугольника»
1. Острые углы прямоугольного треугольника равны \(29^{\circ}\) и \(61^{\circ}\). Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
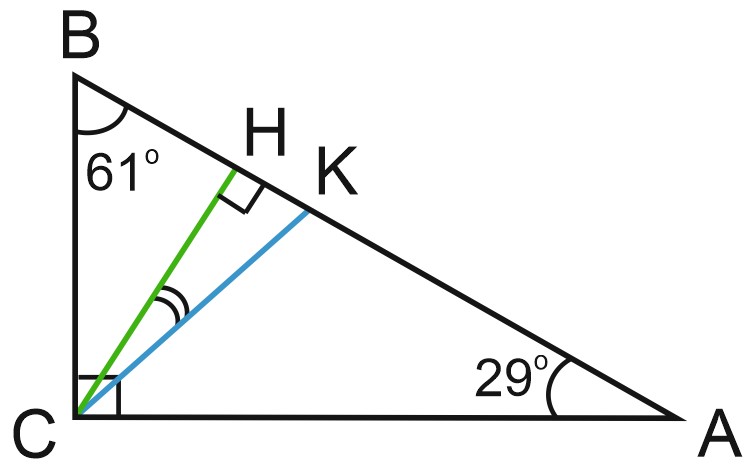
Пусть \(CH\) — высота, проведенная из вершины прямого угла \(C, \; CK\) — биссектриса угла \(C\).
Тогда \(\angle ACH = \angle ABC = 61^{\circ}\);
\(\angle ACK = 90^{\circ}:2=45^{\circ}\).
Угол между высотой и биссектрисой — это угол \(\angle KCH\).
\(\angle KCH = \angle ACH - \angle ACK = 61^{\circ}-45^{\circ}=16^{\circ}\).
Ответ: 16.
2. Острые углы прямоугольного треугольника равны \(24^{\circ}\) и \(66^{\circ}\). Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:

Рассмотрим треугольник \(ABC\), в котором угол \(C\) – прямой, \(CD\) – высота, \(CM\) – медиана.
\(\angle CAB=24^{\circ }, \; \angle ABC=66^{\circ }.\) Требуется найти угол \(MCD\).
Треугольник \(CMB\) – равнобедренный, т. к. медиана \(CM\) равна половине гипотенузы \(AB\).
Следовательно, \(\angle MCB=\angle MBC=66^{\circ }.\)
\(\angle BCD=\angle BAC=24^{\circ }.\)
Искомый \(\angle MCD=\angle MCB- \angle BCD=66^{\circ }-24^{\circ }=42^{\circ }.\)
Ответ: 42.
3. Острые углы прямоугольного треугольника равны \(23^{\circ}\) и\(67^{\circ}\). Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
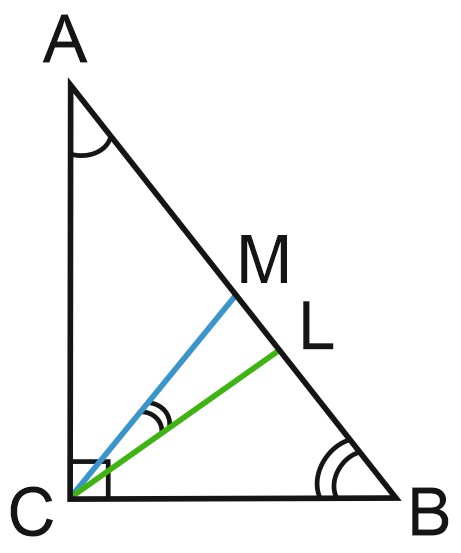
Рассмотрим треугольник \(ABC\), в котором угол \(C\) – прямой, \(CL\) – биссектриса, \(CM\) – медиана.
\(\angle CAB=23^{\circ }, \; \angle ABC=67^{\circ }\). Требуется найти угол \(MCL\).
Треугольник \(CMB\) – равнобедренный, т. к. медиана \(CM\) равна половине гипотенузы \(AB\).
Следовательно, \(\angle MCB=\angle MBC=67^{\circ }.\)
\(\angle BCL=\angle ACL=90^{\circ }:2=45^{\circ }\), т. к. \(CL\) – биссектриса.
Искомый \(\angle MCL=\angle MCB- \angle BCL=67^{\circ }-45^{\circ }=22^{\circ }.\)
Ответ: 22.
4. В треугольнике \(ABC\) \(CD\) – медиана, угол \(ABC\) равен \(90^{\circ }\), угол \(B\) равен \(58^{\circ }\). Найдите угол \(ACD\). Ответ дайте в градусах.

Решение:
В прямоугольном треугольнике медиана равна половине гипотенузы.
Поэтому \(AD=CD=BD.\)
Треугольник \(ADC\) равнобедренный, следовательно, углы при основании равны: \(\angle ACD=\angle CAD.\)
Поскольку в прямоугольном треугольнике сумма острых углов равна \(90\) градусов, получим:
\(\angle CAD=90^{\circ}-\angle ABC=90^{\circ}-58^{\circ}=32^{\circ};\)
\(\angle ACD=\angle CAD=32^{\circ}.\)
Ответ: 32.










































