Квадратичная функция. Парабола. Свойства и график

Мы знаем, что такое линейная функция. Конечно, функции бывают не только линейные. В этой теме мы изучаем квадратичную функцию. В ее формулу входит \(x\) в квадрате, ее график - парабола.

Мы помним, как выглядит парабола \(y = x^2\). В седьмом классе мы рисовали таблицу и строили график \(y = x^2\) по точкам.

Вот такая была таблица. Мы берем \(x\) из первой строчки, возводим его в квадрат и записываем во вторую строчку значение \(y\).

\(x\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(y\)	\(9\)	\(4\)	\(1\)	\(0\)	\(1\)	\(4\)	\(9\)

Наносим точки с координатами\( (x; y)\) на координатную плоскость. Это точки:

\((-3; 9), \; (-2; 4); \; (-1; 1); \; (0; 0); \; (1; 1); \; (2; 4); \; (3; 9).\)

И соединяем эти точки плавной кривой. Получается график, который называется параболой.

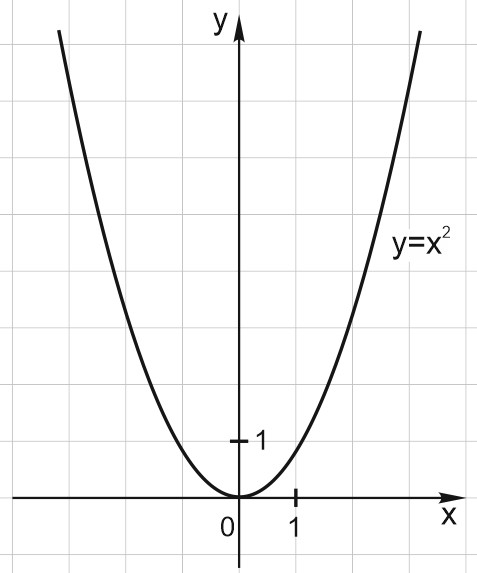
Посмотрим внимательно на этот график и перечислим его основные свойства.

1) Функция \(y = x^2\) определена для всех \(x\), от минус бесконечности до плюс бесконечности. Другими словами, в формулу \(y = x^2\) можно подставить любой \(x\).

2) Область значений этой функции – неотрицательные числа. Весь график расположен не ниже оси \(X\), потому что квадрат любого числа – величина неотрицательная.

3) Если \(x=0\), то \(y=0\). Можно сказать, что при \(x=0\) парабола касается оси \(X\).

4) Точка \((0; 0)\) на графике называется вершиной параболы. Конечно, это немного странно: ведь точка \((0; 0)\) на графике – это, наоборот, ямка, самая низкая точка. Но вот такое у нее название.

5) Легко заметить, что график квадратичной функции симметричен относительно оси \(Y\). Например, при \(x=3\) и \(x=-3\) функция принимает одинаковые значения, равные \(9\).

При \(x=2\) и \(x=-2\) также одинаковые значения, равные \(4\).

В общем виде формула квадратичной функции выглядит так:

\(y = ax^2 + bx + c.\)

Будем учиться строить график квадратичной функции, заданной такой формулой.

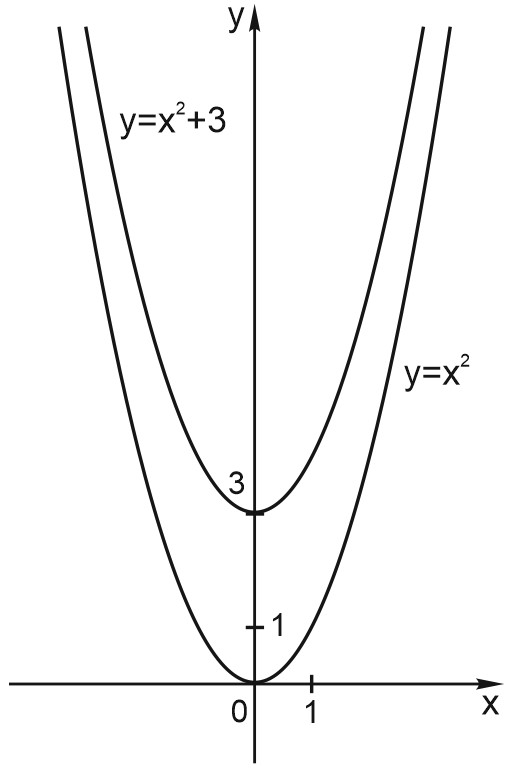
1. Начнем с простого случая. Построим график функции \(y = x^2 + 3\).

График функции \(y = x^2 + 3\)  сдвинут на \(1\) вверх по отношению к графику функции \(y = x^2\). Потому что к каждому значению функции \(y = x^2\) мы прибавили \(3\), и график сдвинулся на \(3\) вверх.

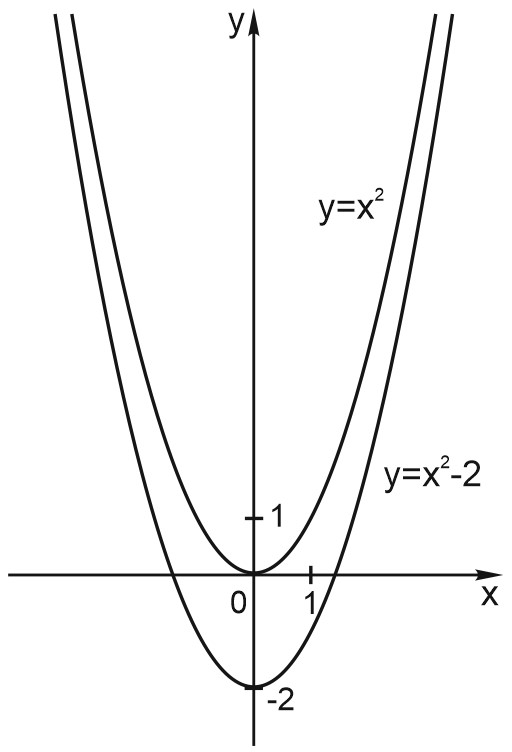
2. Следующий -  график функции \(y = x^2 - 2\) сдвинут на \(2\) вниз по отношению к графику функции \(y = x^2\).  Потому что из каждого значения функции \(y = x^2\) мы вычитаем \(2\), и график сдвигается на \(2\) вниз.

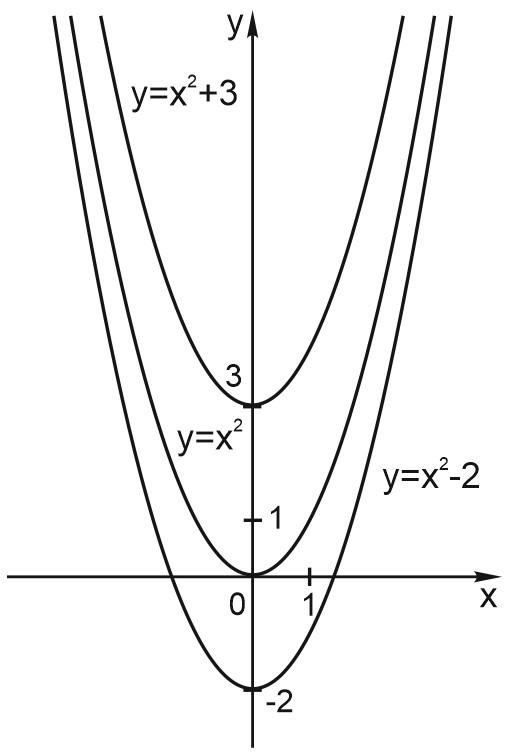
Мы поняли, как строить график функции \(y = x^2 + c\).

Если \(c>0\), то он будет сдвинут на \(c\) вверх по отношению к графику функции \(y = x^2\). Если \(c<0\), то сдвинут на \(c\) вниз.

Как будто мы вырезали шаблон графика \(y = x^2\) из бумаги и двигаем его вверх-вниз.

Можно сказать, что график функции \(y = x^2 + c\) получается из графика \(y = x^2\) параллельным переносом вверх (если \(c>0\)) или вниз (если \(c<0\)).

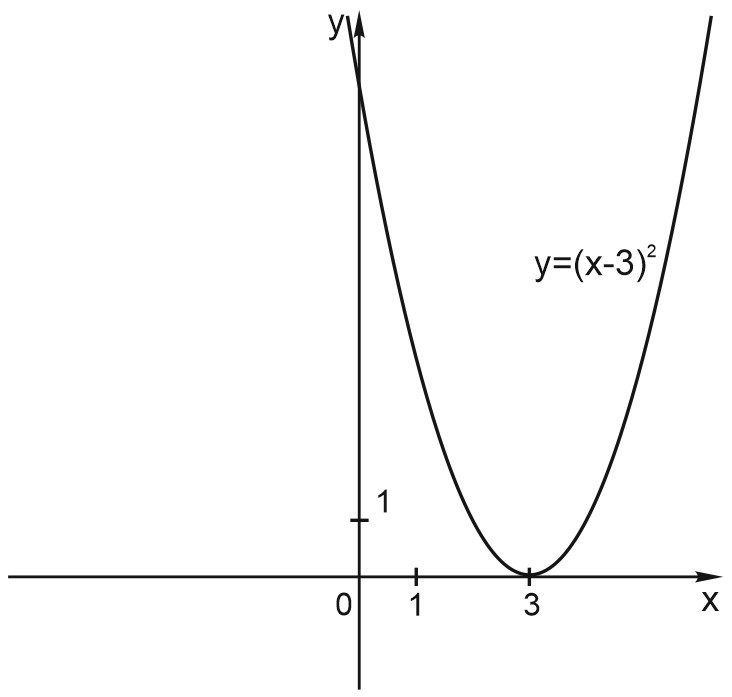
3. Построим график функции \(y = (x-3)^2\).

Тоже параллельный перенос. Но как же теперь надо подвинуть наш шаблон? На самом деле достаточно понять, куда движется вершина параболы. Куда вершина – туда поедет и вся парабола.

У параболы \(y = x^2\) вершина (то есть самая низкая точка на графике) - это \((0; 0)\).

И это понятно. Ведь \(x^2\geq 0\) при всех \(x\).

Выражение \((x-3)^2\) тоже не может быть меньше нуля. А значение, равное нулю, оно принимает, если \(x=3\). Точка \((3; 0)\) будет вершиной параболы \(y = (x-3)^2\).

Получается, что график функции \(y = (x-3)^2\) сдвинут на \(3\) вправо относительно графика функции \(y = x^2\).

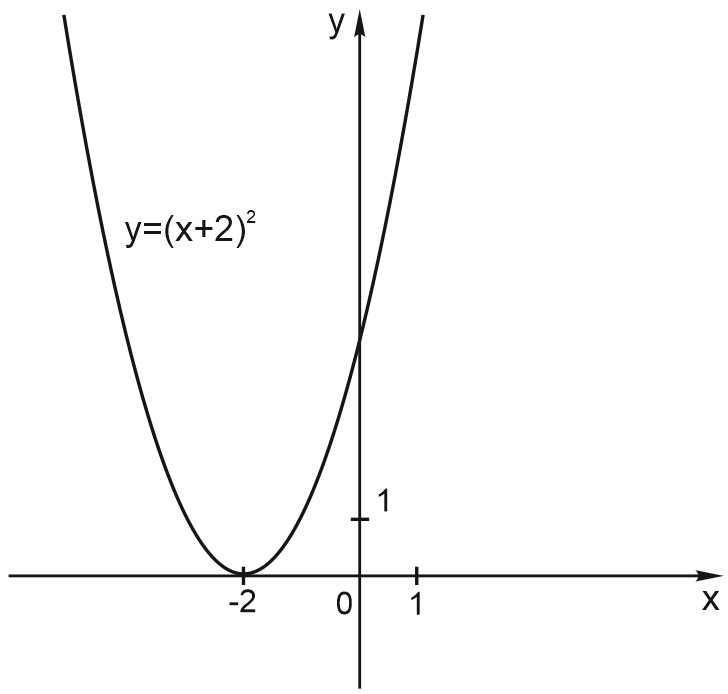
4. А график функции \(y = (x+2)^2\) сдвинут на \(2\) влево относительно графика функции \(y= x^2\).

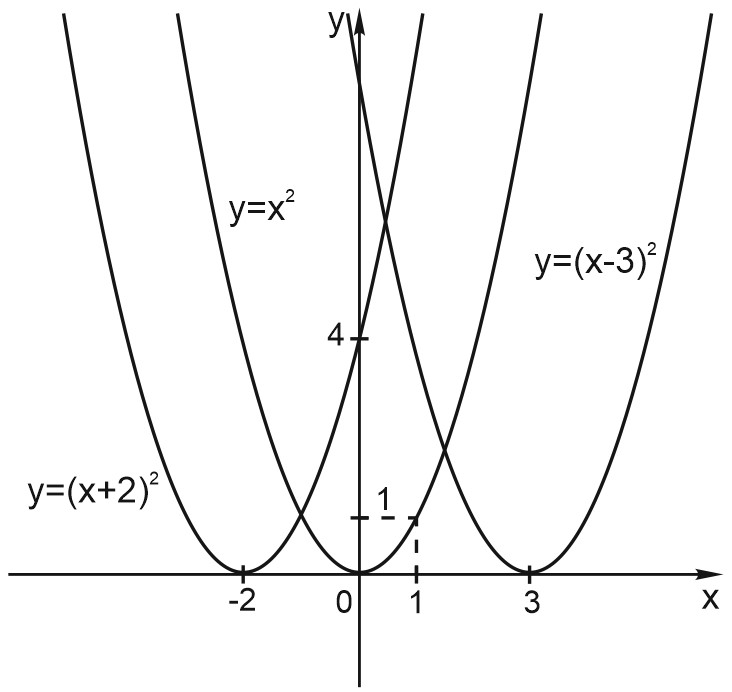
Вот что мы получили:

Если функция задана формулой \(y=(x-a)^2\) и \(a>0\), её график сдвинут относительно графика \(y= x^2\) на \(a\) вправо.

А график функции \(y=(x+a)^2\) при \(a>0\) сдвинут относительно графика функции \(y= x^2\) на \(a\) влево.

5. Построим график функции \(y = (x-3)^2 + 4\).

Он получается из графика \(y= x^2\) сдвигом на \(3\) вправо и на \(4\) вверх.

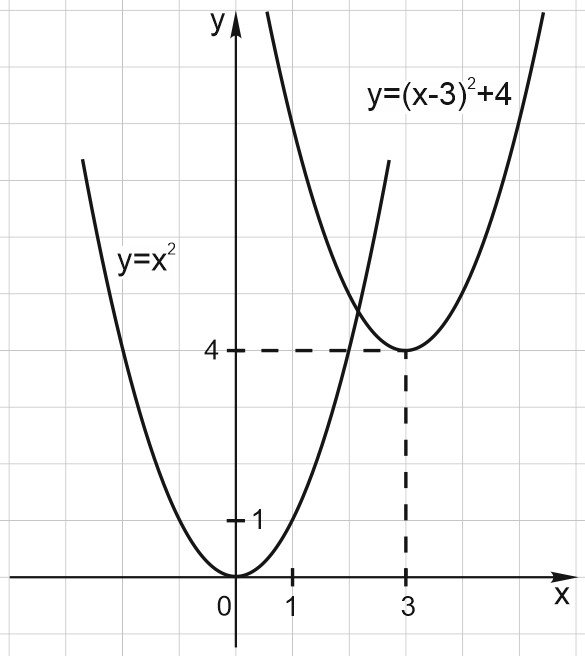
Обратите внимание, как выглядят формулы для трех функций, графики которых мы только что построили. В них есть полный квадрат!

Один из способов построения графика квадратичной функции – это выделение полного квадрата.

6. Построим график функции \(y=x^2+4x+1.\)

Выделим полный квадрат:

\(y=x^2+4x+1=x^2+4x+4-3=(x+2)^2-3.\)

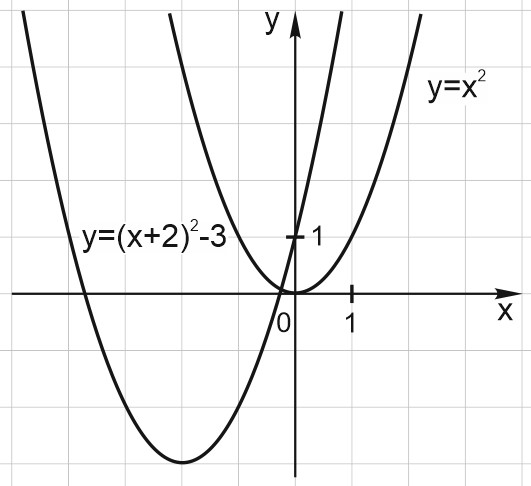
Но что делать, если не удается выделить полный квадрат? В этом случае мы строим график по следующей схеме:

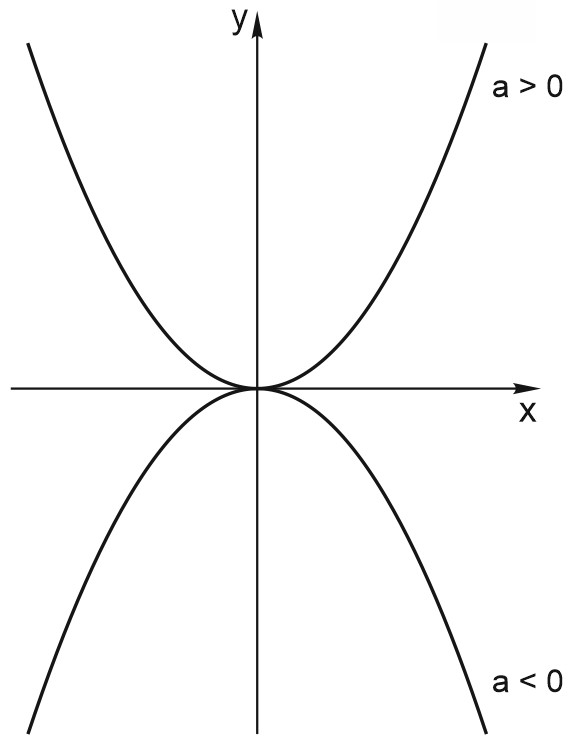
1) Смотрим на знак коэффициента \(a\).

Знак коэффициента \(a\) отвечает за направление ветвей. При \(a>0\) ветви направлены вверх, при \(a<0\)  — вниз.

На рисунке приведены две параболы \(y = ax^2\) с равными по модулю, но противоположными по знаку значениями \(a\).

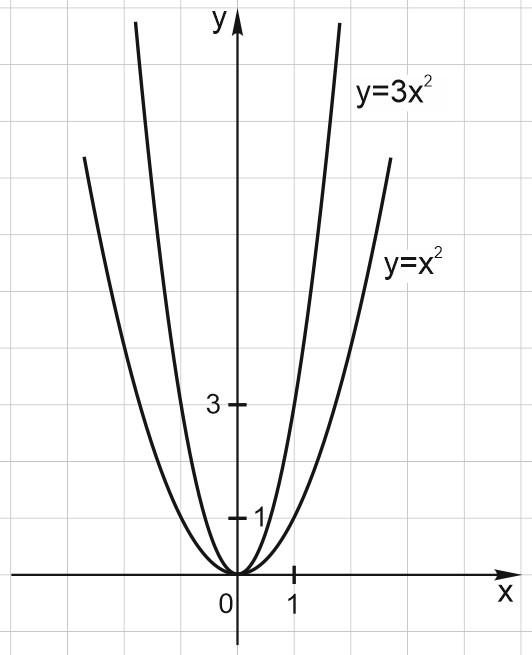
2) Абсолютная величина коэффициента \(a\) отвечает за «раскрыв» параболы. Чем больше \(\left| a\right|\), тем у́же парабола (больше прижата к оси \(Y\)). Наоборот, чем меньше \(\left| a\right|\), тем шире парабола (больше прижата к оси \(X\)).

7. На рисунке показаны две параболы \(y = x^2\) и \(y = 3x^2\).

Вторая парабола в \(3\) раза более узкая, чем первая.

3) Абсцисса вершины параболы \(y = ax^2 + bx + c\) находится по формуле:

\(x_0=-\displaystyle\frac{b}{2a}.\)

Чтобы найти ординату вершины \(y_0\), удобнее всего подставить \(x_0\) в уравнение параболы. Но вообще, полезно помнить, что

\(y_0=-\displaystyle\frac{D}{4a},\)

где \(D = b^2 - 4ac\) — дискриминант.

4) Точки пересечения параболы \(y = ax^2 + bx + c\) с осью \(X\) – это корни квадратного уравнения \(ax^2 + bx + c=0\). Если дискриминант равен нулю, то парабола касается оси \(X\). Если дискриминант меньше нуля, то корней нет, и парабола не пересекает ось \(X\).

5) Точка пересечения с осью \(Y\) находится легко: мы подставляем \(x = 0\) в уравнение параболы. Получается точка \((0; c)\).

6) И пользуемся тем, что парабола симметрична относительно прямой, проходящей через ее вершину.

8. Построить график функции: \(y=x^2-8x+12.\)

Выделим полный квадрат в формуле функции:

\(y=(x^2-8x+16)-16+12;\)

\(y=(x-4)^2-4.\)

График этой функции получим сдвигом графика функции \(y=x^2\)  вдоль оси \(X\) на \(4\) единицы вправо и вдоль оси \(Y\) на \(4\) единицы вниз.

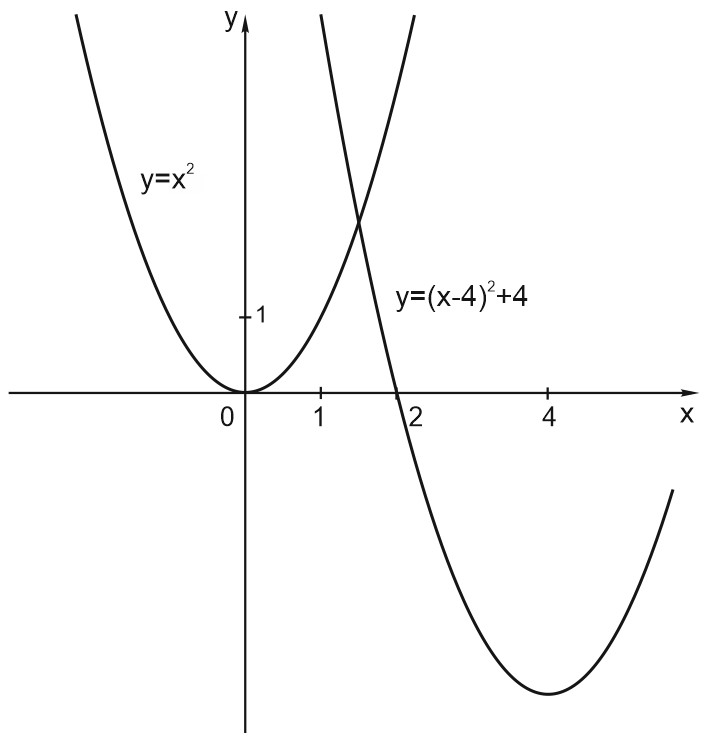
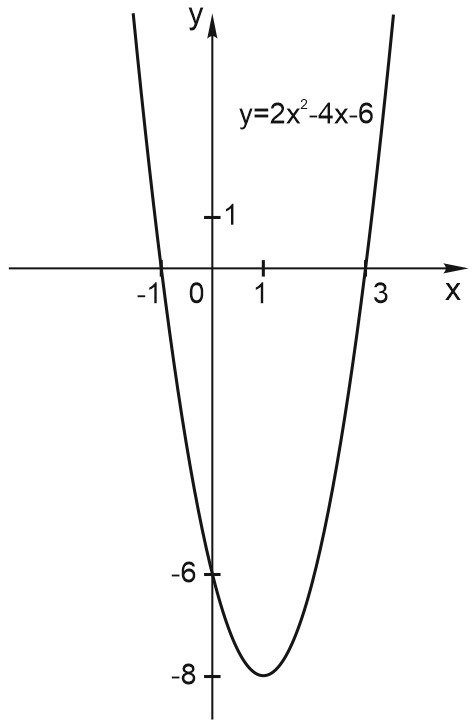
9. Построить график функции: \(y=2x^2-4x-6.\)

График этой функции построим по алгоритму, без выделения полного квадрата.

1) \(a=2>0\), значит, ветви параболы направлены вверх.

2) \(a=2\), значит, готовый график будет в два раза у́же, чем исходный \(y=x^2.\)

3) Найдем координаты вершины параболы:

\(x_0=\displaystyle\frac{-b}{2a}; \;  x_0=\displaystyle\frac{4}{4}=1;\)

\(y_0=2\cdot 1^2-4\cdot 1-6=2-4-6=-8.\)

4) Найдем точки пересечения параболы с осью \(X\):

\(2x^2-4x-6=0;\)

\(x^2-2x-3=0.\)

Корни уравнения: \(x=3\) и \(x=-1.\)

5) Найдем точку пересечения с осью \(Y\): подставляем \(x = 0\) в уравнение параболы.

\(y=0^2-4\cdot 0-6=-6.\)

Получается точка \((0; -6).\)

6) Пользуемся симметричностью графика относительно его вершины.

Примеры решения задач ОГЭ:

1. На рисунке изображены графики четырех квадратичных функций.

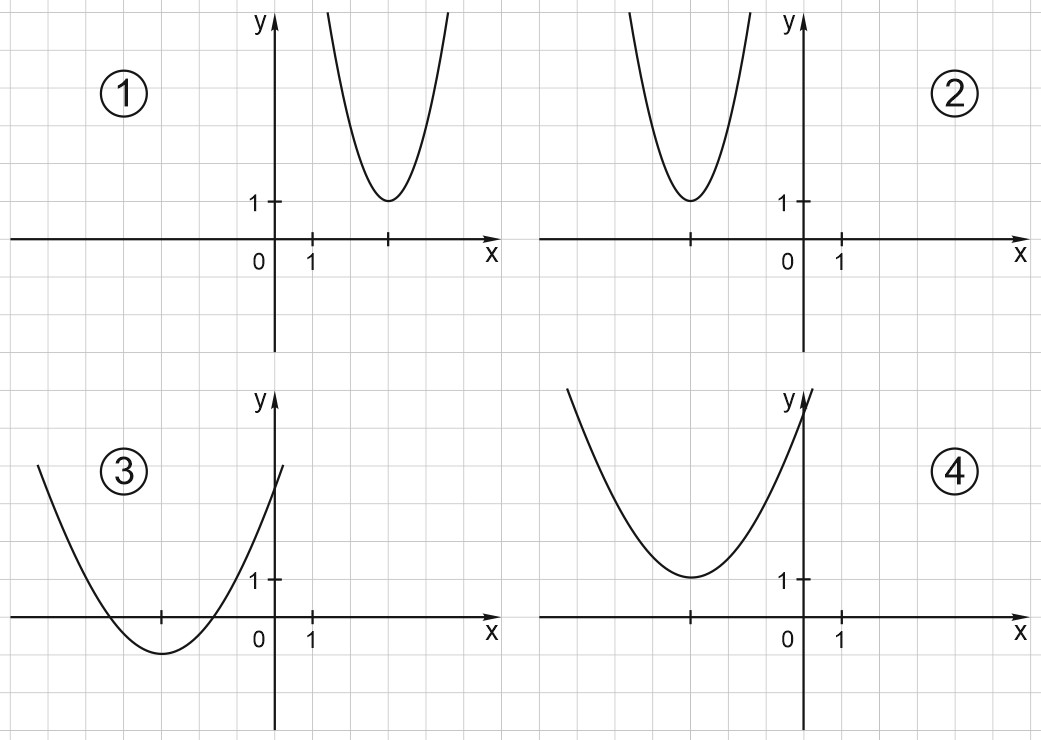
а) На каком из рисунков изображен график функции \(y=2(x+3)^2+1\)? В ответ запишите номер рисунка.

Решение:

Вершина параболы – в точке с координатами \((-3; 1)\). Парабола растянута в \(2\) раза по оси ординат. Это рисунок 2.

Ответ: 2.

б) На одном из рисунков изображен график функции \(y=0,5 (x+3)^2-1\). На каком? В ответ запишите номер рисунка.

Решение:

Вершина параболы – в точке с координатами \((-3; - 1)\). Парабола сжата в \(2\) раза по оси ординат. Это рисунок 3.

Ответ: 3

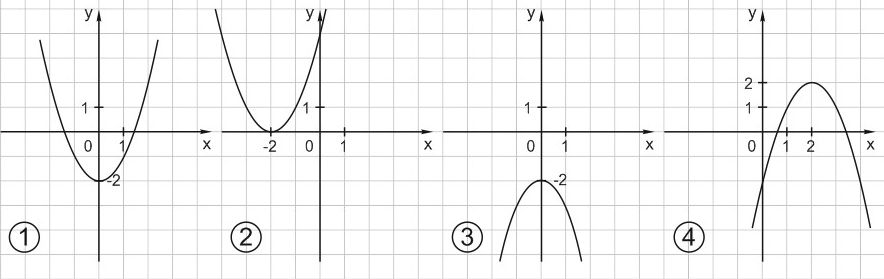
2. На каком рисунке изображен график функции \(y=-x^2-2\)?

Решение:

Формула \(y=-x^2-2\) задает параболу с ветвями вниз, полученную с помощью сдвига параболы \(y=-x^2\) на \(2\) единицы вниз вдоль оси \(OY\). Такая парабола изображена на рисунке 3.

Ответ: 3

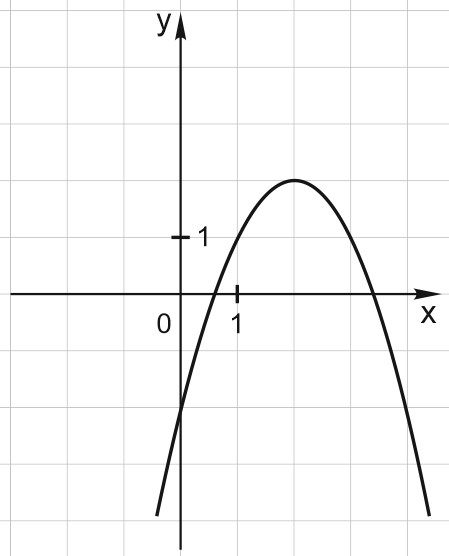
3. Определите, график какой из функций изображен на рисунке. В ответе запишите номер формулы.

1) \(y=-x^2+2;\)

2) \(y=-(x-2)^2;\)

3) \(y=-x^2-2;\)

4) \(y=-(x-2)^2+2.\)

Решение:

На рисунке изображена парабола с ветвями вниз, коэффициент при \(x^2\)  – отрицательный.

Так как вершина параболы имеет координаты \((2; 2)\), то эта парабола получена сдвигом параболы \(y=-x^2\) на \(2\) единицы вправо по горизонтали и на \(2\) единицы вверх по вертикали.

Формула функции, график которой изображен на рисунке: \(y=-(x-2)^2+2\). Это формула 4.

Ответ: 4

4. Найдите значение \(c\) по графику функции \(y=ax^2+bx+c\), изображенному на рисунке.

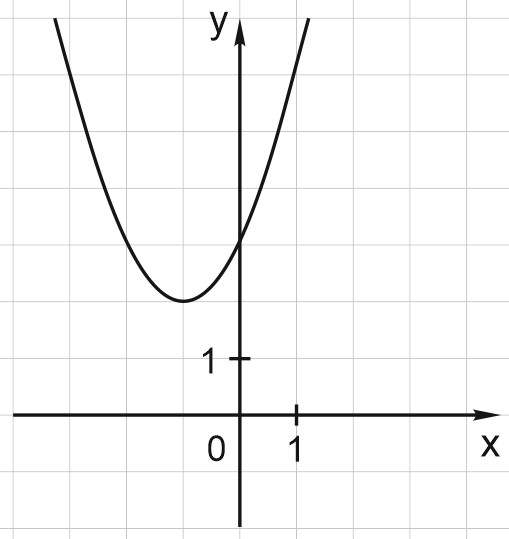
Решение:

Значение \(c\)  — это ордината графика при \(x=0\). Значит, \(c=3\).

Ответ: 3

5. На рисунке изображён график функции \(y=ax^2+bx+c\). Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

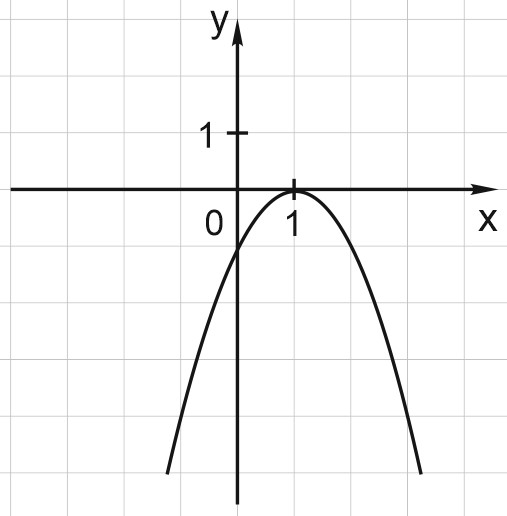
Утверждения:

А) функция возрастает на промежутке

Б) функция убывает на промежутке

Промежутки:

1) \([1; 2];\)

2) \([0; 2];\)

3) \([-1; 0];\)

4) \([-2; 3].\)

А	Б
	а

Решение:

Данная квадратичная функция возрастает на промежутке \((-\infty; 1)\). Этому промежутку соответствует единственный отрезок \([-1; 0]\), под номером 3.

И функция убывает на промежутке \((1;+\infty)\), а этому промежутку принадлежит отрезок под номером 1, то есть \([1; 2]\). Это ответ №1.

Ответ: 31

6. На рисунке изображены графики функций вида \(y=ax^2+bx+c\). Для каждого графика укажите соответствующее ему значения коэффициента \(a\) и дискриминанта \(D\).

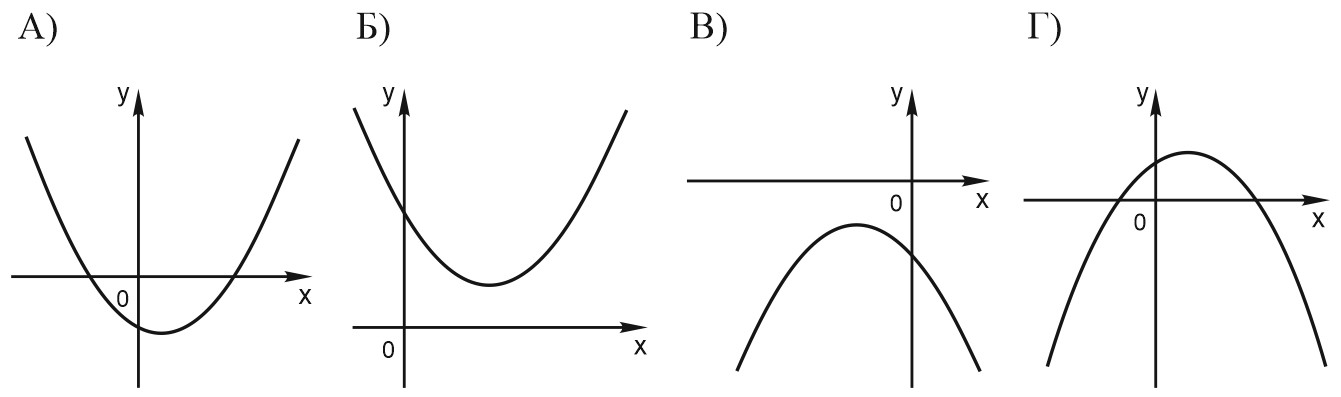
Знаки чисел:

1) \(a>0, \; D>0;\)

2) \(a>0, \; D<0;\)

3) \(a<0, \; D>0;\)

4) \(a<0, \; D<0.\)

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б	В	С
		а

Решение:

а) Ветви графика направлены вверх, значит, \(a>0\). Парабола пересекает ось \(OY\) в двух точках, значит уравнение имеет два корня, такое возможно, если \(D>0\). Номер 1.

б) Ветви графика направлены вверх, значит, \(a>0\). Парабола не пересекает ось \(OY\),  уравнение не имеет корней, если \(D<0\). Номер 2.

в) Ветви графика направлены вниз, значит, \(a<0\). Парабола не пересекает ось [mathOY\), уравнение не имеет корней, если \(D<0\). Номер 3.

г) Ветви этого графика направлены вниз, значит, \(a<0\). Парабола пересекает ось \(OY\) в двух точках, уравнение имеет два корня, если \(D>0\). Номер 4.

Ответ: 1234