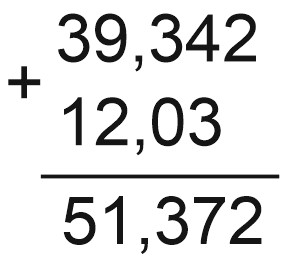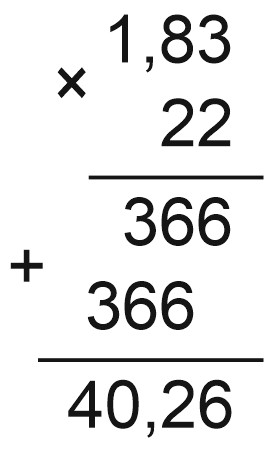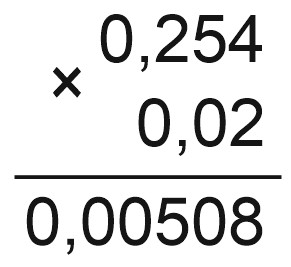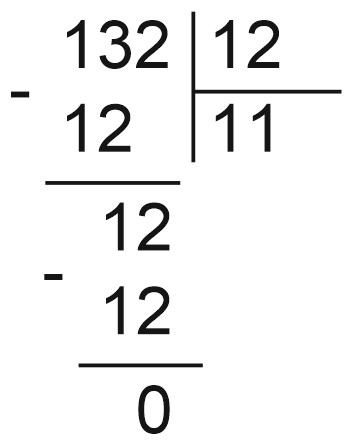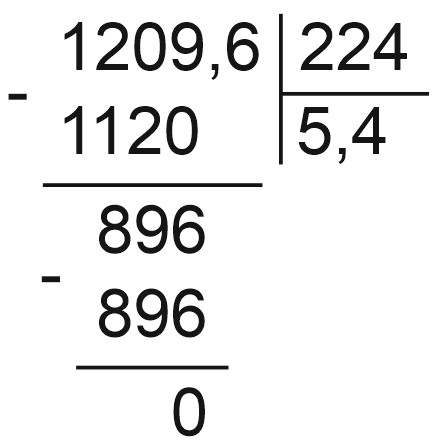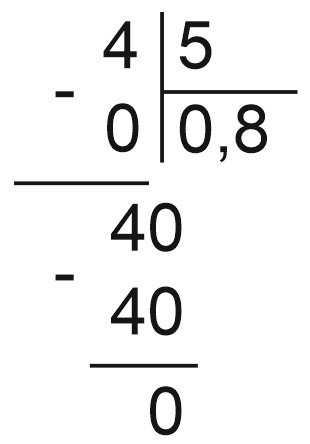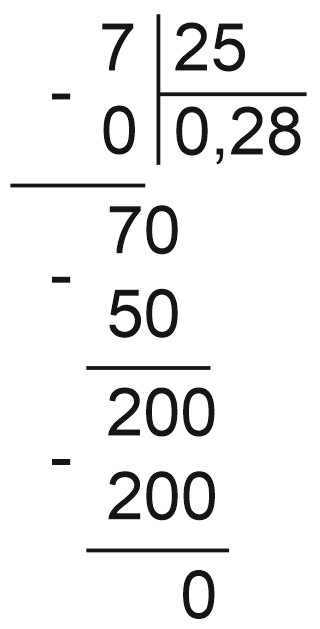Десятичные дроби

Десятичные дроби. Действия с десятичными дробями. Как перевести обыкновенную дробь в десятичную. Как перевести десятичную дробь в обыкновенную.

Числа 1,25; 3,5;  -0,75 – это десятичные дроби.

Цифры слева от запятой показывают, сколько в этом числе целых.

А цифры справа от запятой показывают, сколько в этом числе десятых, сотых или тысячных.

1,25 – это одна целая и двадцать пять сотых,

23,1 – это двадцать три целых и одна десятая,

-0,75 – это минус ноль целых и семьдесят пять сотых.

Сложение и вычитание десятичных дробей

Проще всего делать это в столбик, как мы привыкли с целыми числами. Когда мы складываем в столбик десятичные дроби, запятую ставим под запятой.

Пример 1.

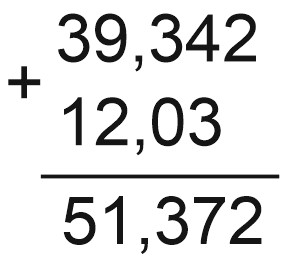
Пример 2.

\(47,52-2,5672\)

Чтобы записать вычитание столбиком, нужно дописать нули в той дроби, где их не хватает. Так, чтобы в каждой из дробей количество цифр после запятой было одинаковым

Умножение.

А при умножении столбиком десятичных дробей записываем исходные числа, выравнивая по правому краю, и здесь запятая не обязательно окажется под запятой.

Важно! Запятую в произведении надо поставить верно: считаем количество знаков после запятой у первой десятичной дроби, складываем с количеством знаков после запятой второй дроби – это и будет количеством знаков после запятой у результата.

Пример 3.

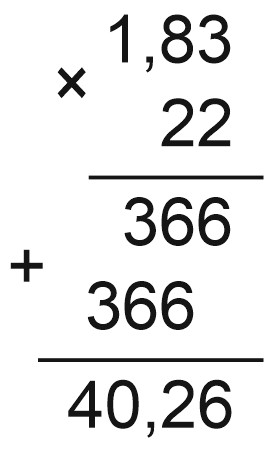
Пример 4.

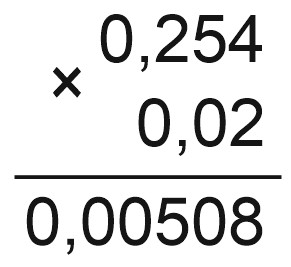
Деление.

Как поделить одну десятичную дробь на другую?

Проще всего и делимое, и делитель умножить на 10, на 100, на 1000 – на сколько нужно, чтобы делитель стал целым числом.

Напомним, что делимое - это то число, которое мы делим. А делитель - то, на что мы делим. Когда мы пишем:

\(10 : 2=5\), то 10 - делимое, 2 - делитель, 5 - частное.

Пример 5.

\(13,2 : 1,2=132 : 12=11\).

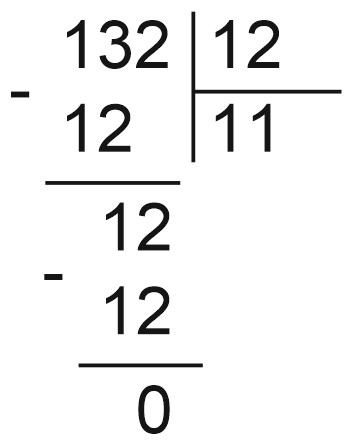
Пример 6.

\(12,096 : 2,24=1209,6 : 224=5,4\)

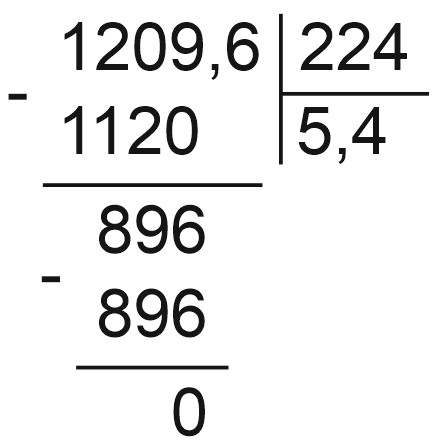
Как перевести обыкновенную дробь в десятичную, и наоборот?

Лучше всего, если у обыкновенной дроби знаменатель равен 10, 100, 1000 и т.д. Тогда она легко переводится в десятичную. Например:

\(\displaystyle \frac{15}{10}=1\frac{5}{10}=1,5\);

\(\displaystyle \frac{3}{10}=0,3\);

\(\displaystyle \frac{134}{100}=1 \frac{34}{100}=1,34\);

\(\displaystyle \frac{7}{100}=0,07\).

Посмотрим, как быстро перейти к десятичной дроби, если в знаменателе числа: 2, 4, 5, 8, 20, 25, 125. Нужно домножить числитель и знаменатель на такое число, чтобы в знаменателе получить 10, 100, 1000.

Например:

\(\displaystyle \frac{3}{4}=\frac{3\cdot 25}{4\cdot25}=\frac{75}{100}=0,75\);

\(\displaystyle \frac{2}{5}=\frac{2\cdot2}{5\cdot2}=\frac{4}{10}=0,4\);

\(\displaystyle \frac{7}{20}=\frac{7\cdot5}{20\cdot5}=\frac{35}{100}=0,35\).

Как в общем случае перевести дробь из обыкновенной в десятичную? Просто разделим в столбик числитель на знаменатель.

Пример 7. Переведем \(\displaystyle \frac{4}{5}\) в десятичную дробь, получим 0,8.

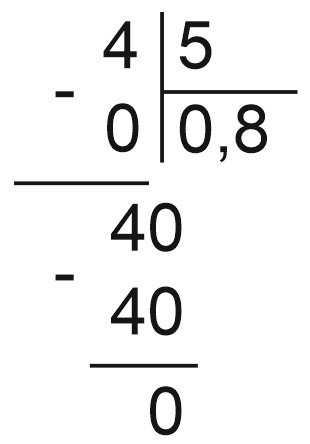
Пример 8. Переведем в десятичную дробь \(\displaystyle \frac{7}{25}\), получим 0,28.

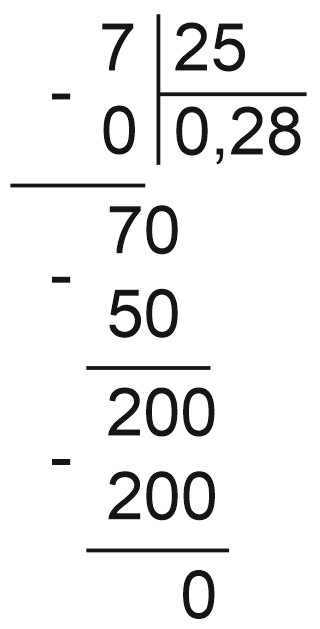
Пример 9. Переведем в десятичную дробь \(\displaystyle \frac{3}{8}\), получим 0,375.

Перевести десятичную дробь в обыкновенную еще проще. Надо записать ее в виде обыкновенной и, если возможно, сократить.

Пример 10.

\(0,8=\displaystyle \frac{8}{10}=\frac{4}{5}\).

Пример 11.

\(2,05=\displaystyle \frac{205}{100}=\frac{41}{20}\).

Напомним, что знак деления : и дробная черта -  это одно и то же.

Можно записать: \(4 : 5 = 0,8\).

А можно записать так: \(\displaystyle \frac{4}{5}=0,8\).

Примеры решения задач ОГЭ по теме: Десятичные дроби

1. Из данных обыкновенных дробей найдите те, которые можно перевести в конечную десятичную дробь. В ответ запишите номера этих дробей без пробелов и знаков препинания:

1) \(\displaystyle \frac{3}{5}\);

2) \(\displaystyle \frac{12}{7}\);

3) \(\displaystyle \frac{2}{3}\);

4) \(\displaystyle \frac{16}{25}\);

5) \(\displaystyle \frac{8}{125}\).

Решение:

Переведем каждую из десятичных дробей в обыкновенные, поделив числитель и знаменатель столбиком.

Другой способ: умножать числитель и знаменатель на такое число, чтобы получить в знаменателе 10, 100, 1000.

1) \(\displaystyle \frac{3}{5}=0,6\);

2) \(\displaystyle \frac{12}{7}=1,714285714...\) –бесконечная десятичная дробь;

3) \(\displaystyle \frac{2}{3}=0,6666...\) – бесконечная десятичная дробь;

4) \(\displaystyle \frac{16}{25}=0,64\);

5) \(\displaystyle \frac{8}{125}=0,064\).

Видим, что к конечной десятичной дроби можно привести только дроби под номерами 1,4,5.

Заметим, что любую обыкновенную дробь можно представить либо в виде конечной десятичной дроби, либо в виде бесконечной периодической десятичной дроби. Периодической – означает, что цифры или группы цифр будут повторяться бесконечно, как мы получили в пунктах (2) и (3).

Ответ: 145.

2. Найдите значение выражения: \(\displaystyle \frac{4,8\cdot 0,4}{0,6}\).

Решение:

Домножим на 10 числитель и знаменатель дроби, чтобы знаменатель стал целым.

\(\displaystyle \frac{4,8\cdot 0,4}{0,6}=\frac{4,8\cdot 0,4\cdot 10}{0,6\cdot 10}={48\cdot 0,4}{6}=8\cdot 0,4=3,2.\)