Дробно-рациональная функция. Асимптоты.

Функция \(y=\displaystyle \frac{1}{x}\). Дробно-рациональные функции.

Вспомним, как выглядит знакомый вам с 7-го класса график функции \(y=\displaystyle \frac{1}{x}\).

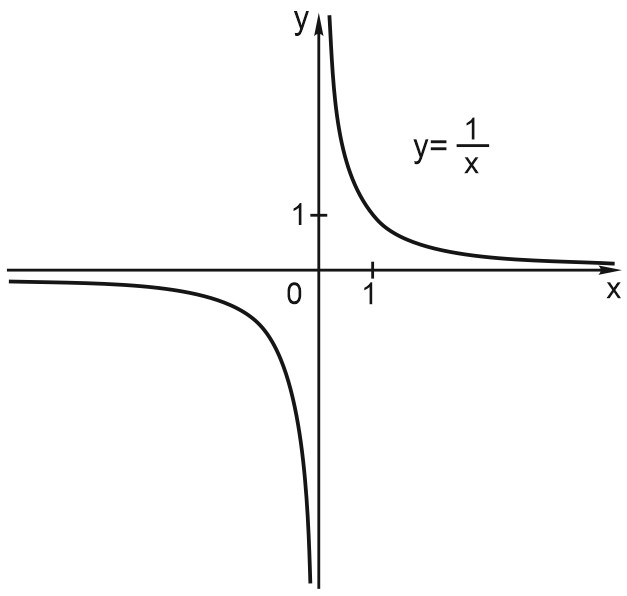
В математике такой график называется гиперболой.

Функция \(y=\displaystyle \frac{1}{x}\) не определена при \(x=0\), потому что на \(0\) делить нельзя. При всех остальных значениях \(x\) она определена.

Пусть \(x\) положителен. Будем двигаться вправо по графику, в положительном направлении оси \(X\). Увеличиваем \(x\) – уменьшается \(y\). Такая зависимость называется обратной пропорциональностью.

Чем больше \(x\), тем меньше \(\displaystyle \frac{1}{x}\).

Если \(x=10\), то \(y=\displaystyle \frac{1}{10}\).

Если \(x=100\), то \(y=\displaystyle \frac{1}{100}\).

Если \(x=10000\) , то \(y=\displaystyle \frac{1}{10000}\).

Можем ли мы получить \(y=0\)? – Нет, не можем. Потому что у уравнения \(\displaystyle \frac{1}{x}=0\)  нет решений.

Чем больше \(x\), тем ближе график функции \(y=\displaystyle \frac{1}{x}\) подходит к оси абсцисс, но не пересекает ее и не сливается с ней. Если бы график где-нибудь пересек ось \(X\), это означало бы, что есть такая точка, где \(\displaystyle \frac{1}{x}=0\), а такого быть не может.

Но и параллельно оси \(X\) график не идет. Он становится все ближе и ближе к ней. Расстояние между графиком и осью \(X\) бесконечно уменьшается, но нигде не равно нулю.

Говорят, что если \(x\) стремится к бесконечности, то \(\displaystyle \frac{1}{x}\) стремится к нулю.

Записывают это так:

Если \(x \rightarrow \infty\), то \(\displaystyle \frac{1}{x} \rightarrow 0\).

Обратите внимание: бесконечность – это не число. Когда мы говорим, что \(x\) стремится к бесконечности, это означает, что он становится больше любого, какого угодно большого числа. Больше миллиона, больше миллиарда, больше тысячи миллиардов.

При отрицательных \(x\) – симметричная картина.

Если \(x \rightarrow - \infty\), то \(\displaystyle \frac{1}{x} \rightarrow 0\).

Прямая \(y=0\), то есть ось абсцисс, - это горизонтальная асимптота для графика функции \(y=\displaystyle \frac{1}{x}\) при \(x\), стремящемся к бесконечности.

А что происходит, когда \(x\) близок к нулю, но не равен нулю?

Посмотрим на график. При положительных \(x\), близких к нулю, график резко уходит вверх, а при отрицательных \(x\), близких к нулю, - резко вниз.

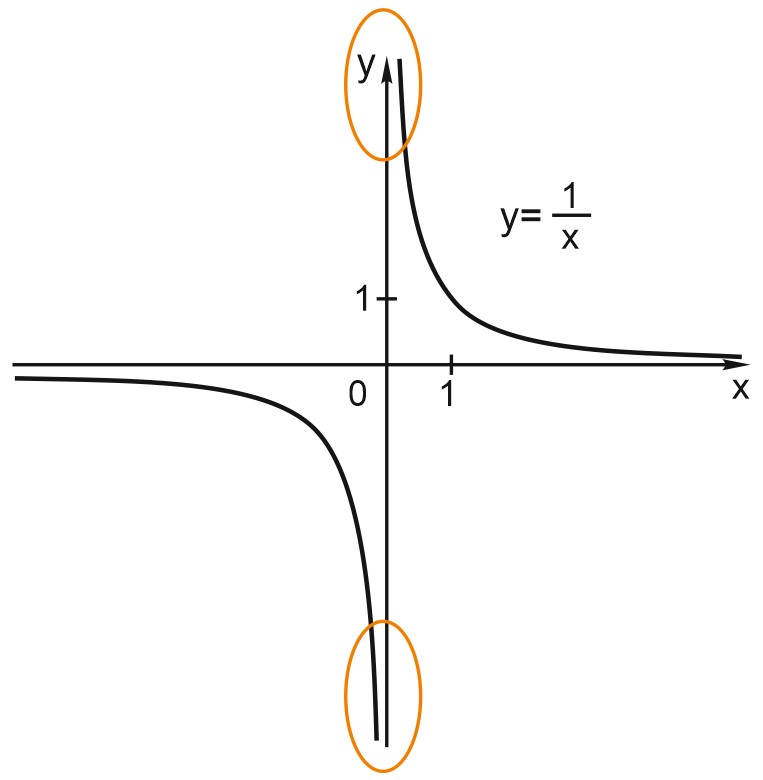
И это тоже легко объяснить.

Пусть \(x\) стремится к нулю. Это значит, что мы берем значения переменной \(x\) все меньше и меньше. И в какой-то момент увидим, что \(x\) меньше \(\displaystyle \frac{1}{100}\), меньше \(\displaystyle \frac{1}{1000}\)…

Какую бы сколь угодно малую величину мы ни взяли, \(x\) будет меньше этой величины.

Кратко это записывается так: \(x\rightarrow0\).

Тогда значение переменной \(y\) стремится к бесконечности, \(\displaystyle \frac{1}{x}\rightarrow \infty\).

Запишем кратко: Если \(x\rightarrow0\), то \(\displaystyle \frac{1}{x}\rightarrow \infty\).

Это мы и видим на графике.

В самом деле, \(1:\displaystyle \frac{1}{100}=100\), \(1:\displaystyle \frac{1}{1000}=1000\),  и чем ближе \(x\) к нулю, тем дальше в бесконечность уходит величина \(\displaystyle \frac{1}{x}\).

Прямая \(x=0\), или ось ординат, - вертикальная асимптота графика функции \(y=\displaystyle \frac{1}{x}\).

Что же такое асимптота?

Асимптота – это прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней.

Есть два варианта произнесения этого слова: асимпто́та, или аси́мптота, и оба варианта считаются правильными.

Вот на рисунке график функции и его горизонтальная асимптота \(y=3\). Чем больше \(x\), тем ближе подходит график к прямой \(y=3\).

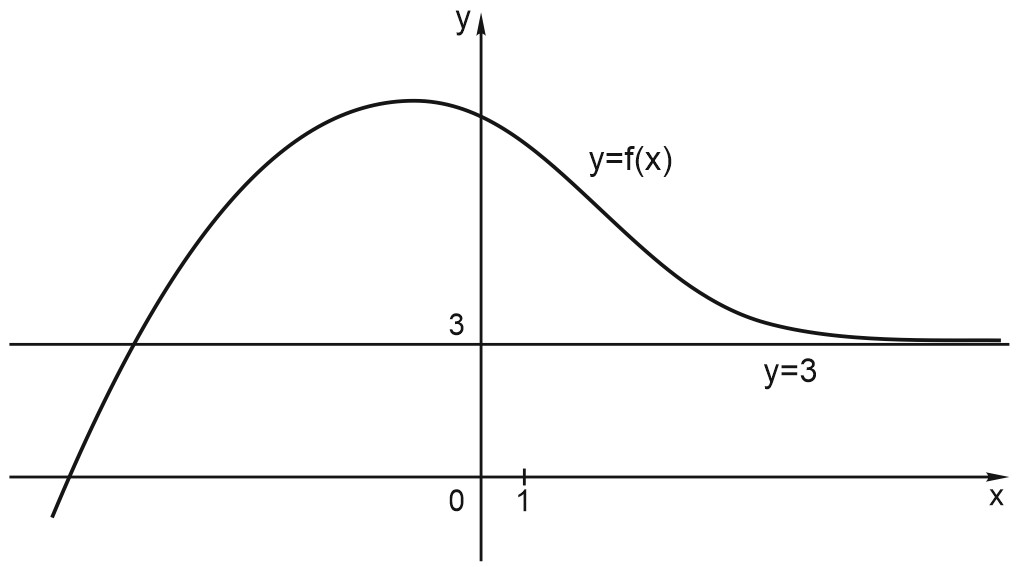
Обратите внимание: при некотором значении \(x\) график пересекает асимптоту. Да, горизонтальную асимптоту график может пересечь в какой-либо точке, но не в бесконечности.

А вертикальную асимптоту график не может пересечь никогда.

1. Построим график функции \(y=\displaystyle \frac{1}{x-2}+3\).

Решение:

Он получается из графика функции \(y=\displaystyle \frac{1}{x}\) сдвигом на \(2\) единицы вправо и на \(3\) единицы вверх. Вместе с графиком двигаются и асимптоты.

В этом случае вертикальная асимптота – это прямая \(x=2\), а горизонтальная – прямая \(y=3\).

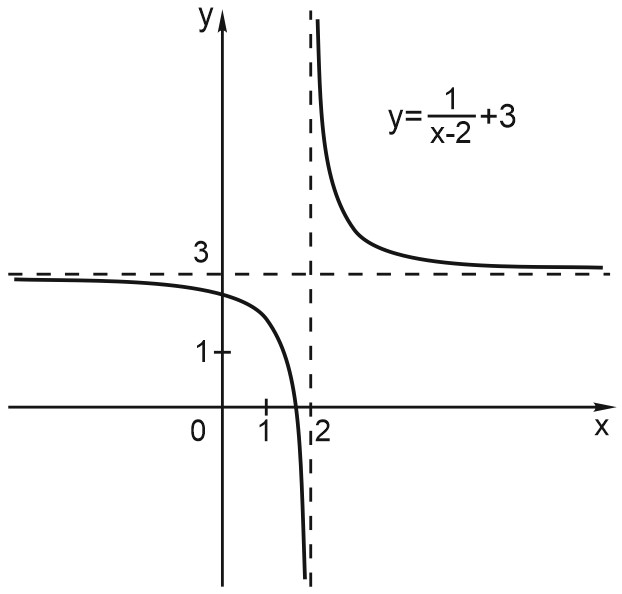
Обратим внимание, что вертикальная асимптота соответствует значению \(x=2\), при котором знаменатель обращается в ноль. В точке \(x=2\) функция \(y=\displaystyle \frac{1}{x-2}+3\) не определена.

2. Построим график функции \(y=\displaystyle \frac{2x+4}{x-3}\).

Решение:

Такая функция называется дробно-рациональной. В формуле есть дробь, в числителе и в знаменателе которой – рациональные выражения.

Но как же нам построить этот график? Если увеличивается \(x\), то и числитель, и знаменатель становятся больше. Что происходит с дробью – непонятно.

В таких случаях математики применяют полезный прием – выделение целой части.

Выделим в формуле функции целую часть.

В знаменателе \(x-3\).

Давайте в числителе выделим выражение \(k(x-3)\).

Числитель: \(2x+4= 2x-6+6+4=2(x-3)+6+4=2(x-3)+10.\)

И представим дробь в виде суммы двух дробей с одинаковыми знаменателями.

\(y=\displaystyle \frac{2x+4}{x-3}=\frac{2(x-3)+10}{x-3}=\frac{2(x-3)}{x-3}+\frac{10}{x-3}=2+\frac{10}{x-3}.\)

График функции – гипербола, сдвинутая на \(3\) вправо по \(x\) и на \(2\) вверх по \(y\) и растянутая в \(10\) раз по сравнению с графиком функции \(y=\displaystyle \frac{1}{x}\).

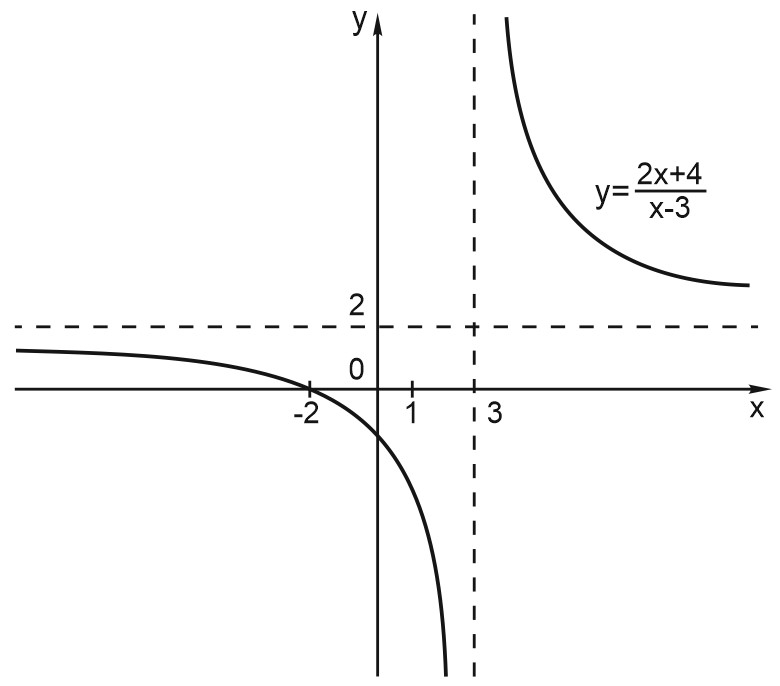
Обратите внимание: вертикальная асимптота графика \(x= 3\) соответствует точке, в которой функция не определена.

Но всегда ли точка, в которой функция не определена, соответствует вертикальной асимптоте?

3. Рассмотрим функцию \(y=\displaystyle \frac{x^2-9}{x-3}\). Будет ли у нее вертикальная асимптота \(x=3\)?

Решение:

Чтобы ответить на этот вопрос, разложим выражение в числителе по формуле разности квадратов.

Получим: \(y=\displaystyle \frac{(x-3)(x+3)}{x-3}=x+3\) при \(x\neq3\).

Никаких вертикальных асимптот здесь нет.

График – прямая \(y= x + 3\), причем точка с абсциссой \(3\) на этой прямой – выколотая.

Часто при построении графиков мы начинаем с преобразования формулы функции. Выделяем полные квадраты, применяем формулы сокращенного умножения, выделяем целую часть. Давайте потренируемся это делать.

Выделение целой части

4. Выделим целую часть дроби \(\displaystyle \frac{x^2-2x+3}{x-1}\).

Решение:

\(\displaystyle \frac{x^2-2x+3}{x-1}=\frac{x^2-2x+1+2}{x-1}=\frac{(x-1)^2+2}{x-1}=\frac{(x-1)^2}{x-1}+\frac{2}{x-1}=x-1+\frac{2}{x-1}\).

5. Выделите целую часть дроби.

a) \(\displaystyle \frac{a^2-4a-7}{(a-2)^2};\)

б) \(\displaystyle \frac{x^2+6x+14}{x+3}.\)

Решение:

а) \(\displaystyle \frac{a^2-4a-7}{(a-2)^2} =\frac{a^2-4a+4-4-7}{(a-2)^2} =\frac{(a-2)^2-11}{(a-2)^2} =\frac{(a-2)^2}{(a-2)^2} -\frac{11}{(a-2)^2} =1-\frac{11}{(a-2)^2}\).

б) \(\displaystyle \frac{x^2+6x+14}{x+3}=\frac{x^2+6x+9-9+14}{x+3}=\frac{(x+3)^2+5}{x+3}=\frac{(x+3)^2}{x+3}+\frac{5}{x+3}=x+3+ \frac{5}{x+3}\).

Графики дробно-рациональных функций. Схема построения графика функции.

6. Построим график функции \(y=\displaystyle \frac{3x+1}{x-2}\).

Решение:

Область определения функции: \(x\neq2\).

Выделим целую часть в формуле функции.

\(y=\displaystyle \frac{3x+1}{x-2}=\frac{3x-6+7}{x-2}=3+\frac{7}{x-2}\).

График функции \(y=\displaystyle \frac{3x+1}{x-2}\) получается из графика \(y=\displaystyle \frac{7}{x}\) сдвигом на \(2\) единицы вправо и на \(3\) единицы вверх.

Значит, \(x=2\) – вертикальная асимптота,

\(y=3\) – горизонтальная асимптота.

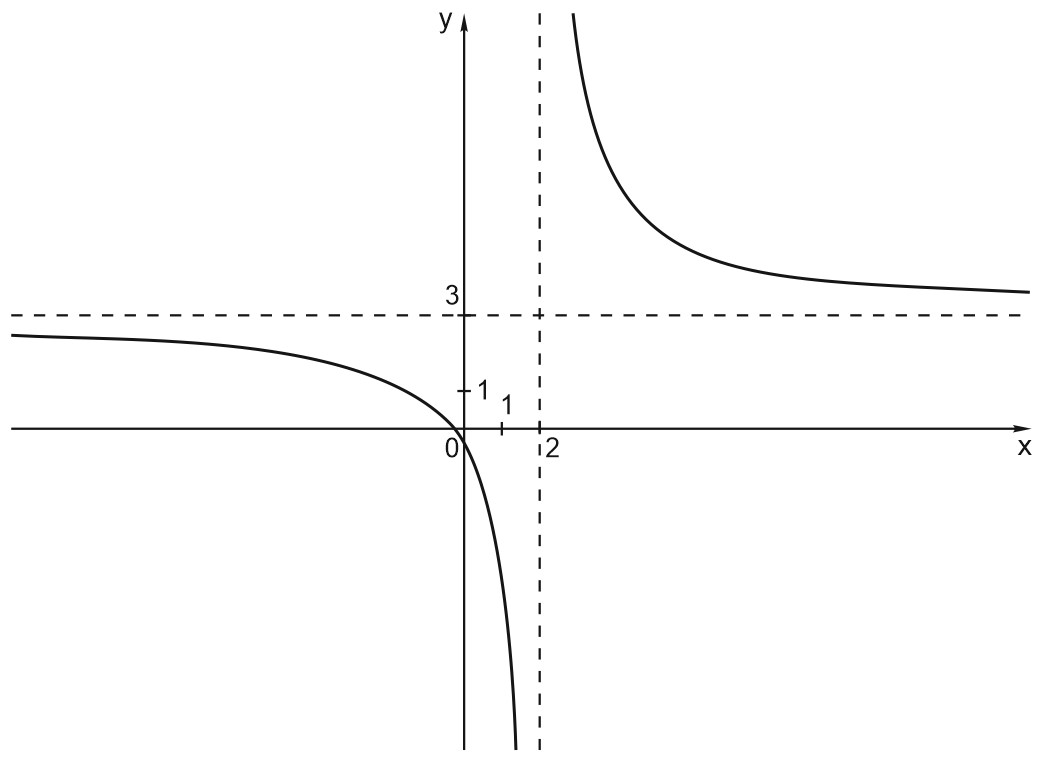
Схема построения графиков функций

Для построения сложных графиков мы применяем схему исследования функции.

Вот какие пункты она включает:

1) Область определения функции.

2) Область значений функции (если мы можем сразу ее найти).

3) Нули функции (если есть).

4) Точка пересечения с осью \(Y\) (если есть).

5) Знаки функции на интервалах. Другими словам, интервалы знакопостоянства.

6) Асимптоты (если есть).

7) Интервалы возрастания и убывания.

Следующие 2 графика – повышенной сложности. Зато на них наглядно видно, как работает метод интервалов: дробно-рациональная функция может менять знак только в тех точках, где она равна нулю или не существует.

Следующие графики – немного сложнее, чем в реальных вариантах ОГЭ.

7. Построим график функции \(y=\displaystyle \frac{2(x-1)(x+5)}{x(x-3)}\).

Решение:

Воспользуемся схемой построения графика функции.

1) Область определения: \(x\neq0\), \(x\neq3\), потому что знаменатель не должен быть равен нулю.

Область значений функции не получается найти сразу. Явных ограничений нет. Пропускаем этот пункт.

2) Нули функции: \(y=0\), если \(x=1\); \(x=-5\). Отметим на координатной плоскости точки \((1; 0)\) и \((-5; 0)\).  Отметим также точки \(0\) и \(3\). В них функция не определена, то есть не существует.

3) Точки \(-5; 0; 1; 3\) разбивают числовую прямую на интервалы. Определим знаки функции на этих интервалах. Так же, как мы делали при решении неравенств методом интервалов.

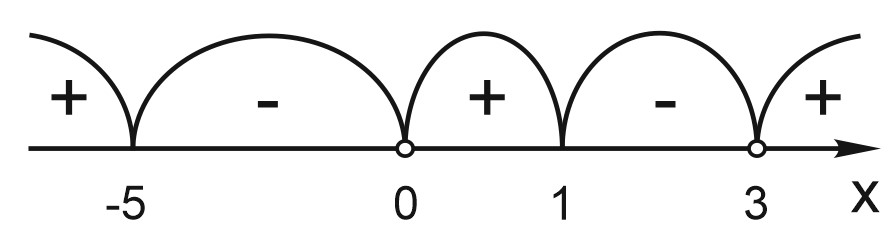
4) У нашей функции есть вертикальные асимптоты: \(x=0\); \(x=3\). В этих точках функция не определена.

5) Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда \(x\) стремится к бесконечности.

Раскроем скобки в формуле функции и выделим целую часть:

\(y=\displaystyle \frac{2(x-1)(x+5)}{x(x-3)}=\frac{2x^2+8x-10}{x^2-3x}=\frac{2x^2-6x+14x-10}{x^2-3x}=2+\frac{14x-10}{x^2-3x}\).

Осталось исследовать, как ведет себя выражение \(\displaystyle \frac{14x-10}{x^2-3x}\), если \(x\) стремится к бесконечности.

Разделим числитель и знаменатель этой дроби на \(x^2\). Мы можем это сделать, потому что если \(x\) стремится к бесконечности, то он точно не равен нулю.

Получим: \(\displaystyle \frac{\frac{14}{x}-\frac{10}{x^2}}{1-\frac{3}{x}}\).

Если \(x\rightarrow \infty \), то \(\displaystyle \frac{1}{x}\rightarrow0\). Значит, числитель этой дроби стремится к нулю, а знаменатель к \(1\), и вся дробь стремится к нулю.

Тогда \(y\rightarrow 2\). Значит, \(y=2\) — горизонтальная асимптота.

Вот эскиз графика: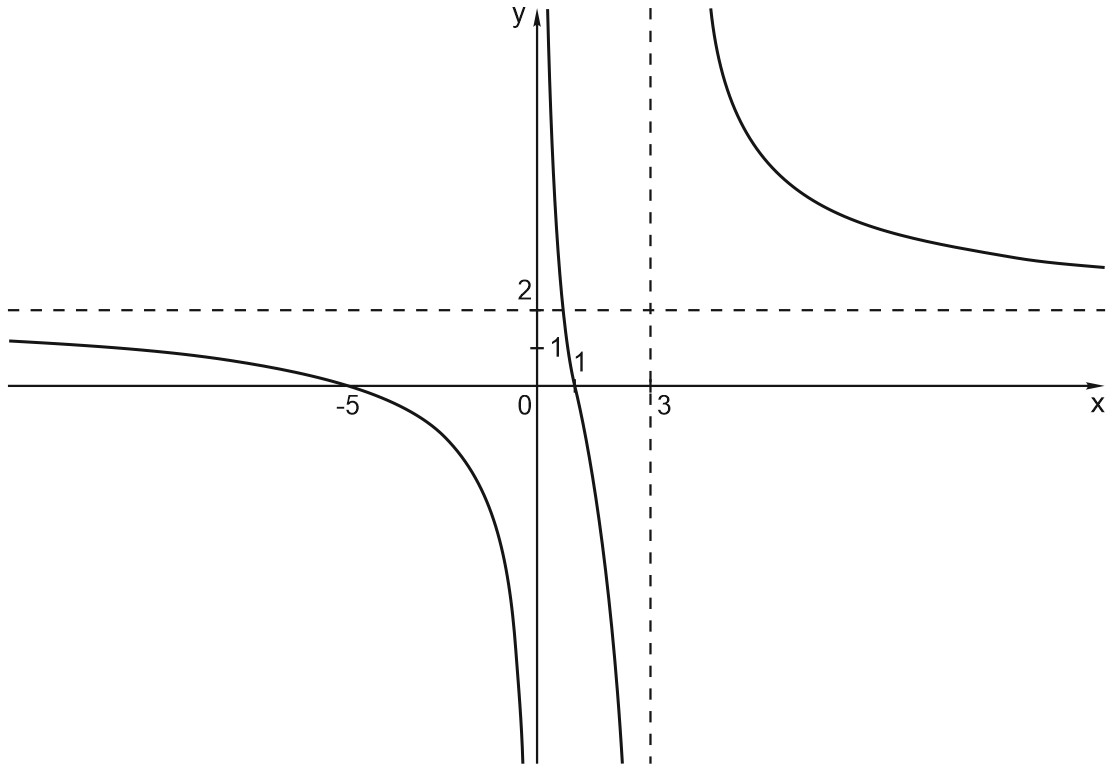 

Как мы его нарисовали?

Мы отметили нули функции и асимптоты. Расставили знаки на интервалах (плюсы и минусы). Показали, как график ближе и ближе подходит к асимптотам.

Например, при \(x>3\) значения функции положительны.

При \(x\rightarrow3\) график функции подходит справа ближе и ближе к вертикальной асимптоте \(x=3\), то есть уходит в \(+\infty. \)

При \(x\rightarrow \infty \) график функции подходит ближе и ближе к горизонтальной асимптоте \(y=2\).

Так мы и строим график на каждом участке.

Следующий график можно встретить в заданиях 2 части ОГЭ.

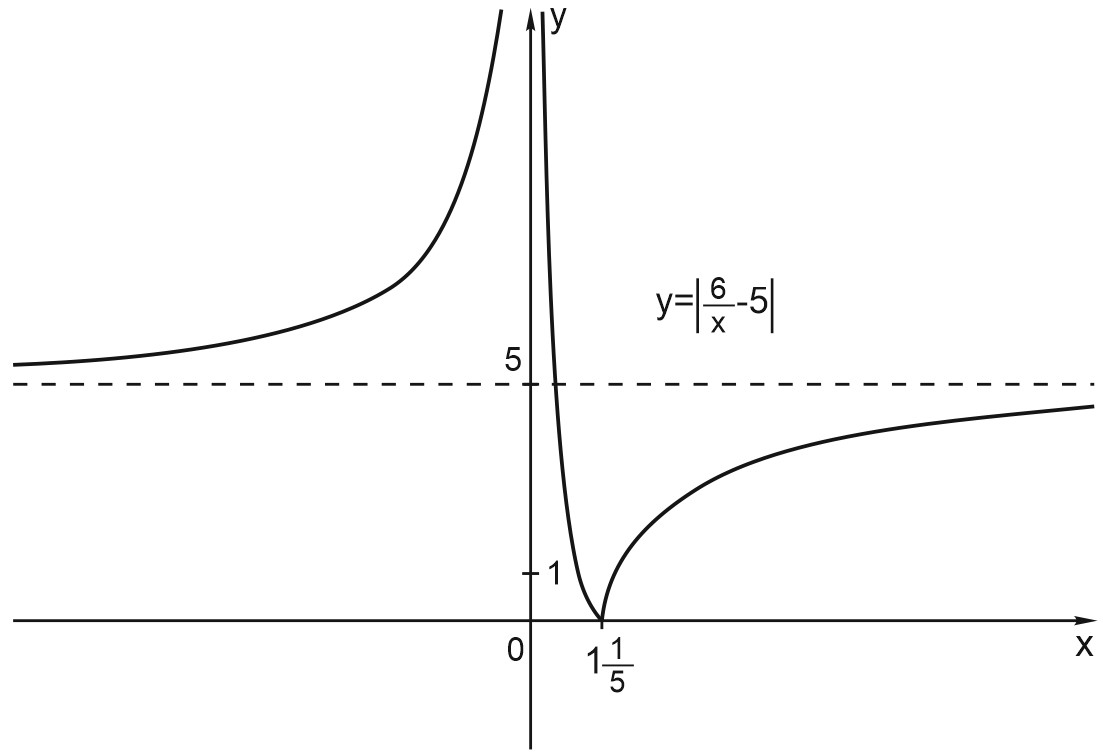
8. Построим график функции \(y=\left|\displaystyle \frac{6}{x}-5\right |\).

Решение:

Ее график получается из графика функции \(y=\displaystyle \frac{6}{x}\) сдвигом на \(5\) единиц вниз вдоль оси \(OY\) и симметричным отображением части графика, лежащей ниже оси \(OX\), в верхнюю полуплоскость.

\(x=0\) – вертикальная асимптота графика;

\(y=5\) - горизонтальная асимптота.

Примеры решения задач:

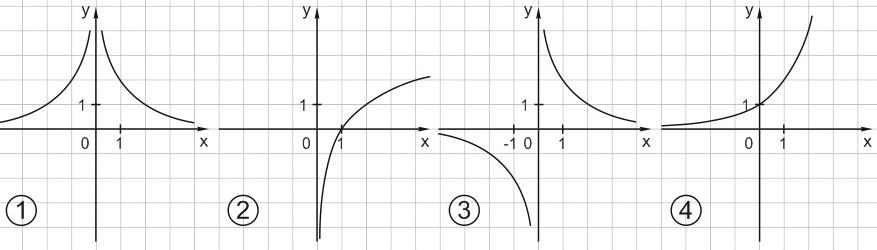
1. Определите, на каком из рисунков изображен график функции \(y=\displaystyle \frac{2}{x}\).

Решение:

Формула \(y=\displaystyle \frac{2}{x}\) задает гиперболу, расположенную в первой и третьей координатных четвертях.

Это рисунок 3.

Ответ: 3

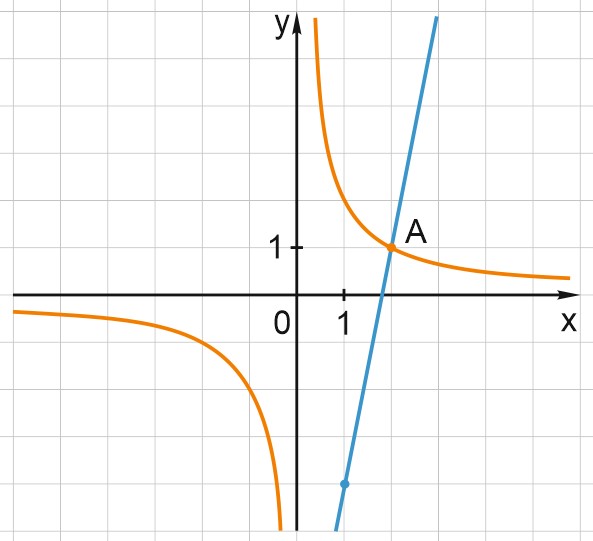
2. На рисунке изображены графики функций \(f(x)=\displaystyle \frac{k}{x}\) и \(g(x)=ax+b\), которые пересекаются в точках \(A\) и \(B\). Найдите абсциссу точки \(B\).

Решение:

График функции \(y=\displaystyle \frac{k}{x}\) проходит через точку \((2; 1)\); значит, \(\displaystyle \frac{k}{2}=1; \;k=2,\; f(x)=\frac{2}{x}.\)

График функции \(g(x)=ax+b\) проходит через точки \((2; 1)\) и \((1; -4)\), \(a=5\) – угловой коэффициент прямой.

Находим как тангенс угла наклона прямой к положительному направлению оси \(X\).

Тогда \(5\cdot2+b=1\); \(b=-9\).

Для точек \(A\) и \(B\) имеем: \(f(x)=g(x)\);

\(\displaystyle \frac{2}{x}=5x-9\);

\(5x^2-9x-2=0\).

Отсюда \(x=2\) (абсцисса точки \(A\)) или \(x=-0,2\) (абсцисса точки \(B\)).

Ответ: -0,2

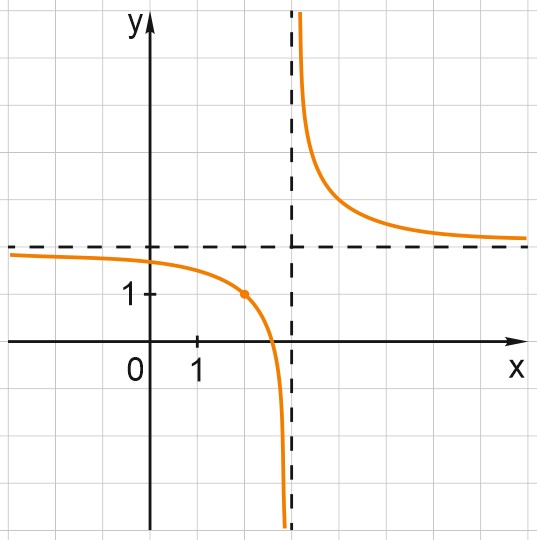
3. На рисунке изображён график функции вида \(f(x)=\displaystyle \frac{ax+b}{x+c}\), где числа \(a\), \(b\) и \(c\) - целые. Найдите \(b\).

Решение:

Посмотрим, какая функция изображена на рисунке.

График функции \(f(x)\) сдвинут на \(2\) вверх по отношению к графику функции \(y=\displaystyle \frac{1}{x}\); горизонтальная асимптота \(y=2\).

Функция не определена при \(x=3\), график сдвинут вправо на \(3\) по отношению к графику функции \(y=\displaystyle \frac{1}{x}\); вертикальная асимптота \(x=3\).

Получили: \(f(x)=\displaystyle \frac{k}{x-3}+2\).

Найдем \(k\), учитывая, что график функции \(f(x)\) проходит через точку \((2; 1)\).

\(\displaystyle \frac{k}{2-3}+2=1\), \(k = 1\).

Формула функции: \(f(x)=\displaystyle \frac{1}{x-3}+2=\frac{2x-5}{x-3}\) (привели к одному знаменателю).

Сравним с формулой функции \(f(x)=\displaystyle \frac{ax+b}{x+c}\).

Получим, что \(b=-5\).

Ответ: -5