Геометрия. Основные понятия и обозначения.

Мы начинаем изучение геометрии с основных понятий и обозначений.

Мы помним, что геометрия работает не только с числами и уравнениями, но и с геометрическими фигурами. Например: точка, прямая, отрезок…

Определим, что такое точка. Это легко, скажете вы. Точка – это вот: \(\cdot\)

Причем у нее нет ни длины, ни ширины, ни высоты.

А прямая – это вот:

Она бесконечная в обе стороны, а толщины у нее нет.

Через любые две точки можно провести прямую, причем только одну.

А луч – это часть прямой, бесконечный в одну сторону. Начало у него есть, а конца нет.

А отрезок – часть прямой. Из прямой вырезали кусочек.

Но вот какая странная вещь.

Вы заметили, что основные понятия геометрии – точку и прямую – мы не определили словами, а показали. Вот, смотрите, это прямая!

Когда-то, в Древней Греции, вся геометрия была именно такой. И доказательства были такими. Древние греки рисовали чертеж и говорили: «Смотри!» А объяснения появились позже.

Решая задачу по геометрии, мы тоже сначала смотрим на чертеж. Достраиваем на нем что-нибудь. А потом пишем доказательство или решение.

Для этого мы применяем специальный геометрический язык.

Вот какие символы мы будем использовать:

\(\parallel\) Параллельно. Когда мы пишем: \(a\parallel b\) - это означает, что прямая \(a\) параллельна прямой \(b\).

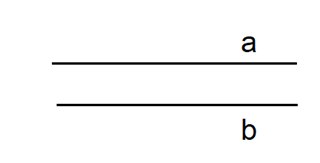
\(\cap\)  Пересекаются. Например, запись  \(a\cap b=C\) читается так: прямая \(a\)  пересекается с прямой \(b\) в точке \(C\).

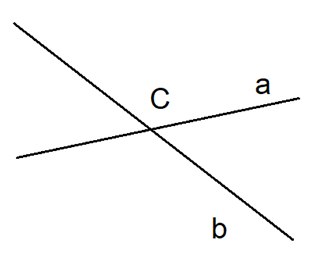
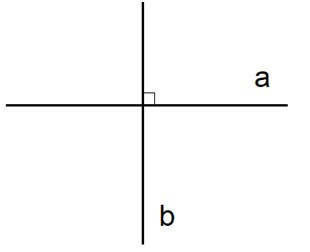
\(\perp\)  Перпендикулярно. Запись \(a \perp b\) означает, что прямые \(a\) и \(b\) пересекаются под прямым углом, то есть \(a\) и \(b\) перпендикулярны.

\(\in \) Принадлежит. Запись \(M\in a\) означает, что точка \(M\)  принадлежит прямой \(a\), то есть лежит на прямой \(a\).

Этот символ вам знаком, мы и в неравенствах так писали: \(x\in (-\infty ;-5)\).

\([AB]\) – отрезок \(AB\);

\([AB)\) – луч \(AB\);

\((AB)\) – прямая \(AB\). Обычно мы пишем просто \(AB\), без скобочек.

\(\Rightarrow\) Следовательно. Такая стрелочка означает «следует». Из одного высказывания следует другое. Примеры мы увидим.

Параллельные и перпендикулярные прямые.

Параллельные прямые

Прямые на плоскости могут быть параллельными, или пересекаться, или совпадать. И других вариантов у них нет.

Вот это – две параллельные прямые. Они не пересекаются. Нигде. Никогда. Как рельсы, по которым идет поезд.

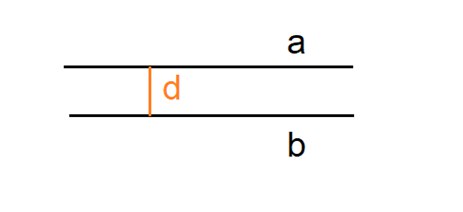
Можно сказать, что они находятся на одинаковом расстоянии друг от друга. И найти это расстояние легко: это длина отрезка, перпендикулярного обеим прямым.

Расстояние между параллельными прямыми – это длина общего перпендикуляра к ним.

Если две прямые параллельны третьей, то они параллельны между собой.

Кратко это записывается так:

\(\left.\begin{matrix}
a\parallel b \\ b\parallel c
\end{matrix}\right\} \Rightarrow a\parallel c.\)

Вот мы и применили значок  \(\Rightarrow\).

Можно сказать, что он заменяет слово «значит». Или слово «следовательно».

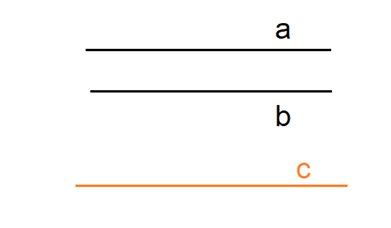
Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, причем только одну.

Вот на рисунке прямая \(b\) проведена через точку \(M\) параллельно прямой \(a\). И другую прямую, параллельную прямой \(a\), через точку \(M\) мы провести не можем. Потому что это будет не другая прямая, а та же самая прямая \(b\), то есть новая прямая и \(b\) будут совпадать.

Перпендикулярные прямые

Это – пересекающиеся прямые.

А это – перпендикулярные прямые. Они пересекаются под прямым углом.

Из любой точки, не лежащей на прямой, можно провести перпендикуляр к данной прямой.

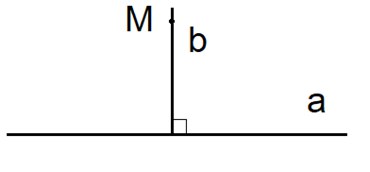
На рисунке из точки \(M\) мы провели перпендикуляр \(b\) к прямой \(a\).

Расстояние от точки до прямой – это длина перпендикуляра, проведенного из точки на прямую.

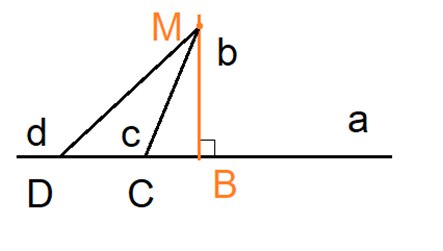
На рисунке через точку \(M\) проведены перпендикуляр \(b\) к прямой \(a\), и еще две прямые \(c\) и \(d\), которые пересекают прямую \(a\), но не перпендикулярны ей. Самый короткий путь от точки \(M\) до прямой \(a\) – это длина отрезка \(BM\), то есть длина перпендикуляра.

\(MB < MC, \; MB < MD\).

Можно сказать кратко: перпендикуляр короче наклонной.

Здесь \(MC\) и \(MD\) – наклонные к прямой \(a\).

Два перпендикуляра, проведенные к одной прямой, параллельны.

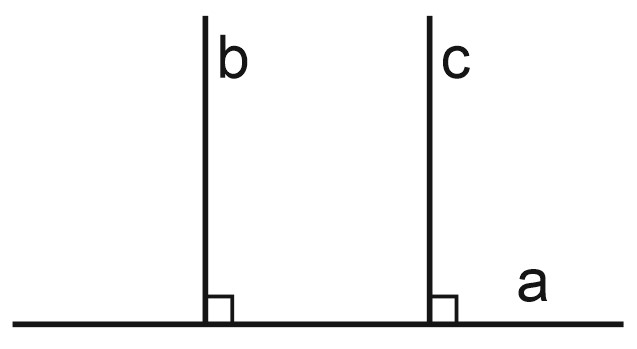
Запишем это кратко:

\(\left.\begin{matrix}
b\perp  a \\ c\perp a
\end{matrix}\right\} \Rightarrow b\perp  c.\)

Углы

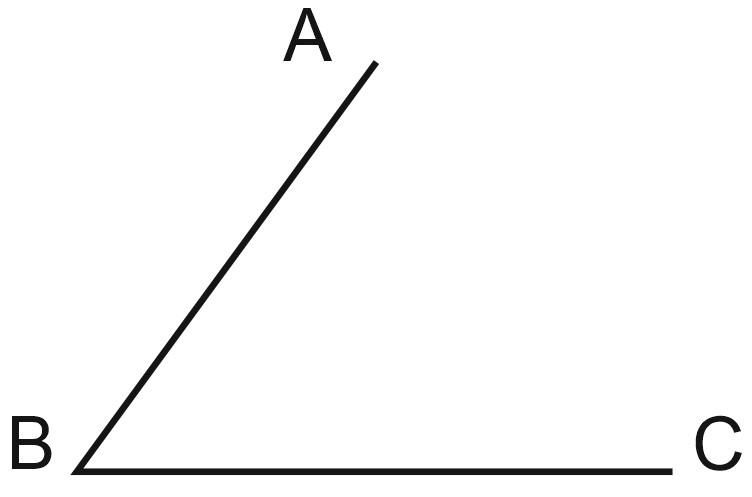
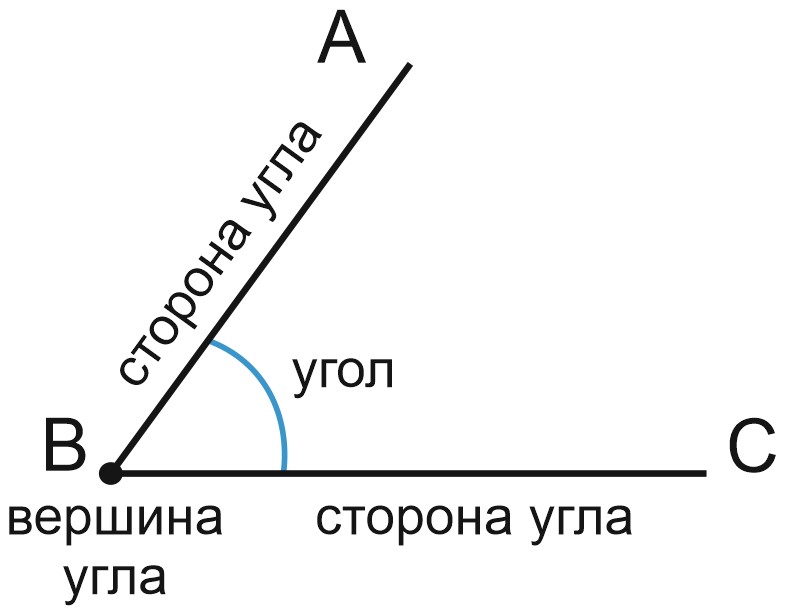
Угол – это геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

На рисунке лучи \(BA\) и \(BC\) – стороны угла. Точка \(B\) – это вершина угла. Обозначается: \(\angle ABC\).  Средняя буква в обозначении – это вершина угла.

Принято измерять углы в градусах. Есть и другая система измерения углов, радианы. О ней вы узнаете в 10-11 классах.

Полный круг равен \(360\) градусам.

Это немного необычно для нас: мы привыкли, что в килограмме \(1000\) граммов, в метре \(100\) сантиметров. Но оказывается, что в древности люди пользовались, кроме десятичной, и такой системой счисления, где числа кратны \(12\). Даже в русском языке осталось слово «дюжина», означающее \(12\).

Вот как считали дюжинами:

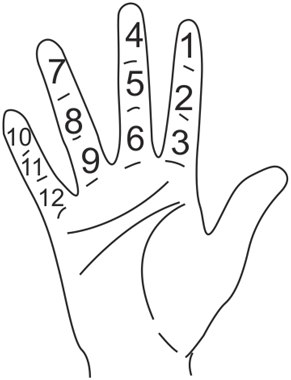
В часе 60 минут, в минуте 60 секунд. Эти числа делятся на \(12\). Есть гипотеза, что появление чисел \(60\) и \(360\) в математике древних шумеров связано с астрономией. Например, с периодом обращения Юпитера вокруг Земли (12 лет) и Сатурна (60 лет).

А есть и более простое объяснение. У числа \(360\) много делителей. Оно делится на 2, на 3, на 4, 5, 6, 8, 10, 12, 15… Круг, в котором \(360\) градусов, легко делить на части.

Один градус – это \(\displaystyle\frac{1}{360}\) часть полного круга.

И тогда половина полного круга – это \(180\) градусов. Такой угол называют развернутым. Его стороны лежат на одной прямой.

Прямой угол равен половине развернутого. Прямой угол составляет \(90\) градусов.

Острый угол меньше прямого, а тупой угол больше прямого, но меньше развернутого.

В задачах мы будем определять «на глаз», какой угол перед нами: тупой или острый. И при построении чертежей тоже важно рисовать угол таким, каким он указан в условии задачи: прямым, тупым или острым.

1. Смежные углы

Возьмем два карандаша. Один карандаш (черный) будет изображать развернутый угол, а другой (зеленый) «втыкается» в развернутый угол.

Получим чертеж:

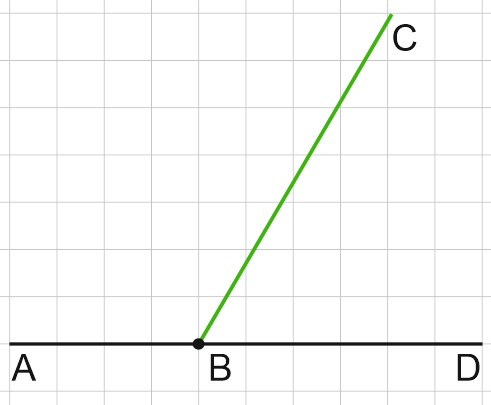
Какие геометрические конструкции мы видим? Здесь есть:

- развернутый угол \(ABD\);

- тупой угол \(ABC\);

- острый угол \(CBD\).

Мы видим, что развернутый угол \(ABD\) состоит из двух углов:

\(\angle ABD=\angle ABC+ \angle CBD=180^{\circ}.\)

Луч \(BC\) является границей между углами \(ABC\) и \(CBD\). Такие углы называют смежными.

Определение: Смежные углы – это два угла, у которых одна сторона общая, а две другие стороны образуют развернутый угол. Сумма смежных углов равна \(180^{\circ}.\).

Со смежными углами разобрались. Опустим зеленый карандаш ниже, чтобы получились две пересекающиеся прямые. Получим новый чертеж.

2. Вертикальные углы

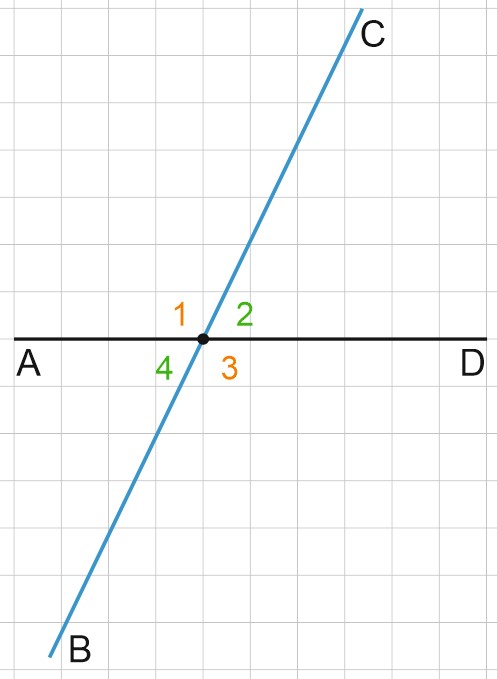
Здесь, как и на предыдущем чертеже, мы видим развернутые, острые и тупые углы.

И еще мы видим четыре пары смежных углов:

\(\angle 1+\angle 2=180^{\circ};\)

\(\angle 2+\angle 3=180^{\circ};\)

\(\angle 3+\angle 4=180^{\circ};\)

\(\angle 4+\angle 1=180^{\circ}.\)

А еще здесь есть равные углы.

\(\angle 1=\angle 3\) (обозначены оранжевым),

\(\angle 2=\angle 4\) (обозначены зеленым).

Такие углы называют вертикальными. Вертикальные углы равны.

\(\angle 1=\angle 3;\)

\(\angle 2=\angle 4.\)

Это легко доказать, используя смежные углы.

Например,

\(\angle 1+\angle 2=180^{\circ};\)

\(\angle 2+\angle 3=180^{\circ}.\)

Вычитая из второго равенства первое, получим, что \(\angle 1=\angle 3.\)

Определение: Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

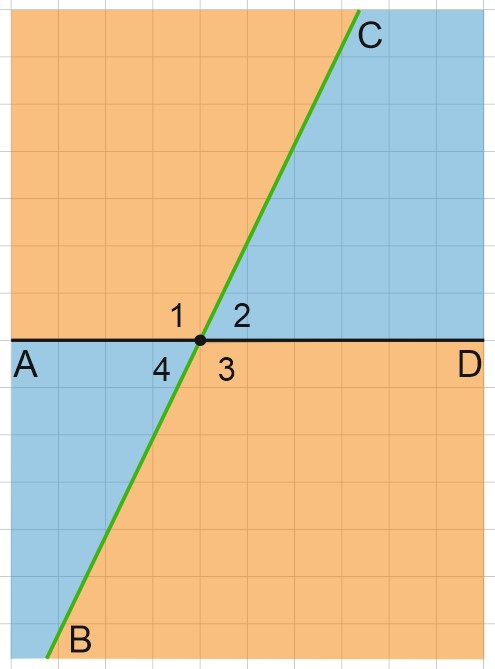
Вертикальные углы равны.

Положим два карандаша параллельно, а третий будет их пересекать. Получим новый чертеж.

Напомним, что параллельные прямые – это прямые, которые никогда не пересекаются. Обозначается это так: \(a \parallel b\). А новая прямая \(c\) называется секущая.