Линейная функция

Линейная функция – это функция вида \(y = kx+b\). Ее график – прямая линия.
Вспомним, что такое функция.

Функция - это зависимость одной переменной от другой по определенному закону или правилу.

Возьмем пример из жизни. У Маши есть кот Барсик, который каждый день съедает \(2\) пакетика кошачьего корма. Конечно, у Барсика и другие замечательные способности, и о нем можно написать целый рассказ. Но математики в своих задачах все упрощают, строят, как говорят, математические модели. Какого цвета Барсик, какие у него привычки, - для решения задачи неважно, и об этом не говорится. Важно то, что он ест \(2\) пакетика корма в день.

Если Маша покупает Барсику корм на \(2\) дня, ей надо купить \(4\) пакетика.

На \(3\) дня – \(6\) пакетиков.

На \(x\) дней Барсику нужно \(2x\) пакетиков корма.

Зависимость \(y= 2x\) – это пример функции. Ее можно назвать прямой пропорциональностью. Чем больше дней, тем больше пакетиков корма для Барсика.

Еще раз повторим определение:

Функция - это зависимость одной переменной от другой по определенному закону или правилу. 

В нашем примере количество купленных пакетиков корма зависит от количества дней.

Другой пример: грузовик едет по шоссе с постоянной скоростью \(v\) из одного города в другой.

Расстояние, которое он проедет за время \(t\), выражается формулой: \(S=vt\). Такое движение в физике называется равномерным. Чем больше время, тем больше расстояние. Расстояние зависит от времени. Можно сказать, что здесь расстояние - функция от времени.

Мы начнем с таких функций, как в наших примерах. \(y = 2x\) или \(S = vt\) – это линейные функции.

Зависимость, которую они выражают, - это прямая пропорциональность. Чем больше одна величина, тем больше другая.

Для построения графика линейной функции достаточно двух точек – потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.

Угловой коэффициент прямой

Величина \(k\) в формуле линейной функции \(y = kx+b\) называется угловым коэффициентом прямой. Он отвечает за угол наклона прямой.

Если \(k > 0\), линейная функция возрастает. Чем больше \(x\), тем больше \(y\), и график идет вправо и вверх.

Если \(k < 0\), линейная функция убывает. Чем больше \(x\), тем меньше \(y\), и график идет вправо и вниз.

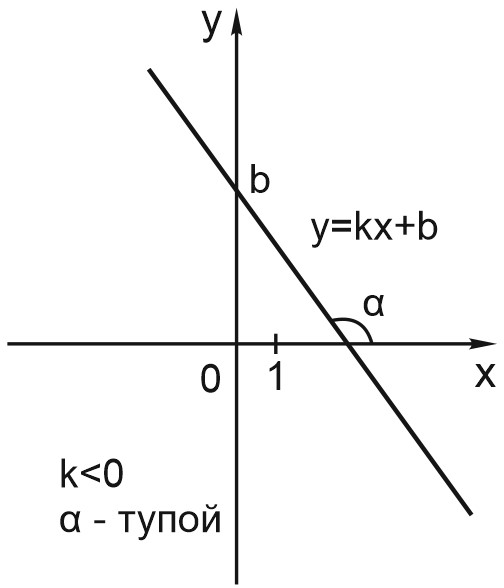
Пусть \(k > 0\). Чем больше \(k\), тем круче вверх идет график функции.

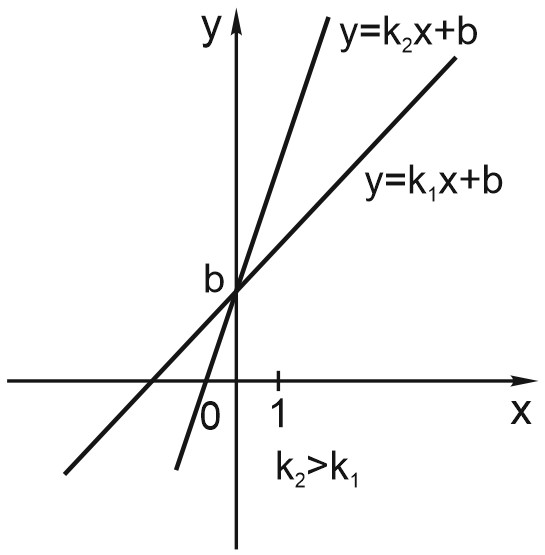
А число \(b\) в формуле отвечает за точку пересечения графика с осью ординат, то есть с вертикальной осью \(Y\).

Например, прямая \(y = 7x + 4\) пересекает ось \(Y\) в точке \((0; 4)\).

Прямая \(y =x -2\)  пересекает ось ординат в точке \((0; -2)\). Прямая \(y= 3x+ 10\) пересекает ось ординат в точке \((0; 10)\).

Можно сказать, что \(b\) – это значение линейной функции при \(x= 0\).

Рассмотрим частные случаи:

1. Если \(k = 0\), то \(y=b\), прямая параллельна оси абсцисс (оси \(X\)):

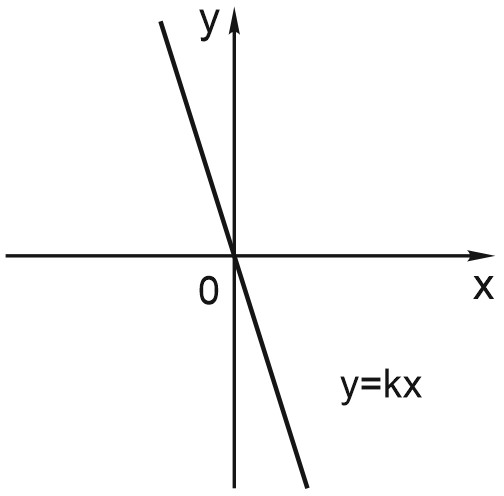
2. Если \(b = 0\), то \(y=kx\) (такая функция называется прямой пропорциональностью).

Ее график проходит через начало координат:

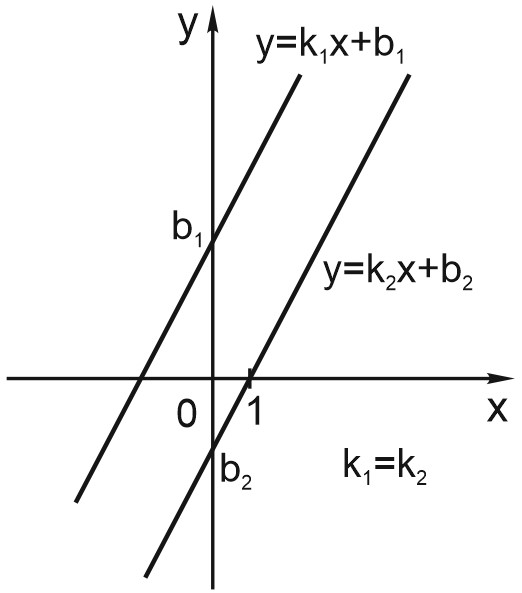
3. Если для двух прямых \(k_1=k_2\), прямые параллельны.

При этом, чем больше \(b\), тем выше расположен на координатной плоскости график функции.

Например, прямые \(y= 4 x + 3\) и \(y= 4x + 9\) параллельны. Их угловые коэффициенты равны.

Перечислим свойства линейной функции \(y= kx+b\):

1. Область определения функции – от минус бесконечности до плюс бесконечности. Это значит, что любое х можно подставить в формулу функции \(y= kx+b\).

Напомним, что область определения функции - это множество всех значений \(x\), для которых функция определена. Другими словами, те \(x\), которые можно подставить в формулу.

2. Область значений функции – тоже от минус бесконечности до плюс бесконечности.

Область значений - это те значения, которые может принимать \(y\).

3.  Линейная функция не имеет ни наибольшего, ни наименьшего значений.

4.  График функции пересекает ось \(OX\) в точке \(\left(\displaystyle -\frac{b}{k}; 0\right)\), ось \(OY\) – в точке \((0; b )\).

Разберем задачи на линейную функцию из ОГЭ по математике.

1. На рисунке изображен график функции вида \(y= kx+b\). Установите соответствие между графиками функции и знаками коэффициентов \(k\) и \(b\).

Графики

Коэффициенты

1)\(k < 0, \; b > 0;\)

2) \(k > 0, \; b > 0;\)

3) \(k < 0, \; b < 0;\)

4) \(k > 0, \; b < 0\).

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б	В
		f

 
Решение:

А) Видим, что функция возрастает, значит, \(k > 0\).

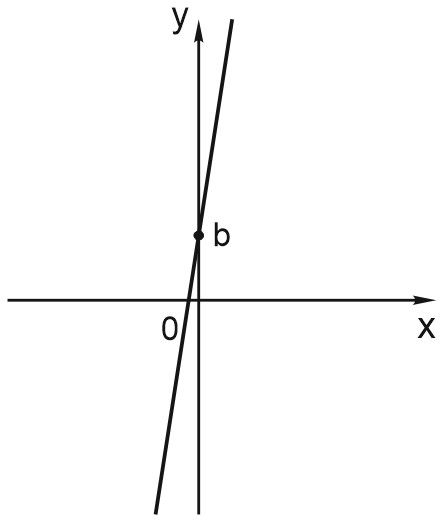
Точка пересечения графика функции с осью \(OY\) расположена выше нуля, поэтому \(b > 0\). Из предложенных вариантов подходит номер 2.

Б)

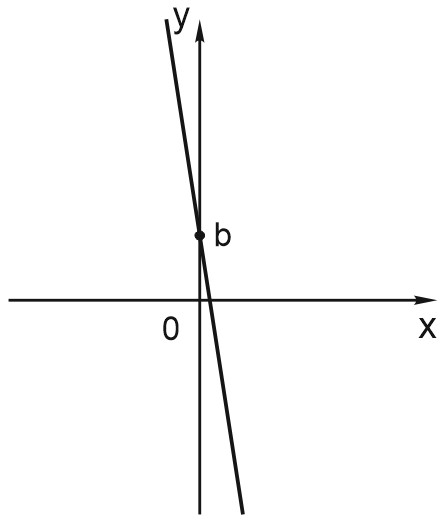
Функция убывает, значит, \(k < 0\). Точка пересечения \(OY\) находится выше нуля, следовательно, \(b > 0\). Подходит вариант 1.

В)

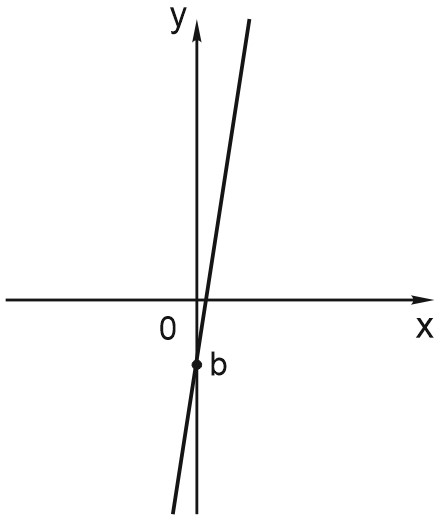
Функция возрастает, \(k > 0\).

Точка пересечения графика с осью \(OY\) ниже нуля, а значит, \(b < 0\).

Выбираем вариант 4.

В этом задании ответ: 214

2.  Установите соответствие между функциями и их графиками.

Функции

А) \(y=-2x+4\);

Б) \(y=2x-4\);

В) \(y=2x+4\).

Графики

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

 

 

Решение:

А) \(y=-2x+4\).

\(k=-2 < 0\), следовательно, функция убывает. \(b=4\), точка пересечения прямой с осью \(OY\) выше нуля.  Подходит вариант под цифрой 4.

Б) \(y=2x-4\).

\(k=2 > 0\), следовательно, функция возрастает.

\(b=-4\), значит, точка пересечения прямой с осью \(OY\) ниже нуля.

Подходит график под номером 3.

В) \(y=2x+4\).

\(k=2 > 0\), функция возрастает.

\(b=4\), точка пересечения прямой с осью \(OY\) выше нуля.

Подходит график под номером 2.

В ответе запишем набор цифр: 432

3. Установите соответствие между графиками функций и формулами, которые их задают.

Графики

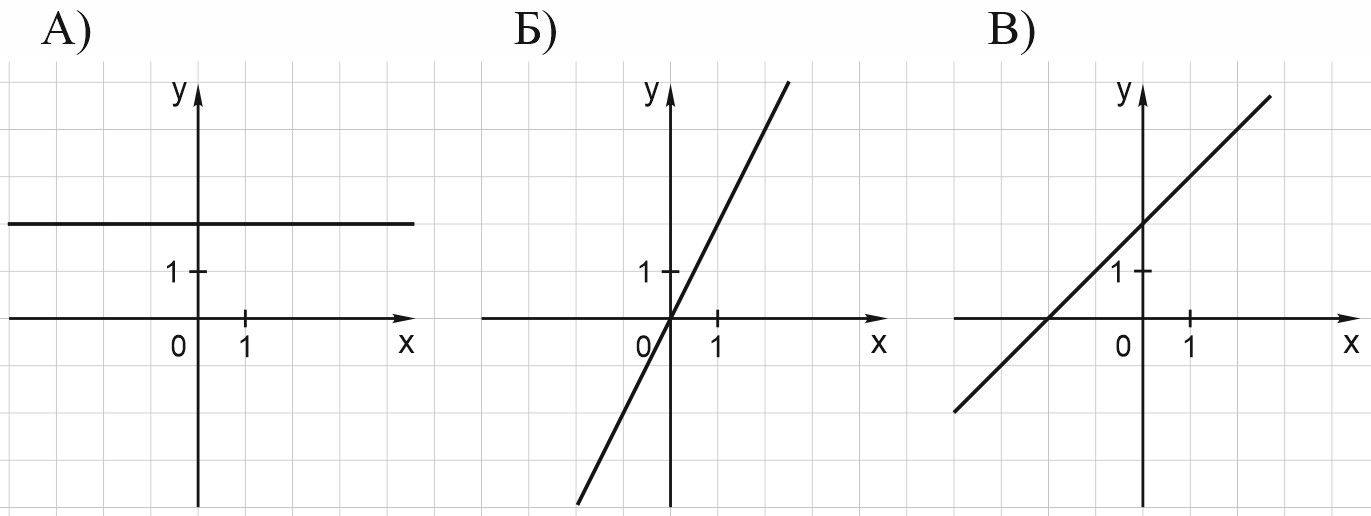
Формулы

1) \(y=2x\);  

2) \(y=-2x\);

3) \(y=x+2\);

4) \(y=2\).

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

 
Решение:

А) Прямая параллельна оси абсцисс и проходит через точку \((0; 2)\), значит, это функция \(y=2\). Вариант под номером 4.

Б) Прямая проходит через начало координат – подходят здесь два варианта: 1 и 2. Но функция на рисунке возрастает, для нее \(k > 0\), выбираем вариант 1.

В) Функция возрастает, и точка пересечения графика с осью \(OY\) находится выше нуля. Подходит единственный вариант 3.

В ответе пишем набор цифр: 413

4. Найти координаты точки пересечения графиков функций \(y_1=2x-5\)  и \(y_2=x+3\).

Решение:

Можно построить два графика и увидеть координаты точки пересечения на координатной плоскости. Это графический метод.

Есть второй способ. Он называется аналитический. Если мы решаем этим способом, можно ничего не рисовать. Мы просто решаем уравнения.

Точка пересечения лежит и на одной, и на другой прямой. Значит, ее координаты можно подставить в формулы для обеих функций и получить верные равенства.

Чтобы найти абсциссу точки пересечения графиков, мы просто приравниваем правые части в формулах функций:

\(2x-5=x+3\).

И решаем линейное уравнение:

\(2x-x=3+5\).

\(x=8\), подставив это значение в формулу любой из функций, получаем:

\(y=2\cdot 8-5=16-5=11\).

Ответ: \((8; 11)\)

5. Найти точки пересечения графика функции \(y=0,5x+3\)  с осями координат.

Решение:

1) Точка пересечения с осью \(OX\): \(y=0\).

\(0,5x+3=0\);

\(0,5x=-3\);

\(x=-3:0,5\);

\(x=-6\).

Точка пересечения с осью \(OX\) имеет координаты \((-6; 0)\).

2) Точка пересечения с осью \(OY\): \(x=0\).

\(y=0,5\cdot 0+3=3\).

Точка пересечения с осью \(OY\) имеет координаты \((0; 3)\).

6. Проходит ли график функции \(y=-4x-1\) через точки \((3;-13)\) и \((-5;-4)\)?

Решение:

Подставим по очереди координаты каждой из точек в уравнение прямой и проверим, верно ли равенство:

1) \(x=3, y=-13\).

\(-13=-4\cdot 3-1\);

\(-13=-13.\)

Равенство верно, следовательно, прямая проходит через точку или, другими словами, точка принадлежит графику функции.

2) Проверим вторую точку. Ее координаты \(x=-5, y=-4.\)

\(-4=-4\cdot (-5)-1\);

\(-4=19\),  неверно, значит, прямая через вторую точку не проходит.