Линейные уравнения

Вспомним, что такое уравнение.

Уравнение – это равенство, содержащее неизвестную переменную.

Например, \(2x = 4\) – уравнение.

Корень уравнения – значение переменной, при котором уравнение превращается в верное равенство. Число \(2\) является корнем уравнения \(2x=4\). Подставив \(2\) вместо \(x\), мы получим, что \(4= 4\).

Решить уравнение – значит найти все его корни или доказать, что корней нет.

Равносильными называют уравнения, множества решений которых совпадают.

Два уравнения равносильны, если все решения первого уравнения являются решениями второго и все решения второго являются решениями первого. У них одни и те же решения.  Уравнения, не имеющие корней, также считают равносильными.

Например, уравнения \(2x = 4\) и \(x= 2\) равносильны. Число \(2\) является корнем и одного, и другого уравнения, и других корней у них нет.

Записывается это так: \(2x=4\Leftrightarrow x=2.\)

У нас появился новый символ: \(\Leftrightarrow \) (читается: равносильно).

Стрелочки и в ту, и в другую сторону. Это значит, что если \(2x = 4\), то \(x = 2\). А если \(x=2\), то \(2x=4\).

Линейные уравнения

Линейное уравнение с одной переменной - это вот такое уравнение: \(ax = b\). Здесь \(x\) – переменная, \(a\) и \(b\) – числа.

Уравнение \(2x=4\) – линейное с одной переменной.

Правила решения линейных уравнений:

\(1)\) Можем перенести любое слагаемое из одной части в другую с противоположным знаком.

\(2)\) Можем умножать или делить обе части уравнения на одно и то же число, не равное нулю.

При этом мы получаем уравнение, равносильное исходному.

Пример 1. Решите уравнение: \(3(x-1)-2(3x+4)=1\).

Решение:

Раскроем скобки в левой части уравнения: \(3x-3-6x-8=1\).

Приведем подобные слагаемые в левой части.

Если из \(3x\) вычесть \(6x\), получится \(-3x\). Если из \(-3\) вычесть \(8\), получится \(-11\).

Теперь уравнение выглядит так: \(-3x-11=1\).

Перенесем слагаемое \(-11\) в правую часть с другим знаком, то есть с «плюсом»:

\(-3x=1+11\).

Получим: \(-3x=12\).

Отсюда \(x=-4\).

Наше уравнение имеет один корень.

Ответ: -4.

Пример 2. Решите уравнение: \(\displaystyle \frac{3x-1}{6}-\frac{x}{3}=\frac{5+x}{9}\).

Решение:

Умножим обе части уравнения на общий знаменатель всех дробей. Общий знаменатель равен \(18\). Получим: \(18\cdot \displaystyle \frac{3x-1}{6}-18\cdot \frac{x}{3}=18\cdot \frac{5+x}{9}\).

Сократив дроби, получим: \(3(3x-1)-6x=2(5+x)\).

Раскроем скобки: \(9x-3-6x=10+2x\).

Перенесем все слагаемые с переменной \(x\) в левую часть, остальные – в правую:

\(9x-6x-2x=3+10\).

Отсюда: \(x=13\).

Ответ: 13.

Пример 3. Решите уравнение: \((4x+1)(2x-4)-8x^2=3(6-x)\).

Решение:

Раскроем скобки: \(8x^2-16x+2x-4-8x^2=18-3x\).

После переноса слагаемых и приведения подобных получим уравнение:

\(-11x=22\).

Отсюда \(x=-2\).

Ответ: -2

Полезная информация для отличников

Как вы считаете - всегда ли линейное уравнение имеет решение?

Мы помним, что линейное уравнение с одной переменной имеет вид: \(ax=b\).

Число \(a\) называют коэффициентом при переменной, \(a\) число \(b\) – свободным членом.

Оказывается, при решении линейного уравнения \(ax=b\) возможны 3 случая:

\(1)\) Если \(a\neq0\), \(b\) – любое число, то уравнение имеет ровно один корень \(x=-\displaystyle \frac{b}{a}\).

Например, уравнение \(5\cdot x=15\) имеет единственный корень \(x=3\).

\(2)\) Если \(a=0\), \(b=0\), то уравнение принимает вид \(0\cdot x=0\). Это равенство верно при любом \(x\), поэтому корнем уравнения будет любое число.

\(3)\) Если \(a=0\), \(b\neq0\), то уравнение принимает вид \(0\cdot x=b\). При любом значении \(x\) в правой части уравнения получается ноль, а в левой части – не ноль.

В этом случае уравнение не имеет корней. Например, уравнение \(0\cdot x=4\) не имеет корней.

Текстовые задачи, сводящиеся к линейным уравнениям.

Часто в математике встречаются задачи, где в условии дан текст. Они похожи на короткие рассказы. Автобус и грузовик едут из одного города в другой. Велосипедист обгоняет пешехода. Две бригады строят дом. Такие задачи обычно решаются с помощью уравнений.

Вот как мы действуем:

\(1)\) Выбираем неизвестную величину и обозначаем ее переменной, например, \(x\). Часто за переменную обозначают величину, которую надо найти в задаче.

\(2)\) Можно сделать рисунок.

\(3)\) Выражаем другие неизвестные величины (если они есть) через эту переменную.

\(4)\) Вносим данные в таблицу.

\(5)\) Составляем уравнение согласно условию задачи.

\(6)\) Решаем уравнение.

\(7)\) Проверяем ответ с точки зрения здравого смысла. Например, если скорость пешехода оказалась равной \(300\) км/час, значит, задача решена неправильно.

\(8)\) Если все правильно, записываем ответ.

Посмотрим, как решать текстовые задачи с помощью линейных уравнений.

Пример 4. Расстояние от поселка A до поселка Б автобус проходит за \(5\) часов, а автомобиль – за \(3\) часа. Чему равно расстояние между поселками, если скорость автомобиля на \(30\) км/ч больше скорости автобуса? Ответ выразите в километрах.

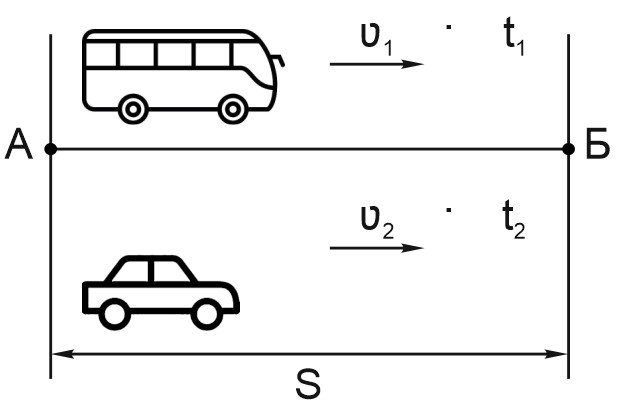
Решение:

Обозначим скорость автобуса за \(x\) км/ч, тогда скорость автомобиля \((x+30)\) км/ч.

Воспользуемся формулой \(S=V\cdot t\) (\(S\) -  расстояние, \(V\) – скорость, \(t\) – время).

Тогда расстояние, которое проехал автобус, равно \(5x\) км.

Расстояние, которое проехал автомобиль, равно \(3(x+30)\) км. По условию задачи, это одно и то же расстояние.

Составим и решим уравнение: \(5x=3(x+30)\).

Отсюда: \(2x=90\),

\(x=45\). Значит, скорость автобуса равна \(45\) км/ч.

Расстояние, которое он проехал, равно \(45\cdot 5=225\) км.

Ответ: 225.

Пример 5. Соседи Кирилл и Федор переносят кирпичи с одного дачного участка на другой в течение одного часа. Кирилл переносит в минуту на \(1\) кирпич меньше, чем Федор. Всего они перенесли \(300\) кирпичей. Сколько кирпичей переносит в одну минуту Федор?

Решение:

Обозначим за \(x\) количество кирпичей, которые Федор переносит в минуту. Тогда Кирилл переносит \((x-1)\) кирпичей. Вместе в минуту они переносят \(x+x-1= 2x-1\) кирпичей. А за \(1\) час, который равен \(60\) минутам, они перенесут \(60\cdot (2x-1)\)  кирпичей. По условию, это \(300\) кирпичей. Составим уравнение: \(60(2x-1)=300\).

Решая его, найдем \(x=3\). Значит, Федор переносит в минуту \(3\) кирпича.

Ответ: 3.

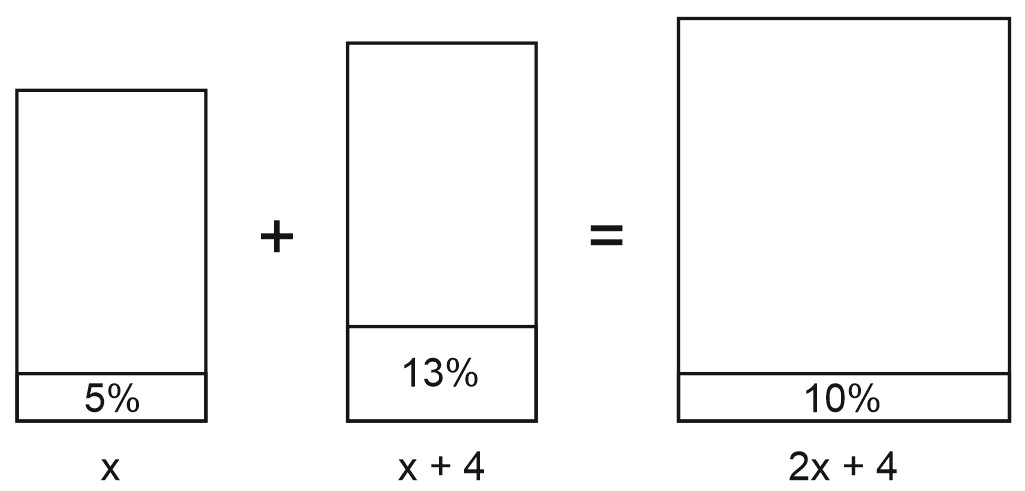
Пример 6 (повторение). Первый сплав содержит \(5\)% меди, второй — \(13\)% меди. Масса второго сплава больше массы первого на \(4\) кг. Из этих двух сплавов получили третий сплав, содержащий \(10\)% меди. Найдите массу третьего сплава.

Решение:

Такие задачи мы решали в теме "Сплавы, смеси, растворы".

Обозначим массу первого сплава \(x\) кг.

Тогда масса второго сплава \((x+4)\) кг, а третьего \(x+x+4=2x+4\) кг.

Для удобства переведем проценты в дроби:

\(5\)% \(=0,05\);

\(13\)% \(=0,13\);

\(10\)% \(= 0,1\).

Тогда по условию задачи в первом сплаве содержится \(0,05x\) кг меди, во втором  — \(0,13(x+4)\) кг, в третьем сплаве содержится \(0,1(2x+4)\) кг меди.

Составим и решим уравнение:

\(0,05x+0,13(x+4)=0,1(2x+4)\).

Домножим обе части уравнения на \(10\), чтобы коэффициенты стали целыми.

\(5x+13(x+4)=10(2x+4)\).

После преобразований получим равносильное уравнение \(2x=12\).

Отсюда находим \(x=6\).

Значит, масса первого сплава равна \(6\) кг, тогда масса второго сплава равна \(10\)  кг, а масса третьего сплава \(16\) кг.

Ответ: 16.