Подобные треугольники. Признаки подобия треугольников

Подобные треугольники

В курсе геометрии нам встречаются не только равные, но и подобные треугольники. Разберемся, что такое подобные фигуры.

На рисунке два котика.

Их форма одинакова, пропорции одинаковы. И отличаются они только размерами. Такие фигуры называются подобными.

Коэффициент подобия показывает, во сколько раз размеры одной из подобных фигур больше размеров другой.

Во сколько раз высота первого котика больше высоты второго. Во сколько раз хвостик у первого длиннее, чем у второго.

В геометрии мы обычно говорим о подобных треугольниках. Вот они:

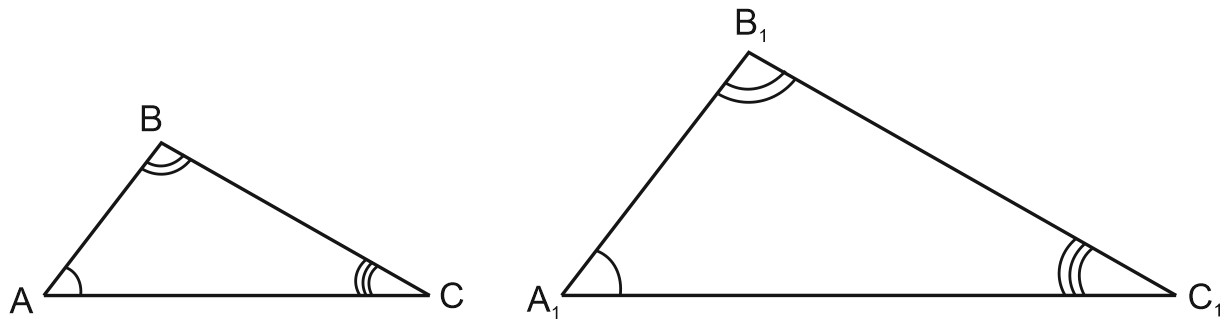
Про них можно сказать, что форма у них одинаковая, а размеры разные.

Обозначается это так: \(\triangle ABC \sim \triangle A_{1}B_{1}C_{1}.\)

Значок \( \sim\) обозначает «подобие».

Посмотрим внимательно на треугольники \(ABC\) и \(A_{1}B_{1}C_{1}.\)

У этих треугольников все углы попарно равны. Угол \(A\)  равен углу \(A_1\), угол \(B\)  – углу \(B_1\)  и угол \(C\)  – углу \(C_1\).

А стороны этих треугольников пропорциональны. Сторона \(B_1C_1\)  во столько же раз длиннее \(BC\) , во сколько раз \(A_1C_1\)  длиннее \(AC\).

Стороны подобных треугольников, лежащие напротив равных углов, называют сходственными.

\(\displaystyle \frac{A_1 B_1}{AB}=\frac{B_1 C_1}{BC}=\frac{A_1 C_1}{AC}=k.\)

Число \(k\) – это коэффициент подобия. Он показывает, во сколько раз у одного треугольника стороны больше, чем у другого.

Получается, что два треугольника подобны, когда три угла одного треугольника равны трем углам другого. И тогда выполняется соотношение:

\(\displaystyle \frac{A_1 B_1}{AB}=\frac{B_1 C_1}{BC}=\frac{A_1 C_1}{AC}=k.\)

Но оказывается, нам не обязательно проверять, чтобы все три угла одного треугольника были равны трем углам другого, и чтобы все стороны были пропорциональны. Можно обойтись меньшим количеством элементов.

Чтобы проверить, являются ли два треугольника подобными, мы применяем признаки подобия треугольников.

Признаки подобия треугольников

Первый признак подобия треугольников. По двум углам.

Два треугольника подобны, если два угла одного треугольника равны соответственно двум углам другого.

\(\angle A=\angle A_1, \; \angle B=\angle B_1\). Тогда \(\triangle ABC \sim \triangle A_{1}B_{1}C_{1}.\)

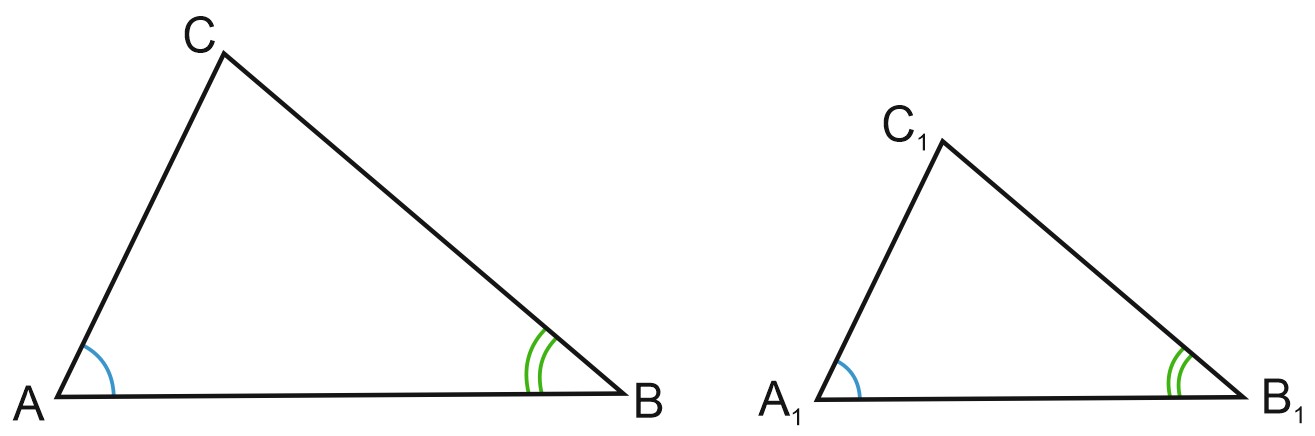
В самом деле, сумма углов треугольника равна \(180\) градусов. Зная два угла треугольника, мы легко находим третий. И если \(\angle A=\angle A_1\) и \(\angle B=\angle B_1\), то \(\angle C=\angle C_1\).

Второй признак подобия треугольников. По углу и двум прилежащим к нему сторонам.

\(\angle A=\angle A_1\) и \(\displaystyle \frac{AB}{A_1 B_1}=\frac{AC}{A_1 C_1}.\) Тогда \(\triangle ABC \sim \triangle A_{1}B_{1}C_{1}.\)

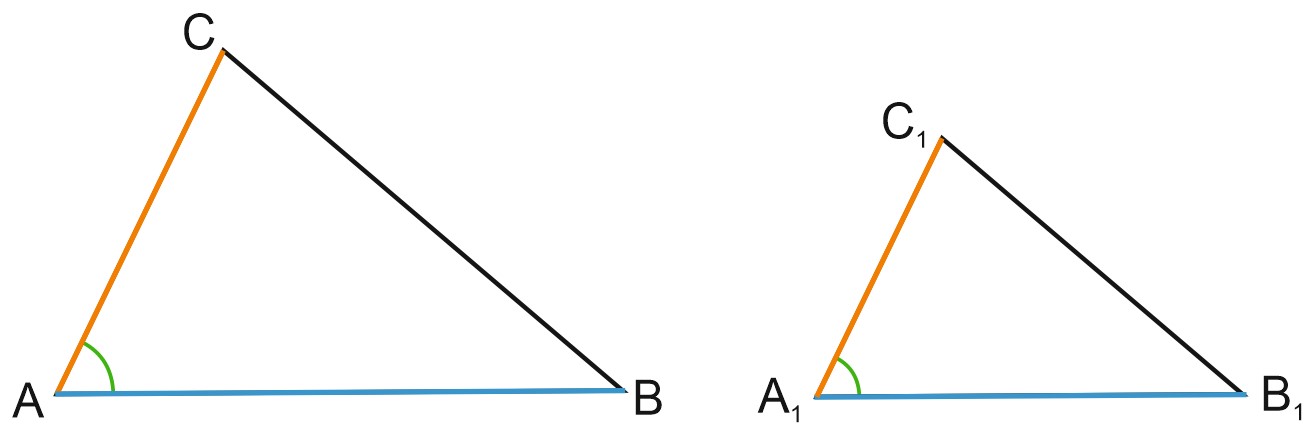
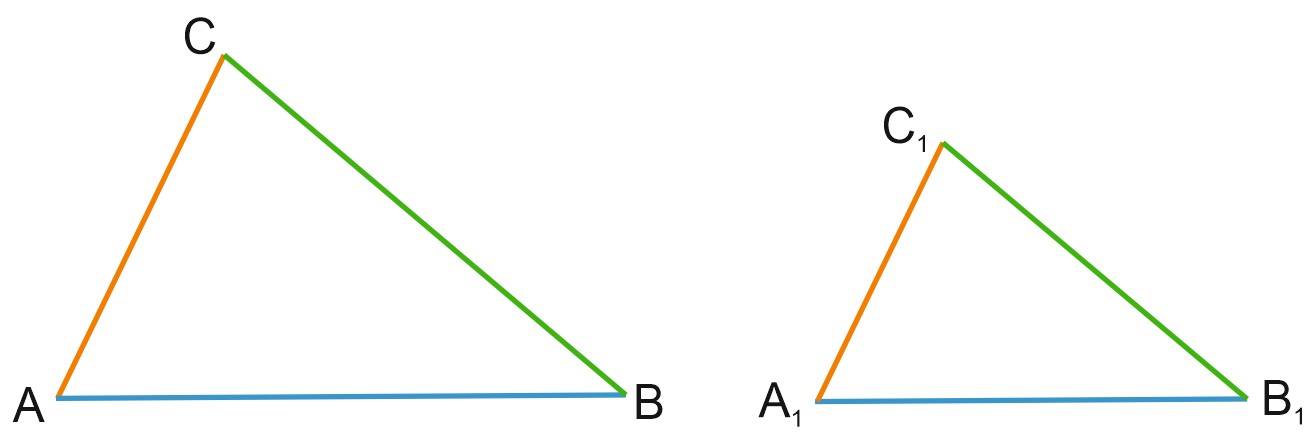
Третий признак подобия треугольников. По трем сторонам.

Два треугольника подобны, если все их стороны пропорциональны:

\(\displaystyle \frac{AB}{A_1 B_1}=\frac{BC}{B_1 C_1}=\frac{AC}{A_1 C_1}.\) Тогда \(\triangle ABC \sim \triangle A_{1}B_{1}C_{1}.\)

Запомним важное правило.

Отношение площадей подобных фигур равно квадрату коэффициента подобия.

На рисунке – подобные треугольники \(ABC\) и \(A_1 B_1 C_1\).

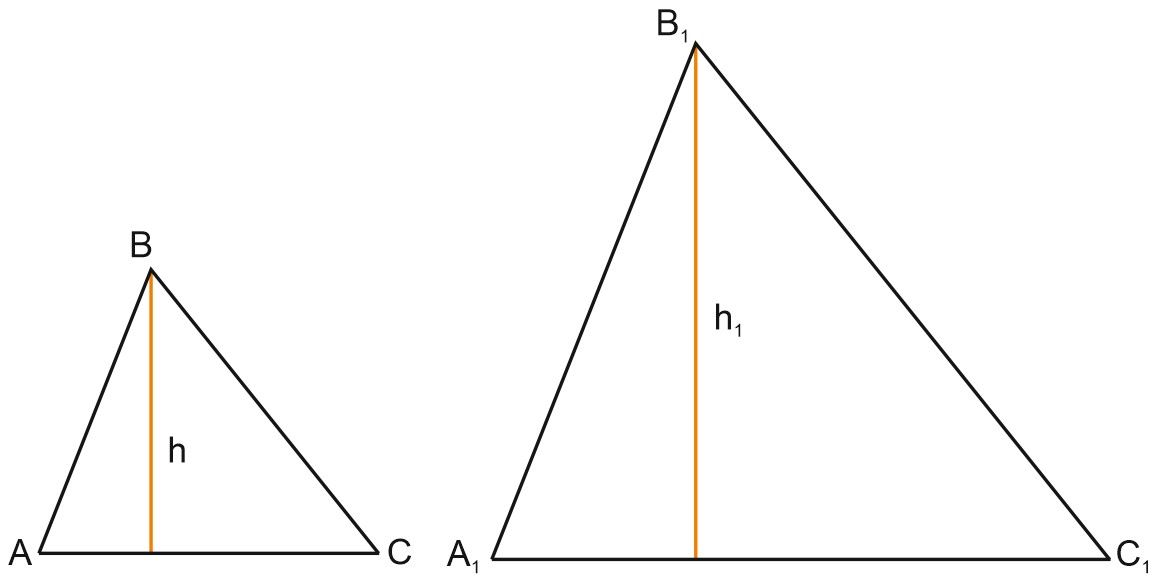
У треугольника \(A_1 B_1 C_1\) все стороны в \(k\) раз длиннее, чем у треугольника \(ABC\).

Высота треугольника \(A_1 B_1 C_1\) в \(k\) раз длиннее, чем высота треугольника \(ABC\).

Тогда площадь треугольника \(A_1 B_1 C_1\) в \(k^2\) раз больше, чем площадь треугольника \(ABC\).

Отношение площадей подобных фигур равно квадрату коэффициента подобия.

\( \displaystyle \frac{S_{\triangle A_{1}B_{1}C_{1}}}{S_{\triangle ABC}}=k^{2}\)

1. На одной стороне угла \(A\) отложены отрезки \(AB=6\) и \(AC=20\). На другой стороне \(AD=8\) и \(AE=15\).
Подобны ли треугольники \(ACD\) и \(AEB\)?

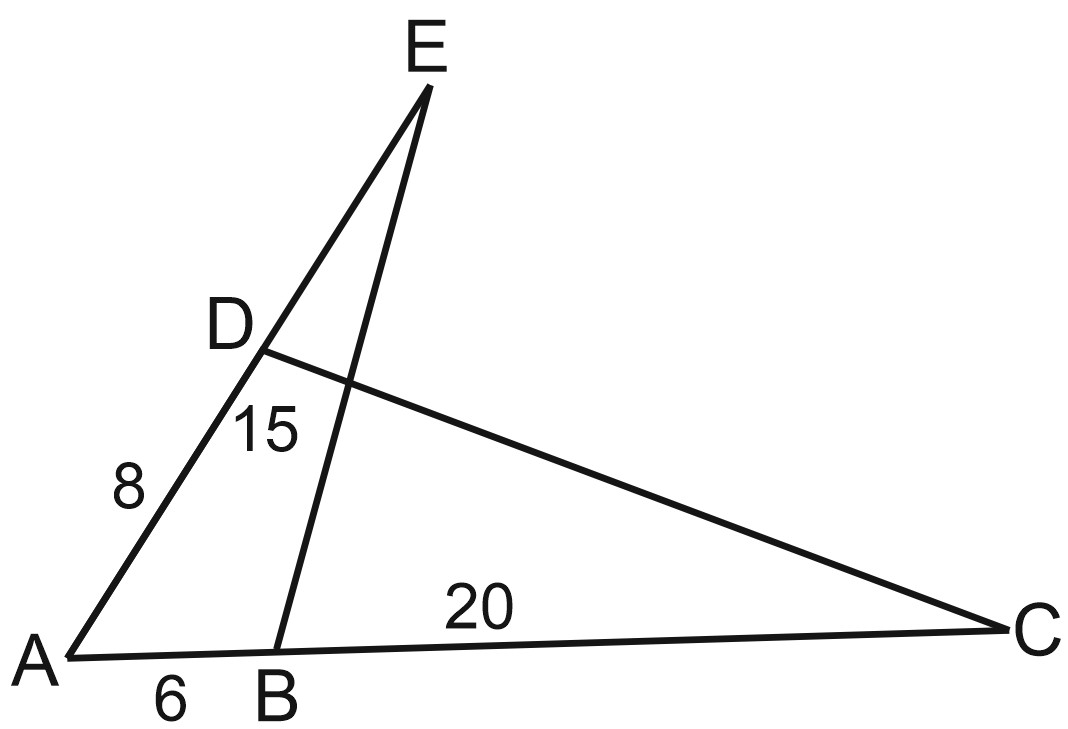
Решение:

Да, \(\triangle ACD\sim \triangle AEB\) по углу и двум прилежащим сторонам.

Угол \(A\) у них общий и лежит между пропорциональными сторонами:

\(\displaystyle \frac{6}{8}=\frac{15}{20}=\frac{3}{4}\).

Ответ: да.

2. Через точки \(M\) и \(N\), принадлежащие сторонам \(AB\) и \(BC\) треугольника \(ABC\) соответственно, проведена прямая \(MN\), параллельная стороне \(AC\). Найдите длину \(CN\), если \(BC=6, \; MN=4, \; AC=9.\)

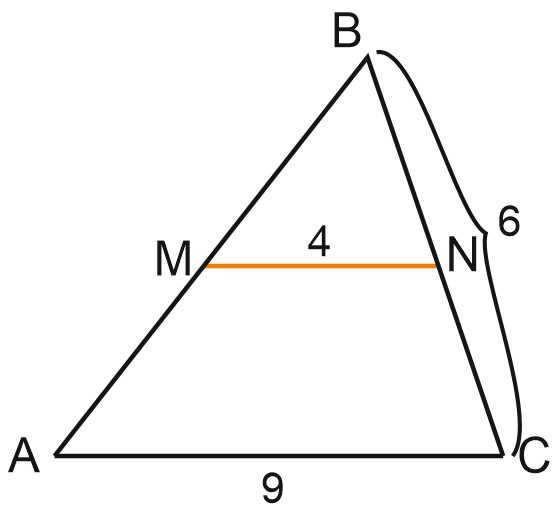
Решение:

1) У треугольников \(MBN\) и \(ABC\) угол \(B\) – общий.

2) Углы \(BMN\) и \(BAC\) равны, как соответственные при \(MN\parallel AC\) и секущей \(AB\).

Треугольники \(MBN\) и \(ABC\) подобны по двум сторонам.

Поэтому их стороны пропорциональны:

\(\displaystyle \frac{BN}{BC}=\frac{MN}{AC}=\frac{MB}{AB}.\)

Обозначим \(NC\) за \(x\), тогда \(BN=6-x.\)

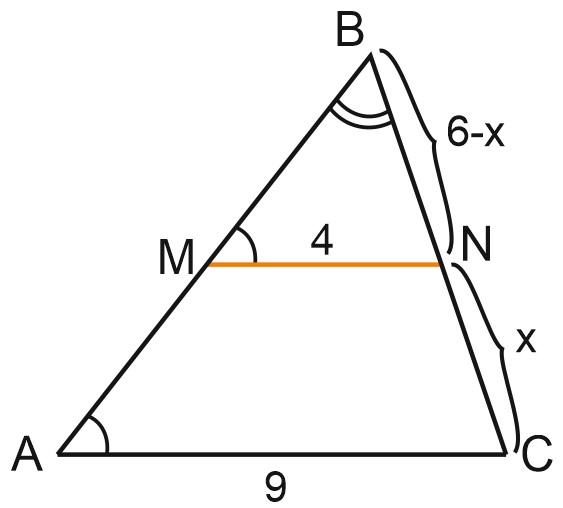
Запишем соотношение сходственных сторон:

\(\displaystyle \frac{6-x}{6}=\frac{4}{9};\)

\(9(6-x)=6\cdot 4;\)

\(x=\displaystyle \frac{10}{3}.\)

Ответ: \(\displaystyle \frac{10}{3}.\)

3. Пусть \(F\) – точка пересечения медиан \(AD\) и \(BE\) треугольника \(ABC\). Известно, что \(S_{ABF}=1\). Найдите \(S_{DEF}\).

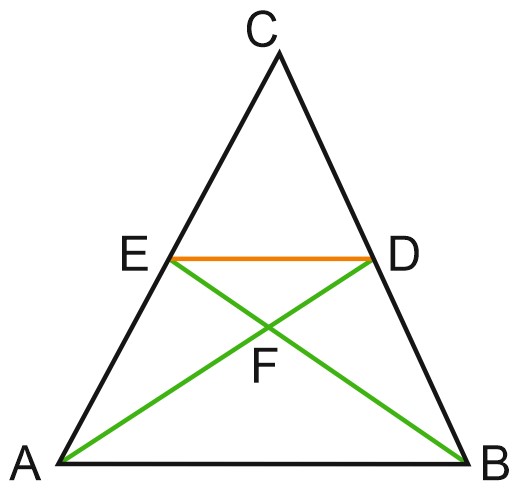
Решение:

Точки \(E\) и \(D\) – середины сторон \(AC\) и \(BC\) треугольника \(ABC\), тогда \(ED\) – средняя линия треугольника \(ABC\), \(ED \parallel AB\).

Так как \(ED\parallel AB\), то \(\angle DEF=\angle ABF, \; \angle EDF=\angle FAB\) (как внутренние накрест лежащие при параллельных прямых и секущей), следовательно, \(\triangle DEF\sim \triangle ABF\)  (по двум углам).

\(ED=\displaystyle \frac{1}{2} AB\), коэффициент подобия \(k=\displaystyle \frac{1}{2}\), поэтому \(\displaystyle \frac{S_{DEF}}{S_{ABF}}=\left (\displaystyle \frac{ED}{AB}\right)^2=0,5^2=0,25\).

Мы воспользовались тем, что отношение площадей подобных фигур равно квадрату коэффициента подобия.

По условию, \(S_{ABF}=1\), тогда \(S_{DEF}=0,25\).

Ответ: 0,25

4. Основания \(BC\)  и \(AD\)  трапеции \(ABCD\)  равны соответственно \(5\) и \(45\), \(BD=15\). Докажите, что треугольники \(CBD\)  и \(BDA\) подобны.

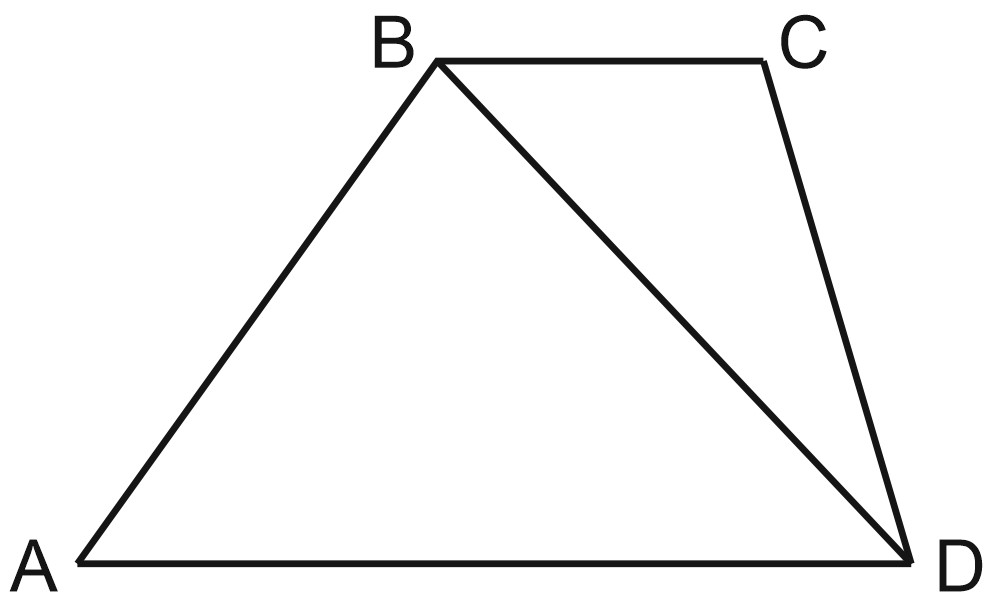
Решение:

Углы \(CBD\) и \(BDA\) равны, как накрест лежащие при \(BC\parallel AD\) и секущей \(BD\).

В треугольниках \(CBD\) и \(ADB\): \(\displaystyle \frac{BC}{BD}=\frac{BD}{AD}\).

Следовательно, эти треугольники подобны по двум сторонам и углу между ними.

5. Подобны ли треугольники, если их стороны равны:

1) 2, 3, 4 и 8, 12, 16;
2) 5, 7, 9 и 27, 15, 21;

Решение:

1) \(\displaystyle \frac{2}{8}=\frac{3}{12}=\frac{4}{16}=\frac{1}{4}.\)

Стороны треугольников относятся как \(1:4\), треугольники подобны.

2) \(\displaystyle \frac{5}{27}\neq\frac{7}{15}\neq\frac{9}{21}.\)

На первый взгляд, соотношение не выполняется. Но дело в том, что длины сторон треугольников могут быть даны не в том порядке. Для удобства расположим их в порядке возрастания: 5, 7, 9 и 15, 21, 27. Меньшая сторона одного треугольника должна быть пропорциональна меньшей стороне второго треугольника. Также пропорциональны и другие их стороны.

\(\displaystyle \frac{5}{15}=\frac{7}{21}=\frac{9}{27}=\frac{1}{3}\) – да, треугольники подобны.