Равные треугольники. Признаки равенства треугольников

На рисунке показаны два треугольника. С первого взгляда мы видим, что они одинаковые, то есть равные.

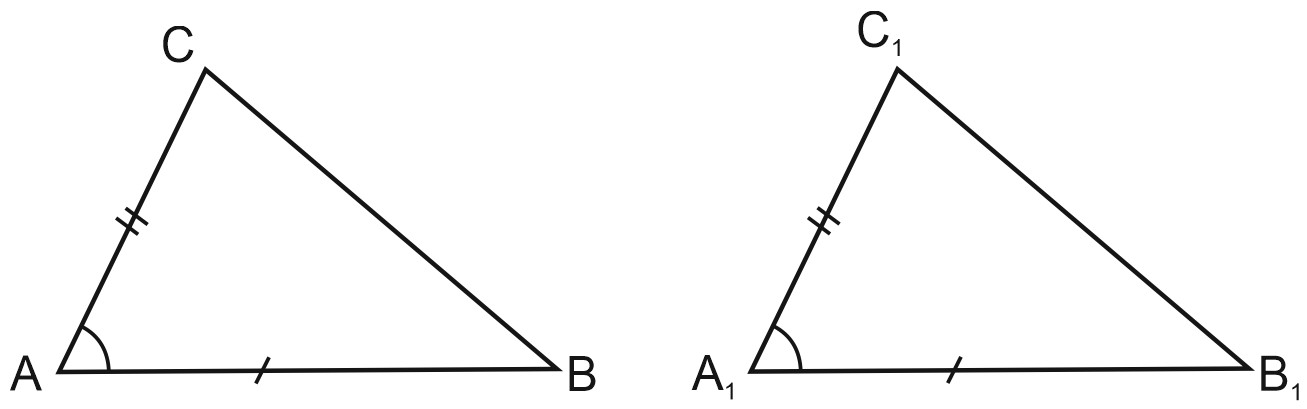
Если мы измерим линейкой их стороны, то увидим, что они равны:

\(AC=A_1C_1, \; BC=B_1C_1, \; AB=A_1B_1.\)

Измерив транспортиром их углы, убедимся, что напротив равных сторон лежат равные углы.

Представим себе, что мы вырезали один из треугольников из бумаги и наложили его на другой. Треугольники совпадут, значит, они равные.

Углы \(A\) и \(A_1\) – равные, \(B\) и \(B_1\) – тоже, а также \(C\) и \(C_1\).

Равные треугольники не обязательно должны быть одинаково расположены. На следующем рисунке треугольники расположены по-разному. Но они тоже равные, потому что три стороны одного треугольника равны трем сторонам другого. А три угла одного треугольника равны трем углам другого.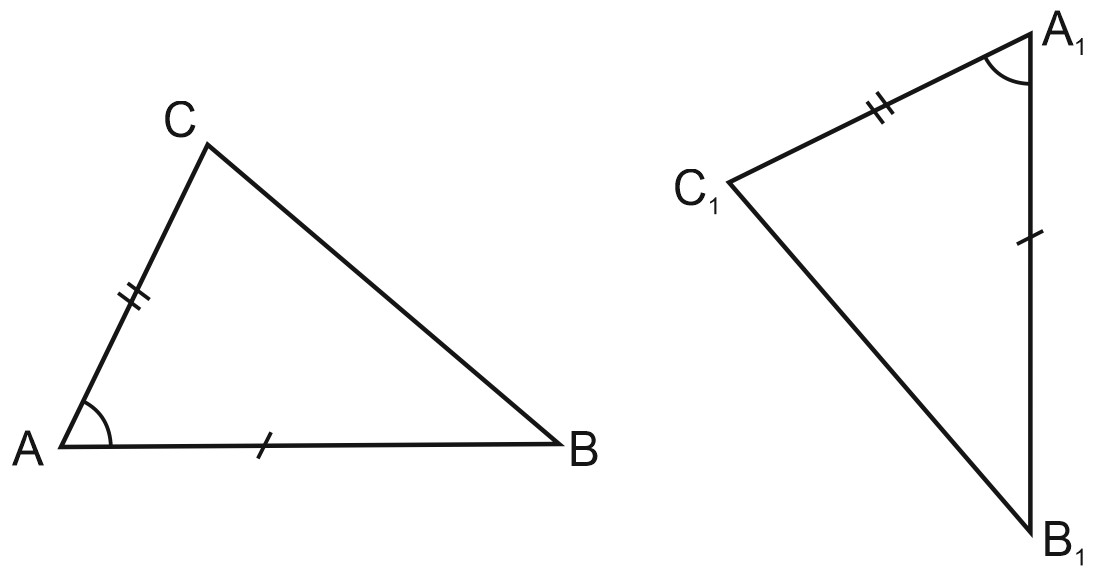 

Оказывается, что для равенства треугольников нам не обязательно проверять три стороны и три угла. Можно обойтись меньшим количеством сторон и углов.

Для того чтобы определить, равны треугольники или нет, мы используем признаки равенства треугольников. И в каждом случае мы берем не три угла и три стороны, а меньшее количество углов и сторон.

В геометрии применяют три признака равенства треугольников.

Первый признак равенства треугольников

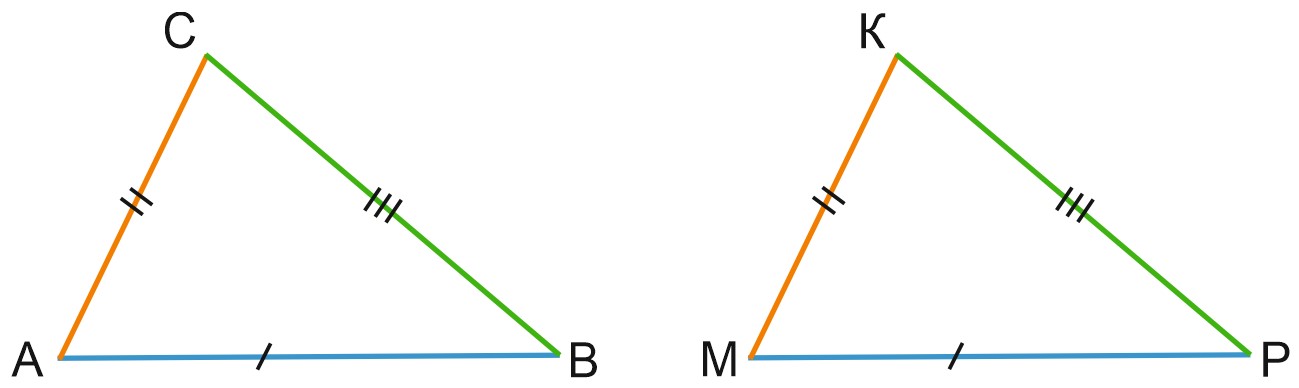
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.

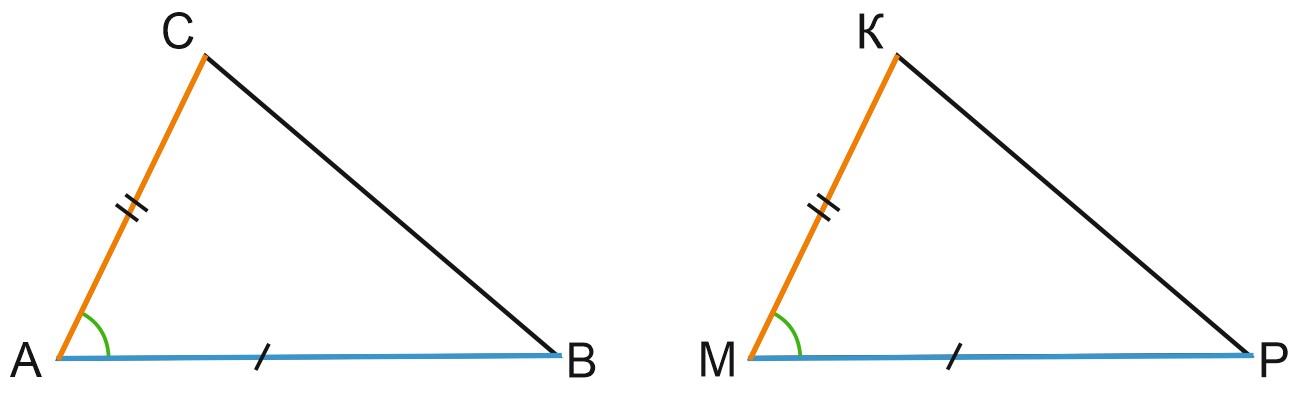
Треугольники \(ABC\) и \(MPK\) на рисунке равны, так как \(AC=MK, AB=MP, \) углы \(A\) и \(M\) – равны.

Зная две стороны и угол между ними, треугольник можно построить единственным образом.

Посмотрим, как это сделать. Возьмем отрезки \(a\) и \(b\) и угол \(C\).

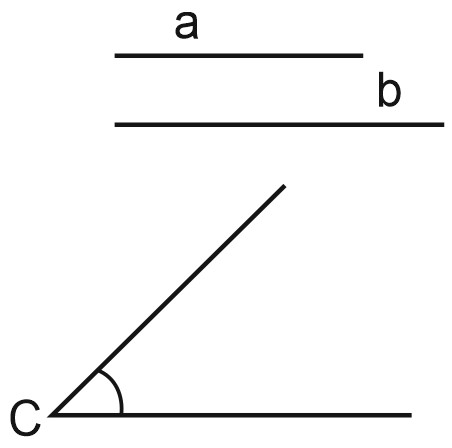
На сторонах угла \(C\) отметим отрезки \(BC\) и \(AC\) так, что \(BC=a, \; AC=b\). Отметить их можно с помощью циркуля. И соединим точки \(A\) и \(B\).

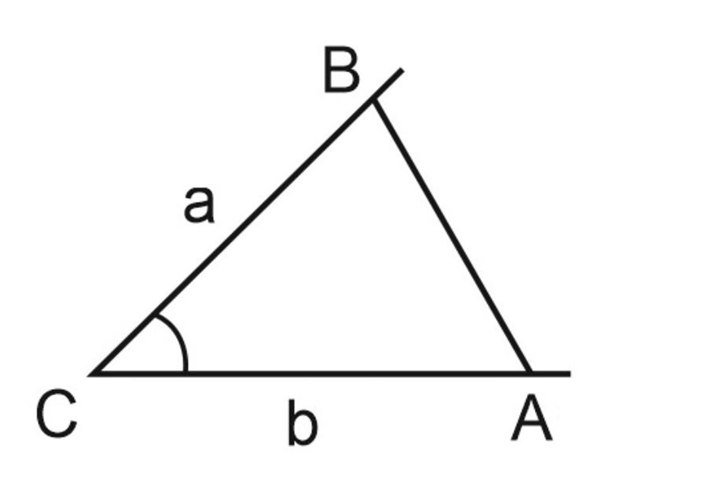
Мы получили треугольник, в котором \(AC=b, \; BC=a, \; \angle ACB=\angle C\).

Какими бы ни были отрезки \(a\) и \(b\) и угол \(C\), такой треугольник построить можно. При этом длина его третьей стороны и величины двух других углов определяются единственным образом.

Все треугольники, в которых соответственно равны две стороны и угол между ними, – равные.

Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.

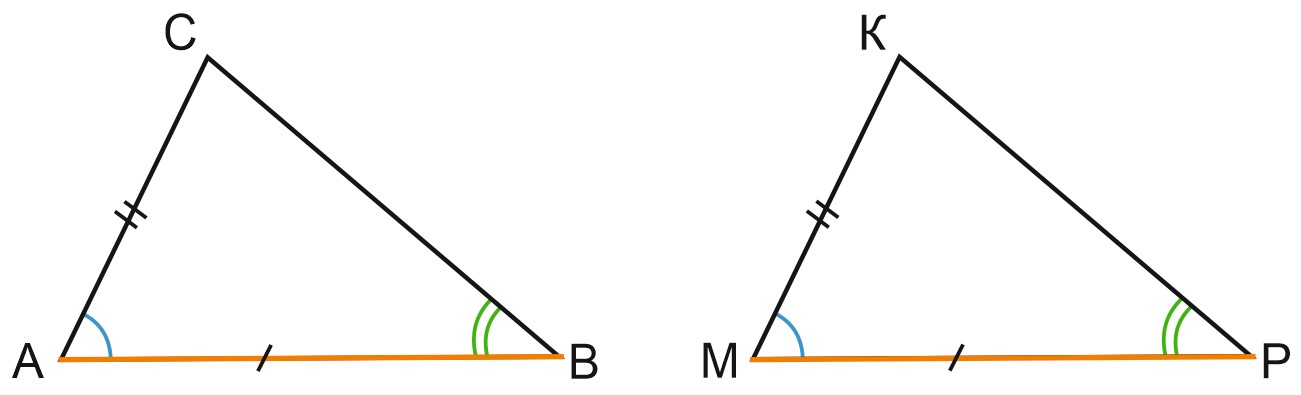
Это значит, что если нам даны сторона и два прилежащих к ней угла, то треугольник можно построить единственным образом.

Заметим, что сумма углов треугольника равна \(180^{\circ}\), поэтому треугольник можно построить, если сумма этих двух углов меньше \(180^{\circ}\).

Построим треугольник по стороне \(AB\) и двум прилежащим к ней углам \(A\) и \(B\). Возьмем отрезок \(AB\) длиной \(c\) и два угла, \(A\) и \(B\).

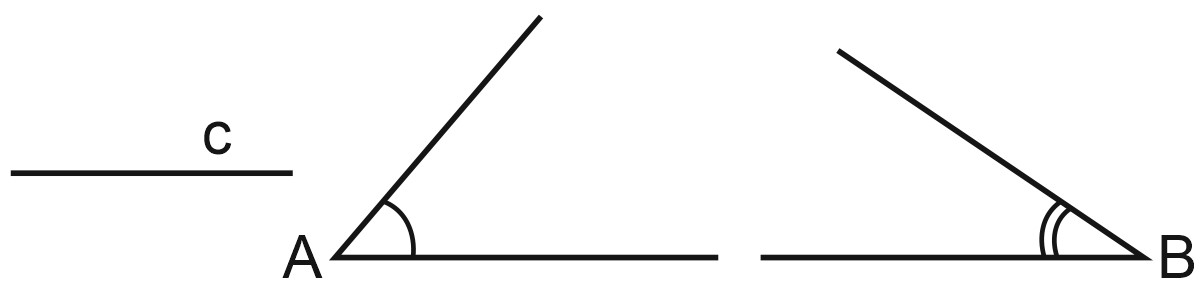
Можно сказать, что мы «пристраиваем» углы \(A\) и \(B\) с двух сторон к отрезку \(c\). Точка \(A\) будет вершиной угла \(A\), точка \(B\) – вершиной угла \(B\). И одна из сторон каждого угла лежит на отрезке \(c\).

Точку пересечения сторон построенных углов обозначим \(C\). Получился треугольник \(ABC\).

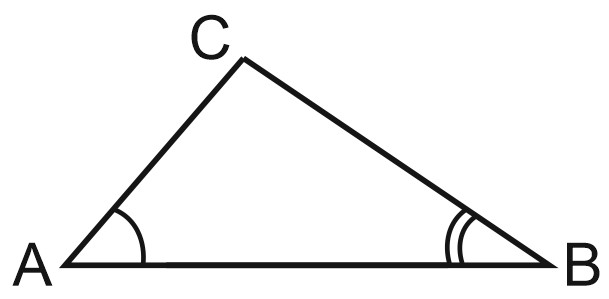
Значит, по стороне и двум прилежащим к ней углам треугольник можно построить единственным образом.

Точка \(C\) может быть расположена над отрезком \(AB\) или под ним – это неважно. Треугольники получаются равные.

Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трем сторонам другого, то треугольники равны.

Построим треугольник по трем сторонам.

Возьмем 3 отрезка, длины которых равны \(a, \; b\) и \(c\).

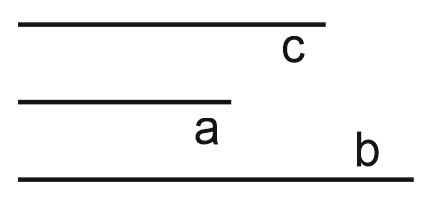
Отметим на концах отрезка \(b\) точки \(A\) и \(C\). И с помощью циркуля проведем окружность с центром в точке \(A\) и радиусом \(c\). Также с помощью циркуля проведем окружность с центром в точке \(C\) и радиусом \(a\).

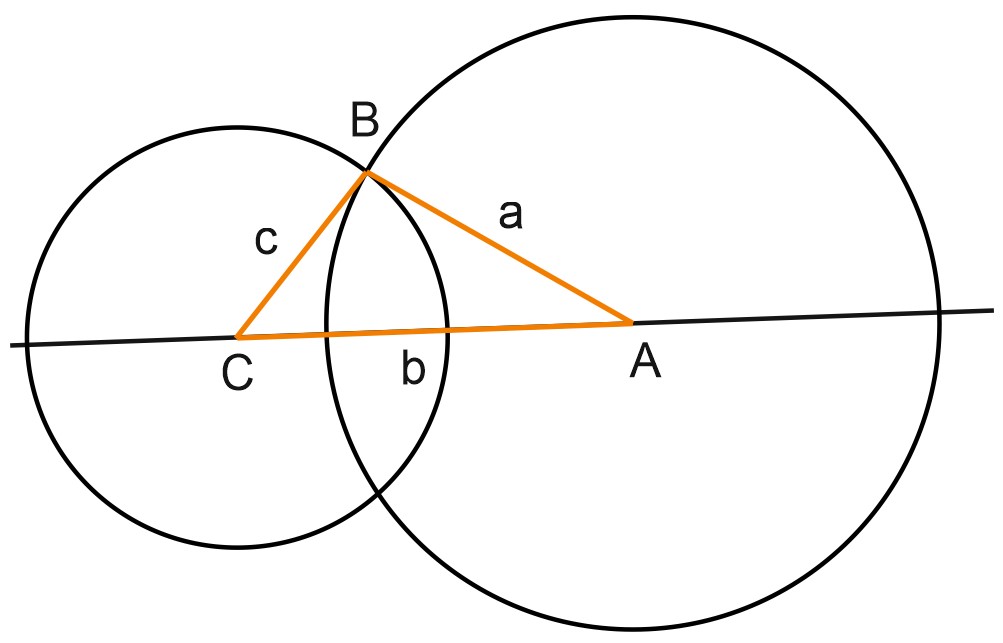
Окружности пересекаются в двух точках. Выберем любую из точек пересечения и обозначим ее буквой \(B\). Проведем отрезки \(AB\) и \(BC\). Получили треугольник \(ABC\).

Мы могли бы взять и нижнюю точку пересечения окружностей. Тогда получился бы треугольник, равный данному.

Значит, по трем сторонам треугольник можно построить единственным образом.

Зададим себе вопрос: всегда ли можно построить треугольник, длины сторон которого равны \(a, \; b\) и \(c\)? Не спешите с ответом. Посмотрите на наш рисунок. Мы сказали, что окружности пересекутся в двух точках. Но что, если радиусы окружностей с центрами в точках \(A\) и \(C\) такие маленькие, что их сумма меньше длины отрезка \(AC\)? – Тогда треугольника не получится.

Чтобы треугольник существовал, должно выполняться неравенство треугольника: сумма любых двух сторон треугольника больше третьей стороны.

Неравенство треугольника

\(AB + BC > AC;\)

\(AB + AC > BC;\)

\(AC + BC > AB.\)

Если хотя бы одно из этих неравенств не выполняется – треугольник не существует.

Например, треугольник со сторонами 2, 3 и 12 сантиметров существовать не может. Третья сторона оказалась больше суммы двух других.

Помните, как это объясняли в школе в 7 классе? Красная Шапочка выходит из точки \(A\) и идет к бабушке в точку \(C\). Если она по дороге зайдет к волку (в точку \(B\)), то расстояние будет больше, чем если она пойдет к бабушке по прямой. Потому что кратчайшее расстояние между двумя точками – это длина отрезка, их соединяющего.

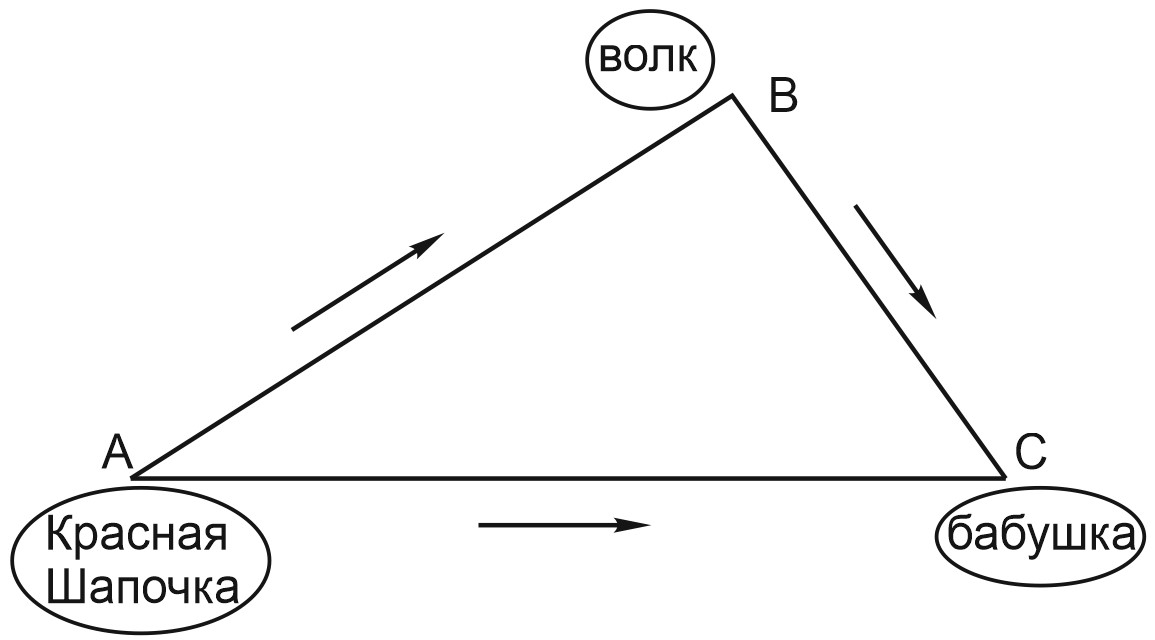
Посмотрим, как признаки равенства треугольников применяются в задачах ОГЭ.

1. В равнобедренном треугольнике \(ABC\) с основанием \(AB\) проведены \(AM\) и \(BN\) – биссектрисы углов.

Докажите, что \(AM=BN\).

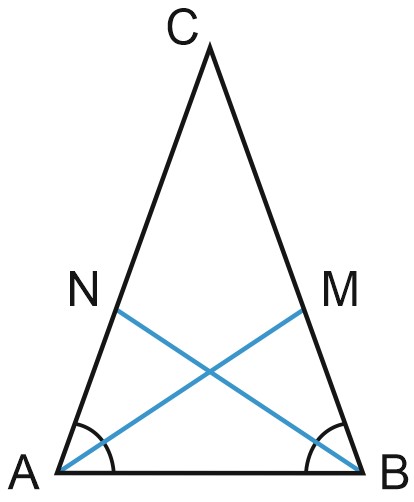
Доказательство:

Треугольники \(AMB\) и \(BNA\) – равны по стороне и двум прилежащим к ней углам.

\(\angle CAB=\angle CBA\), потому что треугольник \(ABC\) равнобедренный.

\(AB\) – общая сторона,

\(\angle MAB=\angle NBA=\frac{1}{2}\angle CAB.\)

Следовательно, \( AM=BN.\)

2. Докажите, что если в треугольнике высота является биссектрисой, то треугольник равнобедренный.

Доказательство:

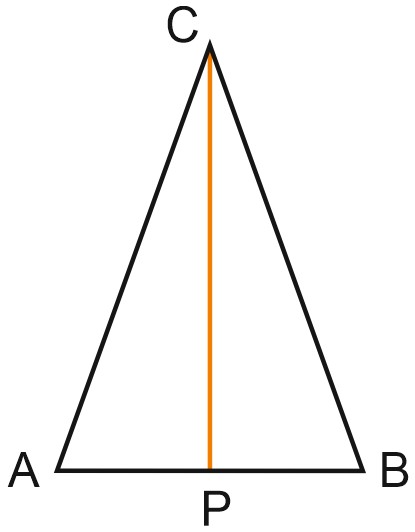
Доказательство:

\(\triangle APC=\triangle BPC\) по стороне и двум углам;

\(\angle APC=\angle BCP\), потому что \(CP\) – биссектриса треугольника \(ABC\);

\(\angle CPA=\angle CPB=90^{\circ}\), так как \(CP\) – высота.

\(CP\) – общая сторона треугольников \(APC\) и \(BPC\).

Следовательно, \(AC=BC\), треугольник \(ABC\) – равнобедренный.

3. Треугольники расположены так, как показано на рисунке, \(AO=BO\) и \(CO=DO\).

Докажите, что \(\triangle AOC=\triangle BOD\).

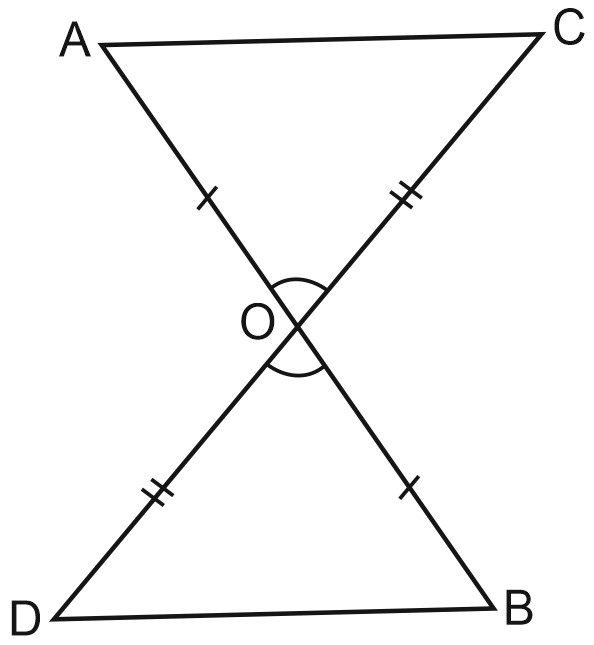
Доказательство:

\(\angle AOC=\angle BOD\) как вертикальные.

Следовательно, \(\triangle AOC=\triangle BOD\) по двум сторонам и углу между ними.

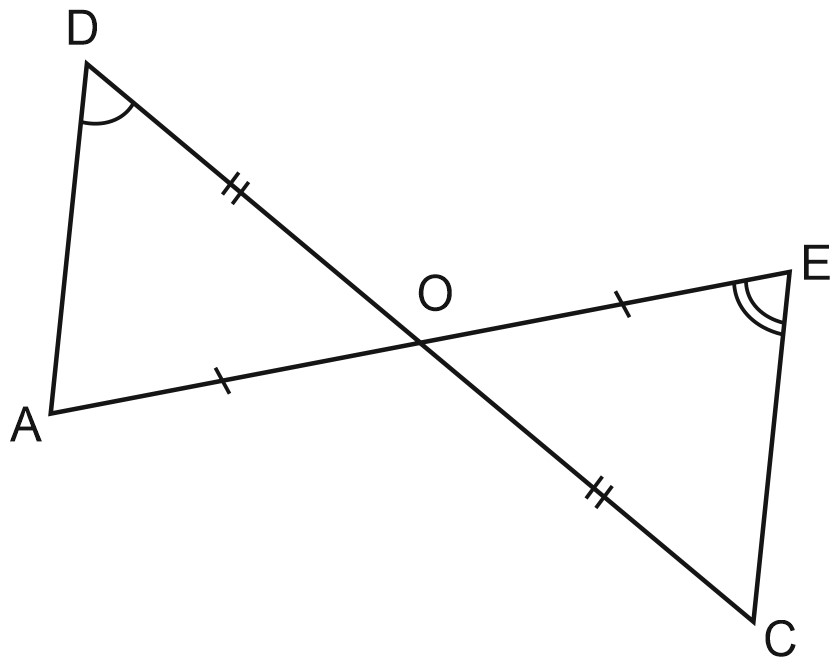
4. Дано: \(AE\cap DC=O; \; AO=EO, \; \angle D=47^{\circ}; \; DO=CO, \; \angle E=42^{\circ}.\)

Докажите, что \(\triangle ADO=\triangle ECO,\) и найдите \(\angle A, \; \angle C.\)

Решение:

Рассмотрим \(\triangle ADO\) и \(\triangle OEC\).

\(AO=EO\) по условию;

\(DO=CO\) по условию;

\(\angle AOD=\angle EOC\) как вертикальные.

\(\triangle ADO=\triangle ECO\) по двум сторонам и углу между ними.

В равных треугольниках соответственные углы равны, потому \(\angle A=\angle E=42^{\circ}, \; \angle D=\angle C=47^{\circ}.\)

Ответ: \(\angle A=42^{\circ}, \; \angle D=47^{\circ}.\)

5. Дана трапеция \(ABCD, \; AB=CD, \; AC=BD, \; \angle BAC=30^{\circ}.\) Найдите \(\angle CDB.\)

Решение:

\(\triangle BAC=\triangle CDB\) по трем сторонам.

В них \(BC\) – общая сторона, \(AB=CD\) по условию, \(AC=BD\) по условию.

\(\angle CDB=\angle BAC=30^{\circ}\).

Это следует из равенства треугольников. Оба угла лежат против общей стороны \(BC\).

Ответ: 30.

6. В треугольнике \(ABC\) проведена биссектриса \(AD\) и \(AB=AD=CD\). Найдите меньший угол
треугольника \(ABC\). Ответ дайте в градусах.

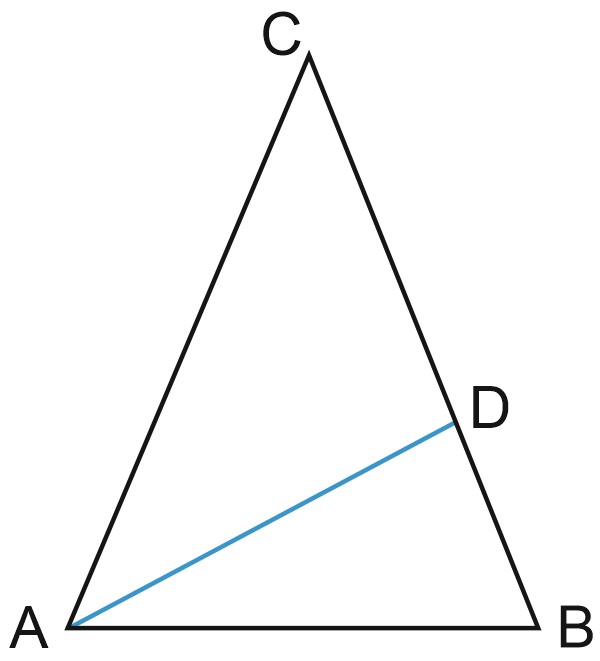
Решение:

По условию, трекгольники \(ADC\) и \(ADB\) – равнобедренные.

\(\angle DAC=\angle ACD, \; \angle ADB=\angle ABD\) как углы при основания у равнобедренных треугольников

Обозначим угол \(BAD\) за \(x\).

Из равнобедренного треугольника \(ABD\): угол \(ABD\) равен \(\displaystyle\frac{1}{2}\cdot (180^{\circ}-x).\)

С дургой стороны, этот угол равен углу \(BAC\), то есть \(2x\).

Получим:

\(2x=\displaystyle\frac{1}{2}\cdot (180^{\circ}-x).\)

Отсюда \(x=36^{\circ}.\)

Ответ: 36.