Системы линейных уравнений

Линейным уравнением с двумя переменными называется уравнение вида \(ax+by=c\), где \(a\), \(b\), \(c\) — числа, \(x\), \(y\) — переменные. Числа \(a\) и \(b\) называются коэффициентами.

Пара значений переменных \((x, y)\), обращающая уравнение в верное равенство, называется решением уравнения.

Например, пары \((10; 0)\), \((-2; -4)\) являются решениями уравнения \(x-3y=10\), а пара \((1; 5)\) решением данного уравнения не является. Потому что, если в уравнение подставить \(x=10\) и \(y = 0\), получим верное равенство. А если подставить \(x=1\) и \(y =5\), получится, что \(1- 15= 10\). Это неверно.

Система линейных уравнений.

Если два уравнения объединены фигурной скобкой, то это система уравнений. 

Фигурная скобка ставится, когда надо найти значения переменных, которые будут решениями и первого, и второго уравнения.

Например, \(\left\{\begin{matrix}
2x+3y=5, \\
3x-y=-9\end{matrix}\right.\) – система линейных уравнений с двумя переменными.

Решение системы уравнений с двумя переменными \(x\) и \(y\) - это пара значений переменных \((x; y)\), обращающая каждое уравнение в верное равенство.

Например, пара \((-2; 3)\) является решением указанной выше системы.

Решить систему уравнений – значит найти все ее решения или доказать, что решений нет.

Есть несколько способов решения систем линейных уравнений. Это способ подстановки, метод сложения и графический способ.

1. Способ подстановки.

\(1)\) Выражаем из какого-либо уравнения системы одну переменную через другую.

\(2)\) Подставляем полученное выражение для этой переменной в другое уравнение.

\(3)\) Решаем полученное уравнение с одной переменной.

\(4)\) Находим соответствующее значение второй переменной.

Пример 1. Решить систему: \(\left\{\begin{matrix}
4x+y=6, \\
3x+2y=2.\end{matrix}\right.\)

Решение:

\(1)\) Из первого уравнения выразим переменную \(y\): \(y=6-4x\).

\(2)\) Подставив выражение \(6-4x\) вместо переменной y во второе уравнение, получим уравнение \(3x+2(6-4x)=2\).

И получим систему: \(\left\{\begin{matrix}
y=6-4x, \\
3x+2(6-4x)=2.\end{matrix}\right.\)

\(3)\) Решив отдельно последнее уравнение с переменной \(x\), получим \(x=2\).

\(4)\) Найдем соответствующее значение переменной \(y=6-4\cdot 2=-2\).

Ответ: \((2; -2).\)

2. Способ сложения.

Он основан на том, что уравнения в системе можно складывать друг с другом. Левую часть первого - с левой частью второго, правую часть первого - с правой частью второго.

Также можно умножать обе части уравнения на любое число, не равное нулю.

Алгоритм решения систем уравнений методом сложения:

\(1)\) Если нужно, умножаем уравнения системы на такие числа, чтобы коэффициенты при одной из переменных стали противоположными числами.

\(2)\) Складываем уравнения системы.

\(3)\) Решаем полученное уравнение с одной переменной.

\(4)\) Находим соответствующее значение второй переменной из любого уравнения.

Пример 2. Решить систему уравнений: \(\left\{\begin{matrix}
2x+3y=7, \\
3x-y=16.\end{matrix}\right.\)

Решение:

\(1)\) Умножив обе части второго уравнения системы на \(3\), получим систему \(\left\{\begin{matrix}
2x+3y=7, \\
9x-3y=48.\end{matrix}\right.\)

\(2)\) Сложив оба уравнения системы, получим уравнение: \(2x+9x+3y-3y=7+48.\)

\(3)\) Приведем подобные в уравнении: \(11x=55\), отсюда \(x=5.\)

\(4)\) Подставим это значение для \(x\), например, во второе уравнение исходной системы \(3x-y=16\).

Получим уравнение \(3\cdot 5-y=16\). Находим \(y=-1.\)

Ответ: \((5; -1).\)

3. Графический способ.

Этот способ основан на построении графиков уравнений.

Графиком линейного уравнения с двумя переменными является прямая. А для задания прямой достаточно двух точек.

Алгоритм графического способа решения систем уравнений:

\(1)\) Строим график первого уравнения.

\(2)\) В той же системе координат строим график второго уравнения.

\(3)\) Находим координаты точки пересечения графиков.

Координаты точки пересечения графиков являются решением системы уравнений.

На плоскости возможны три случая взаимного расположения двух прямых – графиков уравнений системы.

\(1)\) Прямые пересекаются, т. е. имеют одну общую точку. Тогда система уравнений имеет единственное решение.

\(2)\) Прямые параллельны, т. е. не имеют общих точек. Тогда система уравнений не имеет решений.

\(3)\) Прямые совпадают. Тогда система уравнений имеет бесконечно много решений.

Заметим, что при графическом способе решения системы уравнений обычно получается приближённое решение. Для проверки мы подставляем координаты найденной точки в систему уравнений. Если получаем верные равенства, значит, все правильно.

Пример 3. Решить систему уравнений: \(\left\{\begin{matrix}
2x-y=8, \\
3x+2y=5.\end{matrix}\right.\)

\(1)\) Построим график уравнения \(2x-y=8.\)

Графиком линейного уравнения является прямая. Прямая определяется двумя точками. Найдем координаты двух любых точек прямой из уравнения.

Если \(x=0\), \(y=-8\), а если \(y=0\), то \(x=4\).

В системе координат отметим точки \((0; -8)\) и \((4; 0)\). Проведем через них прямую.

Она является графиком первого уравнения.

\(2)\) Построим график уравнения \(3x+2y=5\).

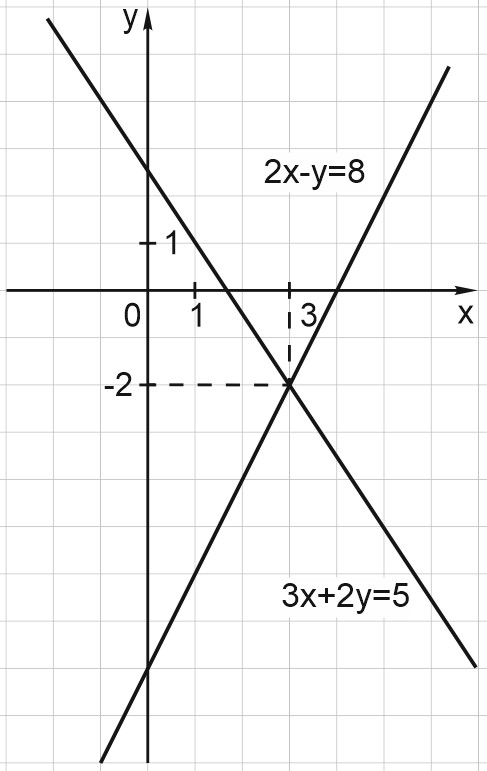
Найдем координаты любых двух точек этой прямой. Если \(x=1\), то \(y=1\), если \(x=3\), то \(y=-2\).

В той же системе координат отметим точки \((1; 1)\) и \((3; -2)\). Проведем через них прямую.

Она является графиком второго уравнения.

\(3)\) Полученные прямые пересекаются в точке \((3; -2)\). Сделаем проверку. Подставим значения \(x=3\) и \(y=-2\) в систему, получим верные равенства.

Значит \((3; -2)\) – решение системы.

Ответ: \((3; -2).\)