Задание 10 ОГЭ по математике. Вероятность и статистика.

Джамиля Агишева

Задание 10 ОГЭ по математике – это задача по теории вероятностей.

Теория вероятностей рассматривает случайные действия, явления, процессы, исход которых заранее неизвестен. Например, высаживая семена огурцов, мы проводим эксперимент. В результате из десяти семечек может взойти от 0 до 10 ростков, т.е. случайное количество.

Событие – результат некоторого действия. Случайное событие – событие, которое может произойти или не произойти в данном эксперименте. Например, проигрыш или выигрыш нашей любимой футбольной команды заранее предсказать невозможно – это стечение обстоятельств, а сам исход игры мы узнаем по её окончании.

События принято обозначать заглавными латинскими буквами: \( A, \ B, \ C\) и т.д.

Пример: \( A\) – взошло ровно 9 ростков из десяти посаженных семян огурцов. Оно может произойти или не произойти.

Вероятность события \( P(A)\)– это отношение числа  исходов, благоприятствующих событию , к числу всех исходов, возможных в данном эксперименте. Итак,

\( P\left(A\right)=\displaystyle \frac{m}{n}.\)

Имейте в виду, что числитель такой дроби не может быть больше знаменателя, а значит, вероятность всегда меньше либо равна 1.

Приступим к решению задач.

1. Бабушка испекла одинаковые на вид пирожки: 7 с мясом, 8 с капустой и 5 с яблоками. Внучка Даша наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с мясом.

Выбор пирожка – несомненно, испытание для Даши. А вдруг попадётся нелюбимый, с капустой?

Решение:

Событие \(A\) – достался пирожок с мясом. Найдём \(m\) и \(n\).

\(m\) – число исходов, благоприятствующих событию \(A\).

\(n\) – число всех исходов, возможных в данном эксперименте.

Давайте перефразируем на языке пирожков: \(m\) – количество пирожков с мясом, т.е. \(m=7, \ n\)  – количество всех испечённых пирожков, т. е. \(n=7+8+5=20.\)

Осталось найти вероятность. Вспомним формулу и вычислим. Итак, \(P\left(A\right)=\displaystyle \frac{m}{n}=\frac{7}{20}=0,35.\)

Замечание: не забудьте ответ представить в виде десятичной дроби!

Ответ: 0,35.

Давайте рассмотрим задачу посложнее.

2. В коробке хранятся жетоны с номерами от 5 до 54 включительно. Какова вероятность того, что на извлечённом наугад из коробки жетоне написано двузначное число?

Решение:

Событие \(A\) – извлечённый наугад жетон содержит двузначное число. Найдём \(m\) и \(n\).

\(m\) – число жетонов с двузначным номером, \(n\) – число всех жетонов.

Сначала определимся с \(n\). Типичная ошибка считать так: \(n=54-5=49\). На самом деле когда-то были жетоны от 1 до 54. Но номера 1, 2, 3 и 4 со временем потерялись, т.е. пропало четыре штуки. Тогда,  \(n=54-4=50\).

Сколько жетонов с двузначными номерами? Всего 50, номера 5, 6, 7, 8, 9 (их пять штук) – однозначные. Тогда, \(m=50-5=45\).

Итак, \(P\left(A\right)=\displaystyle \frac{m}{n}=\frac{45}{50}=\frac{9}{10}=0,9.\)

Ответ: 0,9.

3. В лыжных гонках участвуют 10 спортсменов из России, 8 спортсменов из Швеции и 7 спортсменов из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что спортсмен из Швеции будет стартовать последним.

Решение:

Событие \(A\) – спортсмен из Швеции будет стартовать последним.

\(m=8\) – число спортсменов из Швеции, \(n=10+8+7=25\) – число всех спортсменов.

Т.к. старт определяется жребием, то не важно, под каким стартовым номером будет выступать тот или иной лыжник, под вторым или последним.

Итак, \(P\left(A\right)=\displaystyle \frac{m}{n}=\frac{8}{25}=0,32.\)

Ответ: 0,32.

4. Оля наугад выбирает трёхзначное число. Найдите вероятность того, что оно делится на 51.

Решение:

Событие \(A\) – выбранное число делится на 51. Найдём \(m\) и \(n\).

\(m\) – количество трёхзначных чисел, кратных 51, \(n\) – число всех трёхзначных чисел.

Последнее трёхзначное число 999. Найдём все числа, кратные 51 среди чисел от 1 до 999 (их даже можно попробовать пересчитать непосредственно: 51, 102, 153, …, 969). Разделим 999 на 51.

Получим: \(999:51=19\displaystyle \frac{30}{51},\) т.е. ровно 19 чисел, кратных 51. Но среди этого количества окажется двузначное число 51, которое не учитывается в задаче, значит, \(m=18\).

Теперь определим \(n\). Чисел от 1 до 999 ровно 999, исключим из них однозначные и двузначные числа от 1 до 99. Таким образом,  .

Итак, \(P\left(A\right)=\displaystyle \frac{m}{n}=\frac{18}{900}=\frac{2}{100}=0,02.\)

Ответ: 0,02.

5. Фабрика выпускает сумки. В среднем на 200 качественных сумок приходится двадцать сумок с дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Обратите внимание на условие задачи. Здесь не говорится, что из 200 сумок двадцать – с дефектами. В тексте чётко обозначено, что качественных – 200 штук, а некачественных – 20 штук.

Решение:

Событие \(A\) – купленная сумка окажется качественной. Найдём \(m\) и \(n\).

Всё просто, \(m=200, \ n=200+20=220\).

Итак, \(P\left(A\right)=\displaystyle \frac{m}{n}=\frac{200}{220}=\frac{10}{11}.\)

Что-то пошло не так? Полученный результат невозможно будет записать в бланк ответов, т.к. ответом может быть либо целое число, либо конечная десятичная дробь. Ещё раз внимательно перечитываем задачу, а точнее, вопрос задачи. Там сказано: результат округлите до сотых. Помним, калькулятор использовать нельзя. Честно делим в столбик. Т.к. округлить нужно до сотых, то мы найдём три цифры после запятой и только потом запишем результат.

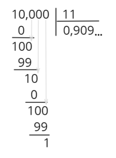
Получаем: \(\displaystyle \frac{10}{11}\approx 0,909...\approx 0,91.\)

Ответ: 0,91.

Больше задач по теории вероятностей: Определение вероятности и  Теория вероятностей. Дерево возможных исходов.