5. Четырехугольник \(ABCD\) вписан в окружность. Угол \(ABC\) равен \(92^{\circ}\), угол \(CAD\) равен \(60^{\circ}.\) Найдите угол \(ABD.\) Ответ дайте в градусах.
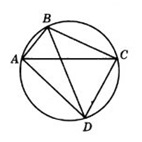
Решение:
\(\angle ABD\) – вписанный. Он опирается на дугу \(AD\) и равен половине этой дуги. Находим величину дуги \(AD.\)
\(\angle ABC\) – вписанный. Он опирается на дугу \(ADC.\) Величина дуги \(ADC\) равна \(92^{\circ} \cdot 2 = 184^{\circ}.\)
\(\angle CAD\) – вписанный. Он опирается на дугу \(DC.\) Значит, величина дуги \(DC\) равна \(60^{\circ} \cdot 2 = 120^{\circ}.\)
Величина дуги \(AD\) равна разности величин дуг \(ADC\) и \(DC.\) Получим:
\(184^{\circ} - 120^{\circ} = 64^{\circ}.\)
\(\angle ABD = 64^{\circ} : 2= 32^{\circ}.\)
Ответ: \(32^{\circ}.\)
6. В треугольнике \(ABC\) известно, что \(AC = 16, \ BC = 12,\) угол \(C\) равен \(90^{\circ}.\) Найдите радиус описанной около этого треугольника окружности.
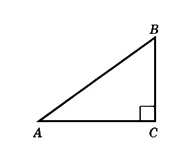
Решение:
Центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина - радиусом.
По теореме Пифагора найдем гипотенузу \(AB:\)
\(AB^{2}=BC^{2}+AC^{2}=12^{2}+16^{2}=144+256=400;\)
\(AB =\sqrt{400}=20.\)
Гипотенуза равна 20, значит радиус равен 10.
Ответ: 10
В варианте ЕГЭ-2025 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
