Задание 26 ОГЭ по Математике. Комплексная геометрическая задача

15. Биссектриса \(CM\) треугольника \(ABC\) делит сторону \(AB\) на отрезки \(AM=5\) и \(MB=10.\) Касательная к описанной окружности треугольника \(ABC\), проходящая через точку \(C\), пересекает прямую \(AB\) в точке \(D.\) Найдите \(CD.\)

Решение:

Построим чертеж:

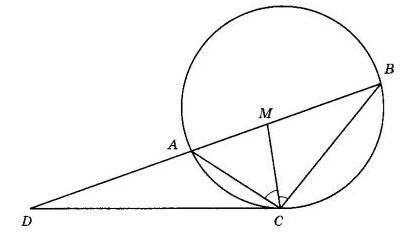
Угол между касательной \(CD\) и хордой \(AC\) равен половине угловой величины дуги \(AC\), заключенной между сторонами этого угла.

Вписанный угол \(ABC\) также равен половине угловой величины дуги АС, на которую он опирается.

Значит, углы \(ACD\) и \(DBC\) равны. Тогда треугольники \(ACD\) и \(CBD\) подобны по двум углам (угол \(D\) у них общий).

Запишем соотношение сходственных сторон треугольников \(ACD\) и \(CBD:\)

\(\displaystyle \frac{AD}{CD}=\frac{CD}{BD}=\frac{AC}{BC}.\)

Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.

Значит, \(\displaystyle \frac{AC}{BC}=\frac{5}{10}=\frac{1}{2}.\)

Пусть \(AD=x, \ CD=y.\) Получим:

\(\displaystyle \frac{x}{y}=\frac{y}{x+15}=\frac{1}{2}.\)

Отсюда \(2y=\displaystyle \frac{y}{2}+15; \ y=10.\)

Ответ: 10.

<< Назад к списку задач