Задача 6 ОГЭ по математике называется «Числа и вычисления». Это действия с обыкновенными и с десятичными дробями. Действия со степенями. Сравнение чисел.
Приступим к решению задач.
1. Найдите значение выражения \(\displaystyle \frac{0,8}{1-\frac{1}{9}}.\)
Решение:
Вспоминаем, что при вычитании дробей нужно их привести к общему знаменателю, а при делении дробей первую из них умножаем на перевёрнутую вторую.
Посчитаем, чему равен знаменатель: \(1-\displaystyle \frac{1}{9}=\frac{9}{9}-\frac{1}{9}=\frac{8}{9}.\)
Получим: \(\displaystyle \frac{0,8}{1-\frac{1}{9}}=\displaystyle \frac{8}{10}:\frac{8}{9}=\displaystyle \frac{8}{10}\cdot \frac{9}{8}=\frac{9}{10}=0,9.\)
Ответ: 0,9.
2. Соотнесите обыкновенные дроби с равными им десятичными дробями.
| А. \(\displaystyle \frac{5}{8}\) | Б. \(\displaystyle \frac{3}{25}\) | В. \(\displaystyle \frac{1}{2}\) | Г. \(\displaystyle \frac{1}{50}\) |
| 1) 0,5 | 2) 0,02 | 3) 0,12 | 4) 0,625 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Решение:
Каждую из данных обыкновенных дробей можно представить в виде десятичной, например, используя деление в столбик.
 |
 |
 |
 |
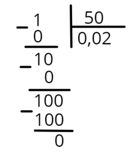| \(\displaystyle \frac{5}{8}=0,625\) | \(\displaystyle \frac{3}{25}=0,12\) | \(\displaystyle \frac{1}{2}=0,5\) | \(\displaystyle \frac{1}{50}=0,02\) |
Итак, деление выполнено. Сопоставим полученные результаты:
| А | Б | В | Г |
| 4 | 3 | 1 | 2 |
Ответ: 4312.
Замечание 1. Преобразование обыкновенных дробей в десятичные можно произвести и без деления в столбик. Т. к. любая десятичная дробь записывается как обыкновенная со знаменателем 10, 100, 1000 и т. д., то данные обыкновенные дроби можно «доделать» до десятичных. Для этого используем основное свойство дроби: дробь не изменится, если её числитель и знаменатель домножить на одно и тоже число.
\(\displaystyle \frac{5}{8}=\frac{5}{2\cdot 2\cdot 2}=\frac{5\cdot 5\cdot 5\cdot 5}{2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5}=\frac{625}{1000}=0,625; \; \; \; \; \displaystyle \frac{1}{2}=\frac{1\cdot 5}{2\cdot 5}=\frac{5}{10}=0,5;\)
\(\displaystyle \frac{3}{25}=\frac{3}{5\cdot 5}=\frac{3\cdot 2\cdot 2}{5\cdot 2\cdot 5\cdot 2}=\frac{12}{100}=0,12; \; \; \; \; \; \; \; \; \; \; \displaystyle \frac{1}{50}=\frac{1}{10\cdot 5}=\frac{1\cdot 2}{10\cdot 5\cdot 2}=\frac{2}{100}=0,02.\)
Замечание 2. В этой задаче можно было, наоборот, преобразовывать заданные десятичные дроби в обыкновенные путём упрощения, т. е. сокращения числителя и знаменателя.
\(0,5=\displaystyle \frac{5}{10}=\frac{1}{2}\) (сократили на 5); \(\; 0,02=\displaystyle \frac{2}{100}=\frac{1}{50}\) (сократили на 2);
\(0,12=\displaystyle \frac{12}{100}=\frac{3}{25}\) (сократили на 4); \(\; 0,625=\displaystyle \frac{625}{1000}=\frac{125}{200}=\frac{25}{40}=\frac{5}{8}\)
(сократили последовательно три раза на 5).
Выбирайте любой способ. Здесь важен правильный результат!
Для выполнения следующих заданий нам потребуются свойства степеней. Напомним основные из них.
Степенью называется выражение вида \(\boldsymbol{a^c.}\)
Здесь \(a\) — основание степени, \(c\) — показатель степени.
По определению, \(a^1=a.\)
Возвести число в квадрат — значит умножить его само на себя: \(a^2=a\cdot a.\)
Возвести число в куб — значит умножить его само на себя три раза: \(a^3=a\cdot a\cdot a.\)
Возвести число в натуральную степень \(n\) — значит умножить его само на себя \(n\) раз:
\(a^n=\underbrace{a\cdot a\cdot a\cdot a\cdot \dots \cdot a}_{n}.\)
По определению, \({a}^0=1.\)
Это верно для \(a\ne 0.\) Выражение \(0^0\) не определено.
Определим, что такое степень с целым отрицательным показателем.
\(a^{-1}=\displaystyle \frac{1}{a};\)
\(a^{-2}=\displaystyle \frac{1}{a^2};\)
\(a^{-n}=\displaystyle \frac{1}{a^n}.\)
Конечно, все это верно для \(a\ne 0,\) поскольку на ноль делить нельзя.
Соберем свойства степеней и основные формулы в одной таблице.
| \(a^0=1\) | |
| \(a^n\cdot a^m=a^{n+m}\) | При перемножении степеней с одинаковыми основаниями показатели степеней складываются. |
|
\(\displaystyle \frac{a^n}{a^m}=a^{n-m}\) |
При делении степеней с одинаковыми основаниями показатели степеней вычитаются. |
|
\((a^n)^m=a^{n\cdot m}\) |
При возведении степени в степень показатели степеней перемножаются. |
| \(a^{-n}=\displaystyle \frac{1}{a^n}\) | При возведении в отрицательную степень получаем дробь, где единица делится на степень с положительным показателем. |
| \((a\cdot b)^n=a^n \cdot b^n\) | При возведении произведения двух множителей в степень каждый из этих множителей возводится в заданную степень. |
| \(\left (\displaystyle \frac{a}{b}\right )^n=\displaystyle \frac{a^n}{b^n}\) | При возведении дроби в степень получается дробь, числитель и знаменатель которой возведены в заданную степень. |
| \(\left (\displaystyle \frac{a}{b}\right )^{-n}=\left (\displaystyle \frac{b}{a}\right )^n\) | При возведении дроби в отрицательную степень дробь переворачивается, а показатель степени становится положительным. |
3. Найдите значение выражения \({{(16\cdot 10}^{-2})}^2\cdot {(13\cdot 10}^4).\)
Решение:
Вычислим, используя свойства степеней:
\({{(16\cdot 10}^{-2})}^2\cdot {(13\cdot 10}^4)={16}^2\cdot {\left({10}^{-2}\right)}^2\cdot {13\cdot 10}^4=256\cdot 13\cdot ({10}^{-4}\cdot {10}^4)=3\ 328\cdot {10}^0=3328.\)
Ответ: 3328.
4. Найдите значение выражения \({5\cdot 10}^{-1}+{6\cdot 10}^{-2}+{4\cdot 10}^{-4}.\)
Решение:
Вычислим, используя свойства степеней:
\( {5\cdot 10}^{-1}+{6\cdot 10}^{-2}+{4\cdot 10}^{-4}=5\cdot \displaystyle \frac{1}{{10}^1}+6\cdot \frac{1}{{10}^2}+4\cdot \frac{1}{{10}^4}=\)
\(=5\cdot 0,1+6\cdot 0,01+4\cdot 0,0001=0,5+0,06+0,0004=0,5604.\)
Ответ: 0,5604.
5. Найдите значение выражения \(\displaystyle \frac{3^8\cdot 3^5}{3^9}.\)
Решение:
Вычислим, используя свойства степеней:
\(\displaystyle \frac{3^8\cdot 3^5}{3^9}=\displaystyle \frac{3^{8+5}}{3^9}=\frac{3^{13}}{3^9}=3^{13-9}=3^4=81.\)
Ответ: 81.
В варианте ЕГЭ-2025 две задачи по теории вероятностей — это №4 и №5. По заданию 5 в Интернете почти нет доступных материалов. Но в нашем бесплатном мини-курсе все это есть.
