Центр подготовки к ЕГЭ > Тонкие линзы. Построение изображений.

Тонкие линзы. Построение изображений.

Оглавление:

Собирающая линза: действительное изображение точки.
Собирающая линза: действительное изображение предмета.
Собирающая линза: мнимое изображение точки.
Собирающая линза: мнимое изображение предмета.
Собирающая линза: предмет в фокальной плоскости.
Рассеивающая линза: мнимое изображение точки.
Рассеивающая линза: мнимое изображение предмета.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: построение изображений в линзах, формула тонкой линзы.

Правила хода лучей в тонких линзах, сформулированные в предыдущей теме, приводят нас к важнейшему утверждению.

Теорема об изображении. Если перед линзой находится светящаяся точка $S$ , то после преломления в линзе все лучи (или их продолжения) пересекаются в одной точке $S{}$ .

Напомним ещё раз, что это касается не вообще всех лучей, а только параксиальных, то есть образующих малые углы с главной оптической осью. В предыдущей теме мы договорились, что рассматриваем только параксиальные лучи. Лишь для них работают наши правила хода лучей сквозь тонкие линзы.

Точка $S{}$ называется изображением точки $S$ .

Если в точке $S{}$ пересекаются сами преломлённые лучи, то изображение называется действительным. Оно может быть получено на экране, так как в точке $S{}$ концентрируется энергия световых лучей.

Если же в точке $S{}$ пересекаются не сами преломлённые лучи, а их продолжения (так бывает, когда преломлённые лучи расходятся после линзы), то изображение называется мнимым. Его нельзя получить на экране, поскольку в точке $S{}$ не сосредоточено никакой энергии. Мнимое изображение, напомним, возникает благодаря особенности нашего мозга - достраивать расходящиеся лучи до их мнимого пересечения и видеть в этом пересечении светящуюся точку.Мнимое изображение существует лишь в нашем сознании.

Теорема об изображении служит основой построения изображений в тонких линзах. Мы докажем эту теорему как для собирающей, так и для рассеивающей линзы.

к оглавлению ▴

Собирающая линза: действительное изображение точки.

Сперва рассмотрим собирающую линзу. Пусть $a$ - расстояние от точки $S$ до линзы, $f$ - фокусное расстояние линзы. Имеются два принципиально разных случая: $a>f$ и $a<f$ (а также промежуточный случай $a=f$ ). Мы разберём эти случаи поочерёдно; в каждом из них мы
обсудим свойства изображений точечного источника и протяжённого объекта.

Первый случай: $a>f$ . Точечный источник света $S$ расположен дальше от линзы, чем левая фокальная плоскость (рис. 1).

Рис. 1. Случай a>f: действительное изображение точки S

Луч $SO$ , идущий через оптический центр, не преломляется. Мы возьмём произвольный луч $SX$ , построим точку $S{}$ , в которой преломлённый луч пересекается с лучом $SO$ , а затем покажем, что положение точки $S{}$ не зависит от выбора луча $SX$ (иными словами, точка $S{}$ является одной и той же для всевозможных лучей $SX$ ). Тем самым окажется, что все лучи, исходящие из точки $S$ , после преломления в линзе пересекаются в точке $S{}$ и теорема об изображении будет доказана для рассматриваемого случая $a>f$ .

Точку $S{}$ мы найдём, построив дальнейший ход луча $SX$ . Делать это мы умеем: параллельно лучу $SX$ проводим побочную оптическую ось $OP$ до пересечения с фокальной плоскостью в побочном фокусе $P$ , после чего проводим преломлённый луч $XP$ до пересечения с лучом $SO$ в точке $S{}$ .

Теперь будем искать расстояние $b$ от точки $S{}$ до линзы. Мы покажем, что это расстояние выражается только через $a$ и $f$ , т. е. определяется лишь положением источника и свойствами линзы, и не зависит тем самым от конкретного луча $SX$ .

Опустим перпендикуляры $SA$ и $S{}$ на главную оптическую ось. Проведём также $SK$ параллельно главной оптической оси, т. е. перпендикулярно линзе. Получим три пары подобных треугольников:

$\triangle SAO \sim \triangle S{}$ , (1)
$\triangle SXS{}$ , (2)
$\triangle SXK \sim \triangle OPF$ . (3)

В результате имеем следующую цепочку равенств (номер формулы над знаком равенства указывает, из какой пары подобных треугольников данное равенство получено).

$\frac{\displaystyle AO}{\displaystyle OA{}$ (4)

Но $AO=SK=a, OA{}$ , так что соотношение (4) переписывается в виде:

$\frac{\displaystyle a}{\displaystyle b}=\frac{\displaystyle a}{\displaystyle f}-1$ . (5)

Отсюда находим искомое расстояние от точки $S{}$ до линзы:

$b=\frac{\displaystyle af}{\displaystyle a-\displaystyle f}$ . (6)

Как видим, оно и в самом деле не зависит от выбора луча $SX$ . Следовательно, любой луч $SX$ после преломления в линзе пройдёт через построенную нами точку $S{}$ , и эта точка будет действительным изображением источника $S$

Теорема об изображении в данном случае доказана.

Практическая важность теоремы об изображении состоит вот в чём. Коль скоро все лучи источника $S$ пересекаются после линзы в одной точке - его изображении $S{}$ - то для построения изображения достаточно взять два наиболее удобных луча. Какие именно?

Если источник $S$ не лежит на главной оптической оси, то в качестве удобных лучей годятся следующие:

- луч, идущий через оптический центр линзы - он не преломляется;
- луч, параллельный главной оптической оси - после преломления он идёт через фокус.

Построение изображения с помощью этих лучей показано на рис. 2.

Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси

Если же точка $S$ лежит на главной оптической оси, то удобный луч остаётся лишь один - идущий вдоль главной оптической оси. В качестве второго луча приходится брать "неудобный" (рис. 3).

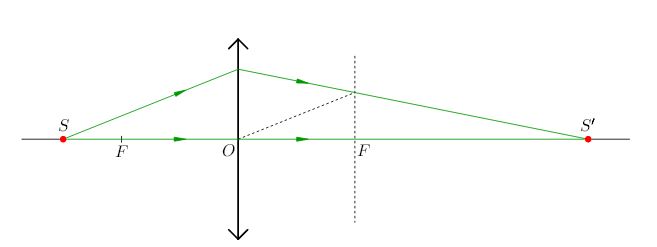Рис. 3. Построение изображения точки S, лежащей на главной оптической оси

Посмотрим ещё раз на выражение ( 5). Его можно записать в несколько ином виде, более симпатичном и запоминающемся. Перенесём сначала единицу влево:

$1+\frac{\displaystyle a}{\displaystyle b}=\frac{\displaystyle a}{\displaystyle f}.$

Теперь разделим обе части этого равенства на a:

$\frac{\displaystyle 1}{\displaystyle a}+\frac{\displaystyle 1}{\displaystyle b}=\frac{\displaystyle 1}{\displaystyle f}.$ (7)

Соотношение (7) называется формулой тонкой линзы (или просто формулой линзы). Пока что формула линзы получена для случая собирающей линзы и для $a>f$ . В дальнейшем мы выведем модификации этой формулы для остальных случаев.

Теперь вернёмся к соотношению (6). Его важность не исчерпывается тем, что оно доказывает теорему об изображении. Мы видим также, что $b$ не зависит от расстояния $SA$ (рис. 1, 2) между источником $S$ и главной оптической осью!

Это означает, что какую бы точку $M$ отрезка $SA$ мы ни взяли, её изображение будет находиться на одном и том же расстоянии $b$ от линзы. Оно будет лежать на отрезке $S{}$ - а именно, на пересечении отрезка $S{}$ с лучом $MO$ , который пойдёт сквозь линзу без преломления. В частности, изображением точки $A$ будет точка $A{}$ .

Тем самым мы установили важный факт: изображением отрезка $SA$ лужит отрезок $S{}$ . Отныне исходный отрезок, изображение которого нас интересует, мы называем предметом и обозначаем на рисунках красной стрелочкой. Направление стрелки нам понадобится для того, чтобы следить - прямым или перевёрнутым получается изображение.

к оглавлению ▴

Собирающая линза: действительное изображение предмета.

Перейдём к рассмотрению изображений предметов. Напомним, что пока мы находимся в рамках случая $a>f$ . Здесь можно выделить три характерных ситуации.

1. $f<a<2f$ . Изображение предмета является действительным, перевёрнутым, увеличенным (рис. 4; двойной фокус обозначен $2F$ ). Из формулы линзы следует, что в этом случае будет $b>2f$ (почему?).

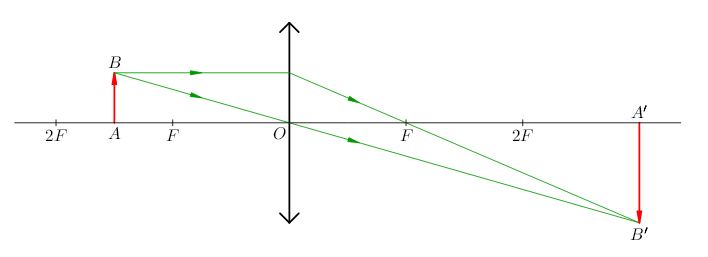Рис. 4. $f<a<2f$ : изображение действительное, перевёрнутое, увеличенное

Такая ситуация реализуется, например, в диапроекторах и киноаппаратах - эти оптические приборы дают на экране увеличенное изображение того, что находится на плёнке. Если вам доводилось показывать слайды, то вы знаете, что слайд нужно вставлять в проектор перевёрнутым - чтобы изображение на экране выглядело правильно, а не получилось вверх ногами.

Отношение размера изображения к размеру предмета называется линейным увеличением линзы и обозначается Г - (это заглавная греческая "гамма"):

$\Gamma =\frac{\displaystyle A{}$ .

Из подобия треугольников $\triangle ABO$ и $\triangle A{}$ получим:

$\Gamma =\frac{\displaystyle A{}$ . (8)

Формула (8) применяется во многих задачах, где фигурирует линейное увеличение линзы.

2. $a=2f$ . В этом случае из формулы (6) находим, что и $b=2f$ . Линейное увеличение линзы согласно (8) равно единице, т. е. размер изображения равен размеру предмета (рис. 5).

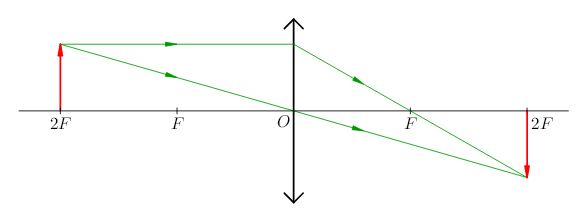Рис. 5.a=2f: размер изображения равен размеру предмета

3. $a>2f$ . В этом случае из формулы линзы следует, что $b<2f$ (почему?). Линейное увеличение линзы будет меньше единицы - изображение действительное, перевёрнутое, уменьшенное (рис. 6).

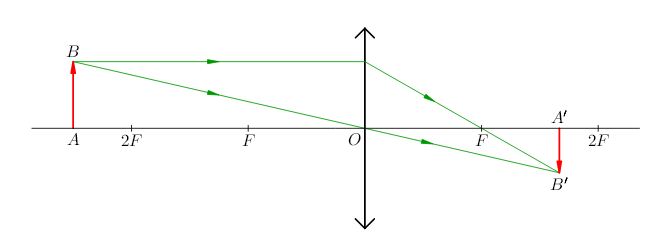Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное

Данная ситуация является обычной для многих оптических приборов: фотоаппаратов, биноклей, телескопов - словом, тех, в которых получают изображения удалённых объектов. По мере удаления предмета от линзы его изображение уменьшается в размерах и приближается к фокальной плоскости.

Рассмотрение первого случая $a>2f$ нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным.

к оглавлению ▴

Собирающая линза: мнимое изображение точки.

Второй случай: $a<f$ . Точечный источник света $S$ расположен между линзой и фокальной плоскостью (рис. 7).

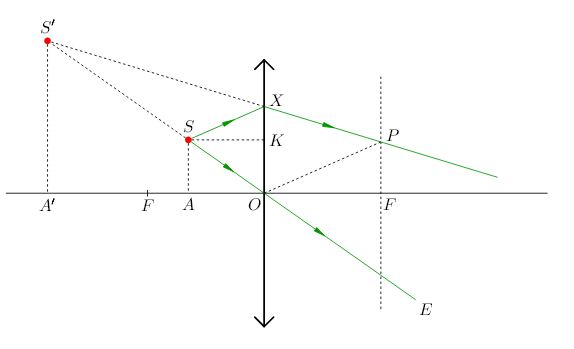Рис. 7. Случай a < f: мнимое изображение точки

Наряду с лучом $SO$ , идущим без преломления, мы снова рассматриваем произвольный луч $SX$ . Однако теперь на выходе из линзы получаются два расходящихся луча $OE$ и $XP$ . Наш глаз продолжит эти лучи до пересечения в точке $S{}$ .

Теорема об изображении утверждает, что точка $S{}$ будет одной и той же для всех лучей $SX$ , исходящих из точки $S$ . Мы опять докажем это с помощью трёх пар подобных треугольников:

$\triangle SAO\sim \triangle S{}$

Снова обозначая через $b$ расстояние от $S{}$ до линзы, имеем соответствующую цепочку равенств (вы уже без труда в ней разберётесь):

$\frac{\displaystyle a}{\displaystyle b}=\frac{\displaystyle AO}{\displaystyle A{}$ . (9)

Отсюда

$b=\frac{\displaystyle fa}{\displaystyle f-\displaystyle a}$ . (10)

Величина $b$ не зависит от луча $SX$ , что и доказывает теорему об изображении для нашего случая $a<f$ . Итак, $S{}$ - мнимое изображение источника $S$ . Если точка $S$ не лежит на главной оптической оси, то для построения изображения $S{}$ удобнее всего брать луч, идущий через оптический центр, и луч, параллельный главной оптической оси (рис. 8).

Рис. 8. Построение изображения точки S, не лежащей на главной оптической оси

Ну а если точка $S$ лежит на главной оптической оси, то деваться некуда - придётся довольствоваться лучом, падающим на линзу наклонно (рис. 9).

Рис. 9. Построение изображения точки S, лежащей на главной оптической оси

Соотношение (9) приводит нас к варианту формулы линзы для рассматриваемого случая $a<f$ . Сначала переписываем это соотношение в виде:

$1-\frac{\displaystyle a}{\displaystyle b}=\frac{\displaystyle a}{\displaystyle f}$ ,

а затем делим обе части полученного равенства на a:

$\frac{\displaystyle 1}{\displaystyle a}-\frac{\displaystyle 1}{\displaystyle b}=\frac{\displaystyle 1}{\displaystyle f}$ . (11)

Сравнивая (7) и (11), мы видим небольшую разницу: перед слагаемым $1/b$ стоит знак плюс, если изображение действительное, и знак минус, если изображение мнимое.

Величина $b$ , вычисляемая по формуле (10), не зависит также от расстояния $SA$ между точкой $S$ и главной оптической осью. Как и выше (вспомните рассуждение с точкой $M$ ), это означает, что изображением отрезка $SA$ на рис. 9 будет отрезок $S{}$ .

к оглавлению ▴

Собирающая линза: мнимое изображение предмета.

Учитывая это, мы легко строим изображение предмета, находящегося между линзой и фокальной плоскостью (рис. 10). Оно получается мнимым, прямым и увеличенным.

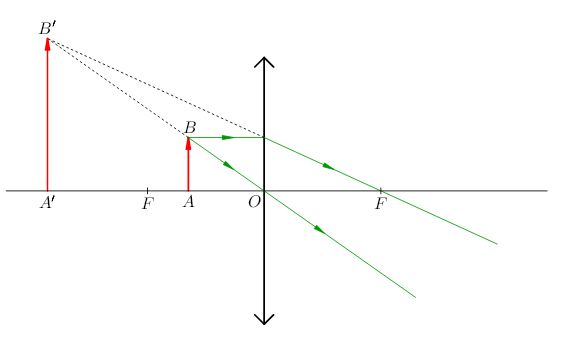Рис. 10. $a<f$ : изображение мнимое, прямое, увеличенное

Такое изображение вы наблюдаете, когда разглядываете мелкий предмет в увеличительное стекло - лупу. Случай $a<f$ полностью разобран. Как видите, он качественно отличается от нашего первого случая $a>f$ . Это не удивительно - ведь между ними лежит промежуточный "катастрофический" случай $a=f$ .

к оглавлению ▴

Собирающая линза: предмет в фокальной плоскости.

Промежуточный случай: $a=f$ . Источник света $S$ расположен в фокальной плоскости линзы (рис. 11).

Как мы помним из предыдущего раздела, лучи параллельного пучка после преломления в собирающей линзе пересекутся в фокальной плоскости - а именно, в главном фокусе, если пучок падает перпендикулярно линзе, и в побочном фокусе при наклонном падении пучка. Воспользовавшись обратимостью хода лучей, мы заключаем, что все лучи источника $S$ , расположенного в фокальной плоскости, после выхода из линзы пойдут параллельно друг другу.

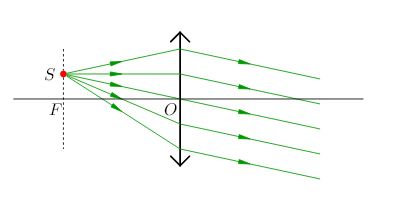Рис. 11. a=f: изображение отсутствует

Где же изображение точки $S$ ? Изображения нет. Впрочем, никто не запрещает нам считать, что параллельные лучи пересекаются в бесконечно удалённой точке. Тогда теорема об изображении сохраняет свою силу и в данном случае - изображение $S{}$ находится на бесконечности.

Соответственно, если предмет целиком расположен в фокальной плоскости, изображение этого предмета будет находиться на бесконечности (или, что то же самое, будет отсутствовать).

Итак, мы полностью рассмотрели построение изображений в собирающей линзе.

к оглавлению ▴

Рассеивающая линза: мнимое изображение точки.

К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.

Снова берём луч $SO$ и произвольный луч $SX$ (рис. 12). На выходе из линзы имеем два расходящихся луча $OE$ и $XY$ , которые наш глаз достраивает до пересечения в точке $S{}$ .

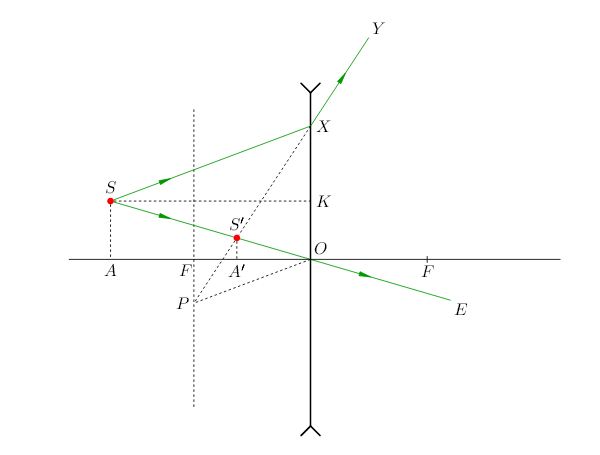Рис. 12. Мнимое изображение точки S в рассеивающей линзе

Нам снова предстоит доказать теорему об изображении - о том, что точка $S{}$ будет одной и той же для всех лучей $SX$ . Действуем с помощью всё тех же трёх пар подобных треугольников:

$\triangle SAO\sim \triangle S{}$ .

Имеем:

$\frac{\displaystyle a}{\displaystyle b}= \frac{\displaystyle AO}{\displaystyle A{}$ (12)

Отсюда

$b=\frac{\displaystyle af}{\displaystyle a+\displaystyle f}$ . (13)

Величина b не зависит от луча span
$SX$ , поэтому продолжения всех преломлённых лучей span
$XY$ пересекутся в точке $S{}$ - мнимом изображении точки $S$ . Теорема об изображении тем самым полностью доказана.

Вспомним, что для собирающей линзы мы получили аналогичные формулы (6) и (10). В случае $a=f$ их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации $a>f$ и $a<f$ .

А вот у формулы (13) знаменатель не обращается в нуль ни при каком a. Стало быть, для рассеивающей линзы не существует качественно разных ситуаций расположения источника - случай тут, как мы и сказали выше, имеется только один.

Если точка $S$ не лежит на главной оптической оси, то для построения её изображения удобны два луча: один идёт через оптический центр, другой - параллельно главной оптической оси (рис. 13).

Рис. 13. Построение изображения точки S, не лежащей на главной оптической оси

Если же точка $S$ лежит на главной оптической оси, то второй луч приходится брать произвольным (рис. 14).

Рис. 14. Построение изображения точки S, лежащей на главной оптической оси

Соотношение (13) даёт нам ещё один вариант формулы линзы. Сначала перепишем:

$1-\frac{\displaystyle a}{\displaystyle b}=-\frac{\displaystyle a}{\displaystyle f}$ ,

а потом разделим обе части полученного равенства на a:

$\frac{\displaystyle 1}{\displaystyle a}-\frac{\displaystyle 1}{\displaystyle b}=-\frac{\displaystyle 1}{\displaystyle f}.$ (14)

Так выглядит формула линзы для рассеивающей линзы.

Три формулы линзы (7), (11) и (14) можно записать единообразно:

$\frac{\displaystyle 1}{\displaystyle a}+\frac{\displaystyle 1}{\displaystyle b}=\frac{\displaystyle 1}{\displaystyle f},$

если соблюдать следующую договорённость о знаках:

- для мнимого изображения величина $b$ считается отрицательной;
- для рассеивающей линзы величина $f$ считается отрицательной.

Это очень удобно и охватывает все рассмотренные случаи.

к оглавлению ▴

Рассеивающая линза: мнимое изображение предмета.

Величина $b$ , вычисляемая по формуле (13), опять-таки не зависит от расстояния $SA$ между точкой $S$ и главной оптической осью. Это снова даёт нам возможность построить изображение предмета $AB$ , которое на сей раз получается мнимым, прямым и уменьшенным (рис. 15).

Рис. 15. Изображение мнимое, прямое, уменьшенное

Разберем задачи ЕГЭ по теме: Тонкие линзы. Построение изображений.

1. Тонкая собирающая линза с фокусным расстоянием F находится между двумя точечными источниками света на расстоянии d=15 см от одного из них. Источники расположены на главной оптической оси на расстоянии L=22,5 см друг от друга. Найдите фокусное расстояние линзы, если их изображения получились в одной точке. Ответ выразите в сантиметрах.
Дано:
$d_1$ = 15 см = 0,15 м
$L$ = 22,5 см=0,225 м
Найти:
Фокусное расстояние F - ?

Решение:
Тонкая собирающая линза дает различные виды изображений: увеличенные (уменьшенные), прямые (обратные), действительные (мнимые). Характеристика изображения зависит от расстояния от предмета до линзы, т.е. от соотношения d и F.
Так как в задаче говорится о получении изображений в одной точке, то один из точечных источников должен находиться за фокусом линзы – он дает действительное изображение. Второй точечный источник должен находиться перед фокусом – он дает мнимое изображение.

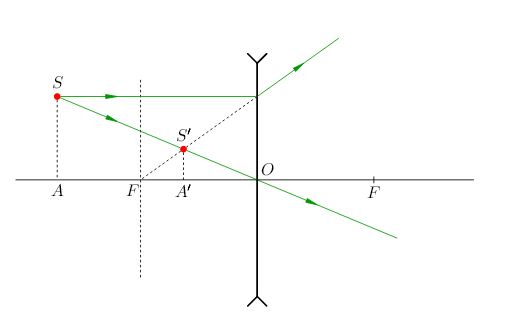
На рис. 1 представлено получение изображения для точечного источника света $S_1$ , находящегося на расстоянии больше фокусного, $S_1$ - изображение точечного источника света $S_1$ .

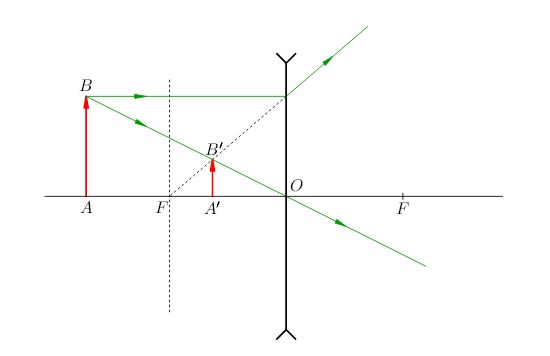
На рис. 2 представлено получение изображения для точечного источника света $S_2$ , находящегося на расстоянии меньше фокусного, $S_2$ - изображение точечного источника света $S_2$ .
После создания модели, поясняющей условие этой задачи, можно переходить к её решению. Для этого надо применить формулу тонкой линзы для двух случаев. С учетом правила знаков $f_1>0,f_2<0$ , так как изображение в первом случае действительное, во втором – мнимое.

$\frac{1}{d_1}+\frac{1}{f_1}=\frac{1}{F} (1)$

$\frac{1}{d_2}-\frac{1}{f_2}=\frac{1}{F} (2)$

Сложим эти два уравнения и учтем, что $\frac{1}{f_1}+\left(-\frac{1}{f_2}\right)=0.$ Так как изображения в двух случаях получались в одной точке, то $f_1=f_2.$

$\frac{1}{d_1}+\frac{1}{d_2}=\frac{2}{F}$

$\frac{d_1+d_2}{d_1\cdot d_2}=\frac{2}{F}$

$F=\frac{2d_1\cdot d_2}{d_1+d_2}$

Определим, что $d_2=L-d_1; d_2=0,225-0,15=0,075$ (м).

$F=\frac{2\cdot 0,15\cdot 0,075}{0,15+0,075}=0,1$ (м) $=10$ (см).

Ответ: 10

2. Какая из точек (1, 2, 3 или 4) является изображением точки S, созданным тонкой собирающей линзой с фокусным расстоянием F (см. рисунок)?

Решение:

Для получения изображения точечного источника S необходимо осуществить построение двух любых лучей, исходящих от этого источника. Самым «удобным» лучом является луч, проходящий через оптический центр линзы. Такие лучи, после прохождения через линзу, не меняют своего направления. На рисунке таким лучом является луч 1-1ʹ.
Второй и третий лучи от точечного источника S попадают на линзу произвольно. Дальнейший ход таких лучей определяется следующим алгоритмом:

необходимо построить побочные оптические оси, параллельные падающим лучам (на рисунке они проведены пунктирной линией);
провести фокальную плоскость и найти точки пересечения этой плоскости с побочными оптическими осями;
продолжить ход световых лучей после прохождения через линзу (на рисунке это лучи 2ʹ и 3ʹ).

Поэтому изображением точечного источника S (точки S) будет являться точка 2.
При решении этой задачи мы рассмотрели ход трех лучей сквозь линзу, для получения ответа достаточно взять любую комбинацию лучей (1-1ʹ и 2 - 2ʹ) или (1-1ʹ и 3 - 3ʹ ).
Ответ: 2

3. Спираль лампочки расположена вблизи главной оптической оси тонкой рассеивающей линзы на расстоянии а от неё перпендикулярно этой оси, причем $F < a < 2F$ , где F – модуль фокусного расстояния линзы. Затем рассеивающую линзу заменили на собирающую с фокусным расстоянием F. Установите соответствие между видом линзы, использованной в опыте, и свойствами даваемого ею изображения.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Виды линз	Свойства изображения
А) линза рассеивающая	1) мнимое, прямое, уменьшенное
Б) линза собирающая	2) мнимое, перевёрнутое, увеличенное
	3) действительное, перевёрнутое, увеличенное
	4) действительное, прямое, увеличенное

Решение
Решение подобных задач опирается на умение строить изображения протяженных (имеющих размеры) предметов при прохождении лучей через линзу.

Рис.1

На рис.1 выполнено построение изображения предмета АВ в тонкой собирающей линзе. Для этого применялись следующие лучи:
1-1ʹ - луч, проходящий через оптический центр, не преломляется;
2 - 2ʹ - луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный за линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
увеличенное (размер изображения превышает размер предмета),
перевернутое (направления стрелок АВ и АʹВʹ противоположны),
действительное (предмет и его изображения находятся по разные стороны от линзы).

Рис.2

На рис.2 выполнено построение изображения предмета АВ в тонкой рассеивающей линзе. Для этого применялись следующие лучи:
1-1ʹ - луч, проходящий через оптический центр, не преломляется;
2 - 2ʹ - луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный перед линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
уменьшенное (размер изображения меньше размера предмета),
прямое (направления стрелок АВ и АʹВʹ совпадают),
мнимое (предмет и его изображения находятся с одной стороны от линзы).
Полученные изображения и их характеристики приводят к следующему ответу:

А	Б
1	3

4. На рисунке показан ход лучей от точечного источника света S через тонкую линзу. Какова оптическая сила этой линзы? (Ответ дать в диоптриях.)

Решение:

На рисунке представлен ход световых лучей от точечного источника света S. Луч, проходящий через оптический центр, не меняет своего направления. Второй луч, идущий параллельно главной оптической оси, после преломления идет через фокус. Это позволяет определить фокусное расстояние линзы. Согласно рисунку, оно равно двум клеткам. С учётом указанного масштаба, длина одной клетки равна 4 см. Таким образом, фокусное расстояние этой линзы F=8 см = 0,08 м.

Так как оптическая сила линзы $D=\frac{1}{F}=\frac{1}{0,08}=12,5$ (дптр).

Ответ: 12,5

Если вам нравятся наши материалы - записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Тонкие линзы. Построение изображений.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 06.06.2023

Тонкие линзы. Построение изображений.

Собирающая линза: действительное изображение точки.

Собирающая линза: действительное изображение предмета.

Собирающая линза: мнимое изображение точки.

Собирающая линза: мнимое изображение предмета.

Собирающая линза: предмет в фокальной плоскости.

Рассеивающая линза: мнимое изображение точки.

Рассеивающая линза: мнимое изображение предмета.

Это полезно