Задача №17. Построение запросов для поисковых систем. Расположение запросов по возрастанию (убыванию). Подсчет количества страниц.

Для быстрого поиска информации в Интернете используют поисковые запросы. Поисковый запрос – это набор ключевых слов, соединенных знаками логических операций И, ИЛИ, НЕ.

Приоритет выполнения операций, если нет специально поставленных скобок, следующий: сначала НЕ, затем И, затем ИЛИ.

Нужно понимать, что операция И (одновременное выполнение условий) сокращает объем получаемого результата, а операция ИЛИ (выполнение хотя бы одного из условий) наоборот увеличивает объем.

Если в запросе стоит фраза в кавычках, система будет искать точно такую фразу целиком.

1. Расположение запросов по возрастанию (убыванию)

Операция «И» (&) обозначает одновременное присутствие ключевых слов в искомых документах, а потому уменьшает количество найденной информации. Чем больше ключевых слов соединены операцией «И», тем меньше количество найденной информации. И наоборот, операция «ИЛИ» (|) обозначает присутствие хотя бы одного ключевого слова в искомых документах, а потому увеличивает количество найденной информации.

Пример 1.

В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

А) реферат | математика | Гаусс
Б) реферат | математика | Гаусс | метод
В) реферат | математика
Г) реферат & математика & Гаусс

Решение:

Самое маленькое количество страниц будет отобрано по запросу с наибольшим количеством операций «И» (запрос Г), Самое большое количество страниц будет отобрано по запросу с наибольшим количеством операций «ИЛИ» (запрос Б). По запросу А будет отобрано больше страниц, чем по запросу В, т.к. запрос А содержит больше ключевых слов, связанных операцией «ИЛИ».

Ответ: ГВАБ

2. Подсчет найденных по запросу страниц

Такой тип задач обычно решают системой уравнений. Предложу более наглядный и простой способ.

Принцип отбора информации по поисковым запросам хорошо иллюстрирует диаграмма Эйлера-Венна (круги Эйлера). На диаграмме множества изображаются пересекающимися кругами. Операция «И» (&) - это пересечение кругов, а операция «ИЛИ» (|) – это объединение кругов.

Например, обозначим кругами множества Яблоки, Груши, Бананы. По запросу Яблоки & Груши & Бананы будет отобрано пересечение (общая часть) всех трех кругов:

По запросу Яблоки | Груши будет отобрано объединение двух кругов:

Пример 2.

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

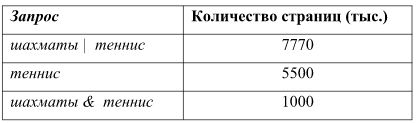
Сколько страниц (в тысячах) будет найдено по запросу шахматы?

Решение:

Нарисуем диаграмму Эйлера-Венна. Прием решения задачи состоит в подсчете количества страниц, соответствующего каждой области, ограниченной линиями:

Запросу шахматы & теннис соответствует средняя область (1000 тыс. страниц), а запросу теннис – весь правый круг (5500 тыс. страниц).

Тогда правый «обрезанный круг» - это 5500-1000=4500:

Запросу шахматы | теннис соответствуют оба круга (7770), тогда левый «обрезанный круг» - это 7770-5500=2270

Итак, мы посчитали количества страниц для каждой ограниченной линиями области:

Несложно увидеть, что по запросу шахматы будет найдено 2270+1000=3270 тыс. страниц.

Ответ: 3270

Пример 3.

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Сколько страниц (в тысячах) будет найдено по запросу

Москва & (Париж | Лондон)

Решение:

Как и в предыдущей задаче, нарисуем диаграмму Эйлера-Венна и посчитаем количество страниц, соответствующее каждой известной области, ограниченной линиями:

Несложно увидеть, что запросу Москва & (Париж | Лондон) соответствует область:

Ответ: 427