Параллелограмм и его свойства

Параллелограмм – это четырехугольник, имеющий две пары параллельных сторон.

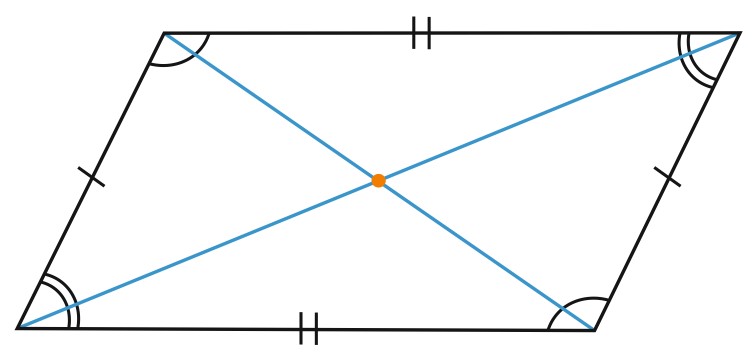
Свойства параллелограмма:

1) Противоположные стороны параллелограмма равны.

2) Противоположные углы параллелограмма равны.

3) Диагонали параллелограмма в точке пересечения делятся пополам.

4) Сумма углов, прилежащих к одной стороне параллелограмма, равна 180 градусов.

1. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.

Решение:

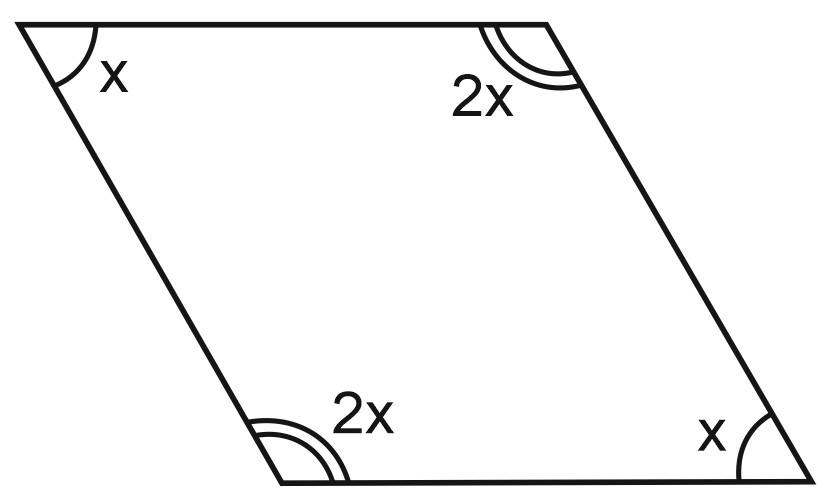
Пусть один из углов равен \(x\), тогда второй равен \(2x\). Противоположные углы параллелограмма равны. Напротив угла \(x\) расположен такой же угол \(x\), а напротив угла \(2x\) – равный ему.

Сумма углов этого параллелограмма равна \(x+x+2x+2x=6x=360\) градусов.

Отсюда \(x\) равен \(60\) градусов. Это меньший угол параллелограмма.

Ответ: 60.

Признак параллелограмма

Как узнать, что четырехугольник является параллелограммом? Для этого применяется признак параллелограмма.

Если две стороны четырехугольника параллельны и равны друг другу, то такой четырехугольник – параллелограмм.

Докажем это. Пусть \(ABCD\) – четырехугольник, в которой \(AB\) параллельна и равна \(CD\).

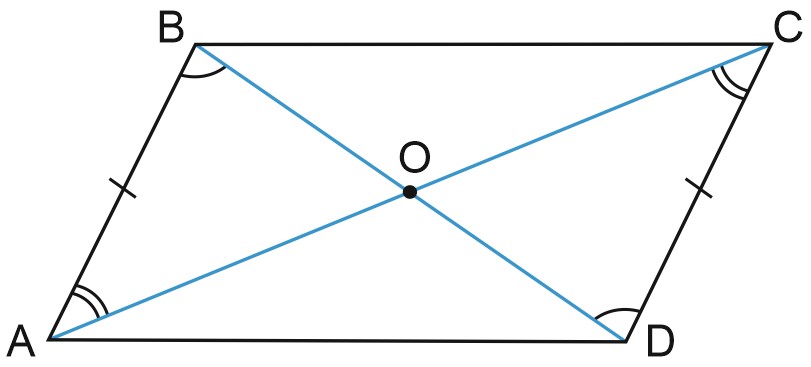
Углы \(BAC\) и \(ACD\) равны как накрест лежащие. Аналогично, угол \(ABD\) равен углу \(BDC\). Мы получили, что треугольники \(AOB\) и \(COD\) равны по стороне и двум углам.

Тогда \(OC=OA, \; OB=OD,\) углы \(BOC\) и \(AOD\) равны как вертикальные. Это значит, что \(BC=AD\), а также углы \(CAD\) и \(ACB\) равны (лежат напротив равных сторон в равных треугольниках). Эти углы – накрест лежащие, поэтому \(AD\) параллельна \(BC\), у нашего четырехугольника 2 пары параллельных сторон.

Мы доказали признак параллелограмма.

2. Диагональ \(AC\) параллелограмма \(ABCD\) образует с его сторонами углы, равные \(30{}^\circ\) и \(45{}^\circ.\) Найдите больший угол параллелограмма. Ответ дайте в градусах.

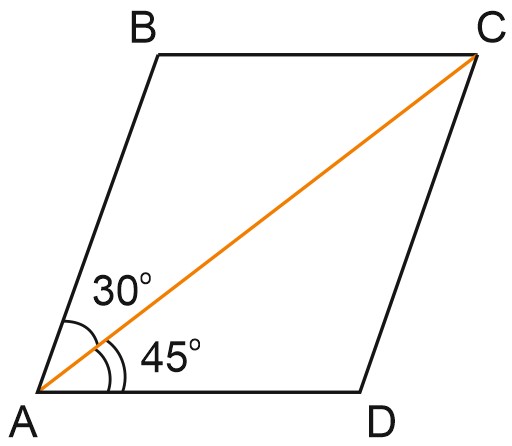
Решение:

\(\angle A=\angle BAC+\angle CAD=30{}^\circ +45{}^\circ =75{}^\circ ,\)

\(\angle A\) и \(\angle B\) – внутренние односторонние углы при параллельных прямых.

\(AD\parallel BC\) и секущей \(AB\), их сумма равна \(180{}^\circ .\)

Тогда \(\angle B=180{}^\circ -\angle A=180{}^\circ -75{}^\circ =105{}^\circ .\)

Это наибольший угол параллелограмма.

Ответ: 105.

3. Найдите величину тупого угла параллелограмма \(ABCD\), если биссектриса угла \(A\) образует со стороной \(BC\) угол, равный \(15{}^\circ.\) Ответ дайте в градусах.

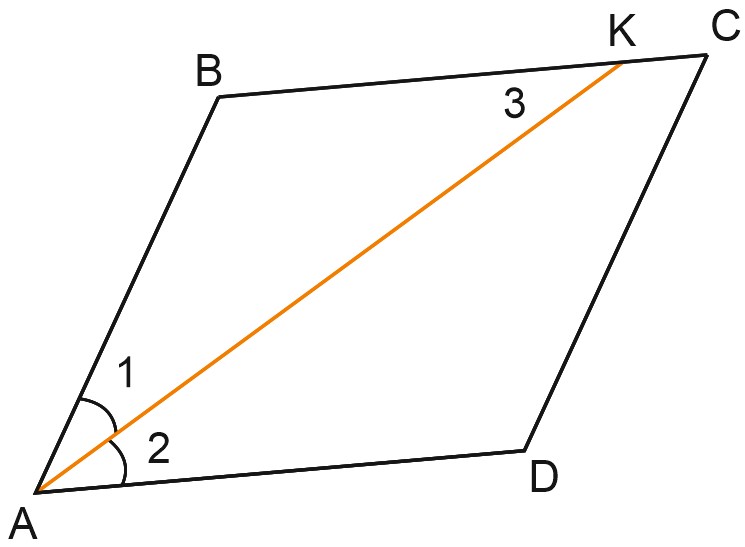
Решение:

\(AK\) – биссектриса угла \(A\) параллелограмма \(ABCD, \; \angle A=30{}^\circ. \)

\(\angle A\) и \(\angle B\) – внутренние односторонние углы при параллельных прямых.

\(AD\parallel BC\) и секущей \(AB\). Их сумма равна \(180{}^\circ ,\) значит, \(\angle B=180{}^\circ -30{}^\circ =150{}^\circ. \)

Ответ: 150.

4. В параллелограмме \(ABCD\) диагональ \(AC\) в 2 раза больше стороны \(AB\) и \(\angle ACD=169{}^\circ .\) Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.

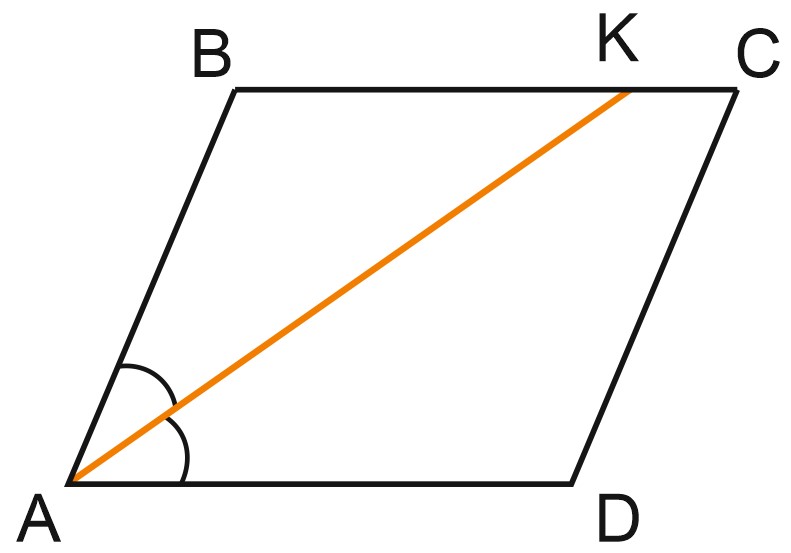
Решение:

\(AC=2AB\Rightarrow AO=OC=AB=CD,\) тогда \(\triangle COD\) – равнобедренный, в нем \(OC=CD.\)

Значит, \(\angle COD=\angle CDO=\displaystyle \frac{180{}^\circ -169{}^\circ }{2}=5,5{}^\circ .\)

Ответ: 5,5.

Биссектрисы углов параллелограмма, прилежащих к одной стороне, – перпендикулярны.

Доказательство:

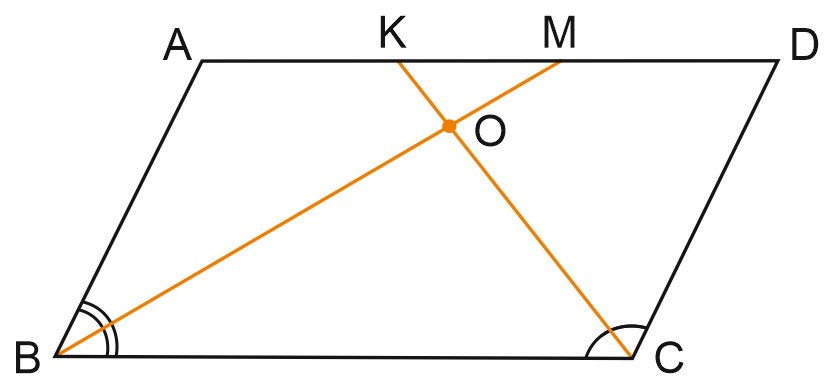
Пусть \(BM\) и \(CK\) – биссектрисы углов параллелограмма, прилежащих к стороне \(BC\).

Сумма углов \(ABC\) и \(BCD\) равна \(180^{\circ}\).

Углы \(OBC\) и \(OCB\) – половинки углов \(ABC\) и \(BCD\). Значит, сумма углов \(ABC\) и \(BCD\) равна \(90\) градусов.

Из треугольника \(BOC\) находим, что угол \(BOC\) – прямой.

Ответ: \(90\).

Мы только что доказали теорему.

Биссектрисы углов параллелограмма, прилежащих к одной стороне, – перпендикулярны.

Легко доказывается и другая теорема:

Биссектрисы противоположных углов параллелограмма – параллельны.

Доказательство:

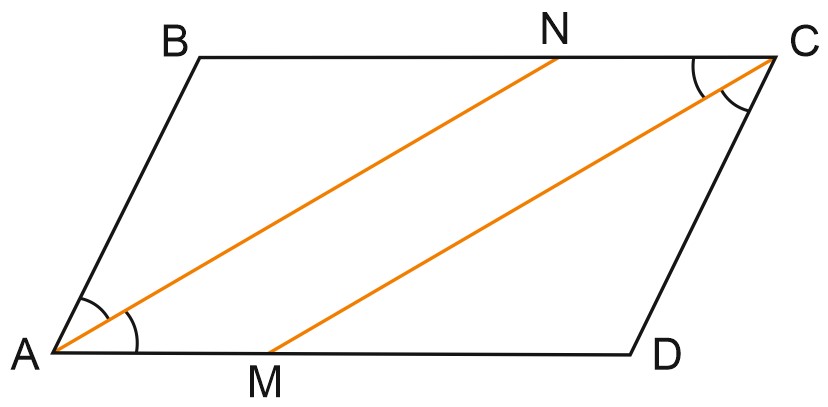
Пусть \(AN\) и \(CM\) – биссектрисы противоположных углов параллелограмма.

Тогда \(\angle BAN=\angle NAM=\displaystyle \frac{1}{2}\angle A; \; \angle BCM=\angle MCD=\displaystyle \frac{1}{2}\angle D.\)

\(\angle A=\angle D,\) так как противоположные углы параллелограмма равны.

Отсюда \(\angle NAM=\angle BCM.\)

С другой стороны, \(\angle NAM=\angle ANB\) как накрест лежащие.

Значит, \(\angle BCM=\angle ANB.\)

Эти углы – соответственные при прямых \(AN\) и \(CM.\)

Соответственные углы равны, следовательно, \(AN\parallel CM.\)

И еще одно интересное свойство параллелограмма.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Доказательство:

Пусть \(AK\) – биссектриса угла \(A\) параллелограмма \(ABCD\). Тогда углы \(BAK\) и \(DAK\) равны.

Также угол \(DAK\) равен углу \(AKB\) как накрест лежащие. Значит, треугольник \(ABK\) равнобедренный.

5. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна \(5\). Найдите его большую сторону.

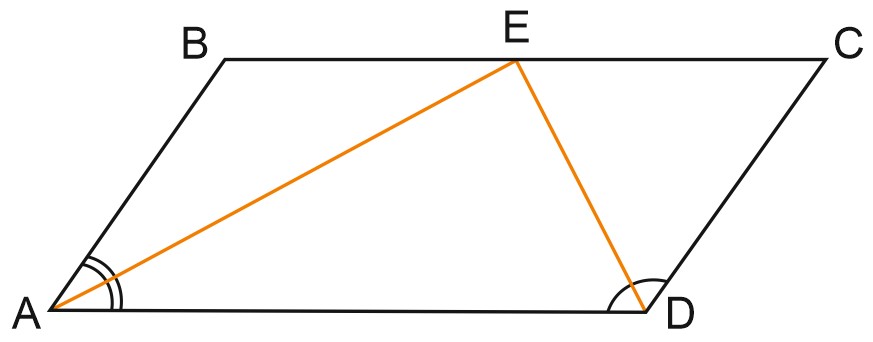
Решение:

Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.

Углы \(DAE\) и \(BEA\), а также \(CED\) и \(ADE\) – накрест лежащие. Накрест лежащие углы равны. Значит, угол \(DAE\) равен углу \(BEA\), а угол \(CED\) — углу \(ADE\).

Получаем, что треугольники \(ABE\) и \(CDE\) – равнобедренные, то есть \(BE=AB\), а \(EC=CD.\)

Тогда \(BC = 5+5=10.\)

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

6. Биссектрисы углов \(A\) и \(B\) параллелограмма \(ABCD\) пересекаются в точке \(K\). Найдите площадь параллелограмма, если \(BC=7\), а расстояние от точки \(K\) до стороны \(AB\) равно \(4\).

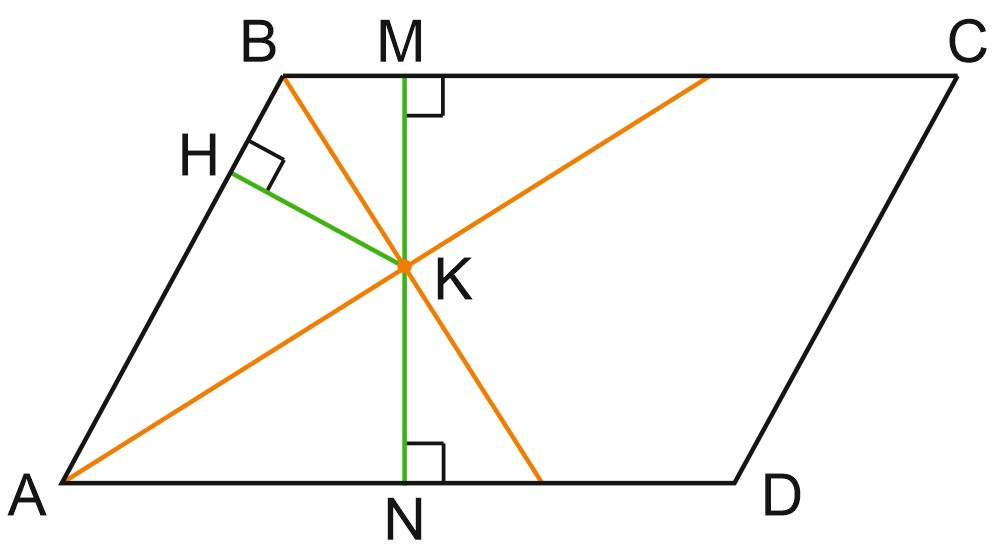
Решение:

Биссектрисы углов параллелограмма, прилежащих к одной стороне, – перпендикулярны.

Значит, треугольник \(AKB\) – прямоугольный.

Расстояние от точки \(K\) до стороны \(AB\) – это длина перпендикуляра, проведенного из точки \(K\) на прямую \(AB\), т. е. \(KH=4.\)

\(\triangle AKN=\triangle AKH\) по гипотенузе и острому углу \(\Rightarrow KN=KH.\)

Аналогично, \(\triangle BKH=\triangle BKM\) по гипотенузе и острому углу \(\Rightarrow KH=KM.\)

\(KN=KH=KM=4\Rightarrow MN=8.\)

Тогда \(S_{ABCD}=AD\cdot MN; \; S_{ABCD}=8\cdot 7=56.\)

Ответ: 56.

7. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении \(3:4,\) считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен \(88\).

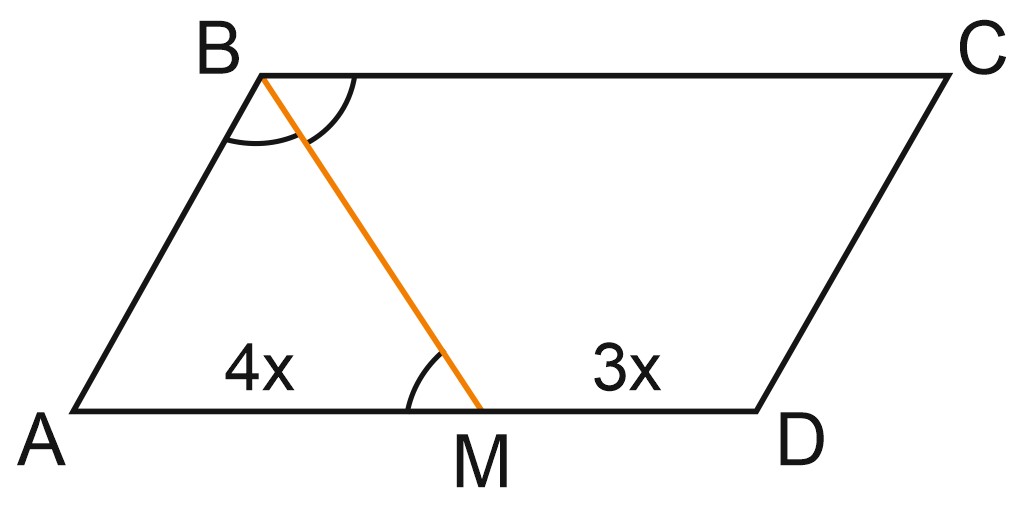
Решение:

Напомним, что биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Пусть \(BM\) – биссектриса тупого угла \(B\). По условию, отрезки \(MD\) и \(AB\) равны \(3x\) и \(4x\) соответственно.

Рассмотрим углы \(CBM\) и \(BMA\). Поскольку \(AD\) и \(BC\) параллельны, \(BM\) – секущая, углы \(CBM\) и \(BMA\) являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник \(ABM\) – равнобедренный, следовательно, \(AB = AM = 4x.\)

Периметр параллелограмма – это сумма всех его сторон, то есть

\(7x+7x+4x+4x=88.\)

Отсюда \(x=4, \; 7x=28.\)

Ответ: 28.

8. В параллелограмме \(ABCD\) проведена биссектриса угла \(A\), пересекающая сторону \(BC\) в точке \(K\). Найдите \(KC,\) если \(AB=4\), а периметр параллелограмма равен \(20\).

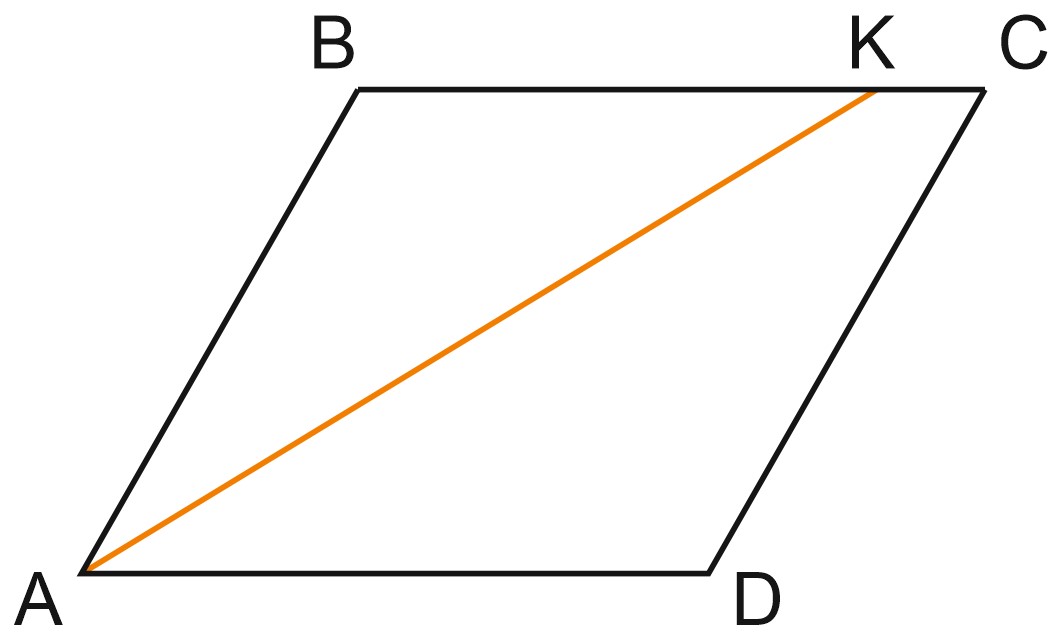
Решение:

\(ABCD\) – параллелограмм, тогда \(AB = DC = 4.\)

\(AK\) – биссектриса угла \(A\), значит, \(\angle BAK=\angle KAD;\)

\(\angle KAD=\angle AKC\) как накрест лежащие углы при параллельных прямых \(BC\) и \(AD\) и секущей \(AK\).

Получили, что \(\triangle ABK\) – равнобедренный и \(AB=BK=4.\)

\(P_{ABCD}=\left(AB+AD\right)\cdot 2=20,\) значит \(AB+AD=10\Rightarrow AD=6,\)

\(KC=BC-BK=6-4=2.\)

Ответ: 2.

Запишем формулы площади параллелограмма:

\(S=a \cdot h\), где \(a\) — основание параллелограмма, \(h\) — его высота.

\(S=a \cdot b \cdot \sin \varphi\), где \(a\) и \(b\) — стороны параллелограмма, \(\varphi\) — угол между ними.

На схеме показаны виды параллелограммов. Квадрат обладает и свойствами прямоугольника, и свойствами ромба.

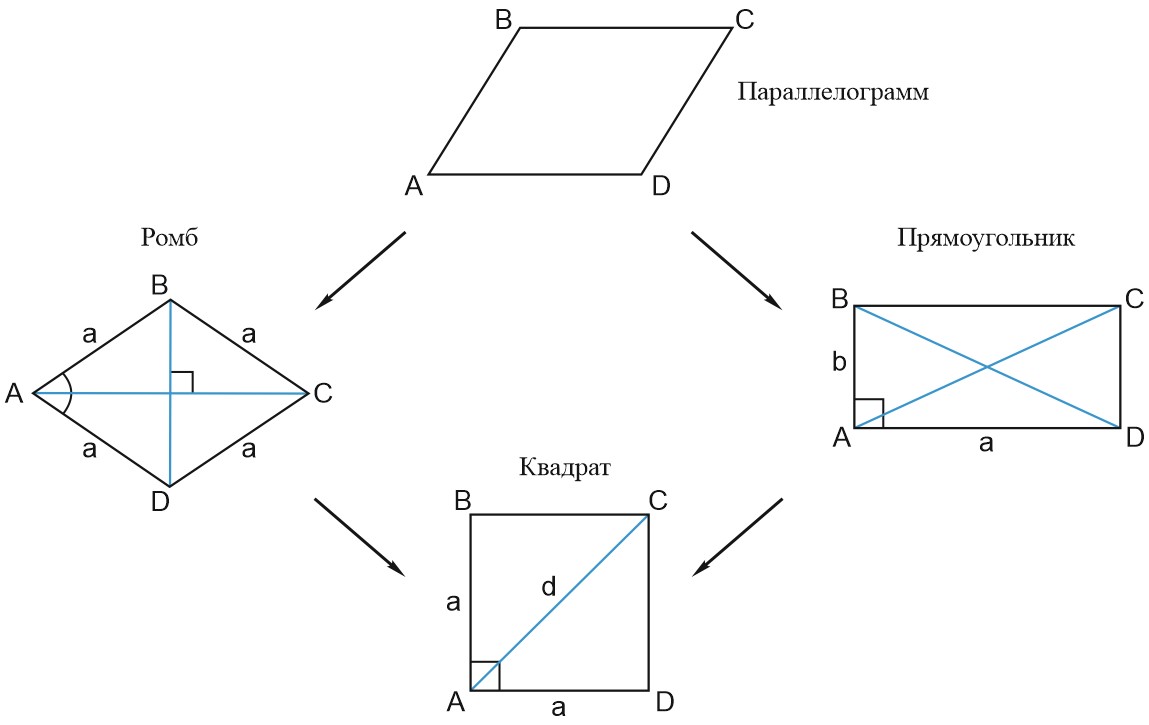
В следующих статьях мы изучим свойства прямоугольника, ромба, квадрата.