Стереометрия на ЕГЭ. Приемы и секреты.
Вы уже знаете, что задачи по стереометрии в первой части ЕГЭ на самом деле простые. Правильный чертеж, элементарная логика, внимательность, плюс некоторые приемы, о которых мы рассказали в первой части статьи и еще расскажем — вот и всё, что вам нужно. Перейдем сразу к практике.
1. Объем параллелограмма равен \(9\). Найдите объем треугольной пирамиды \(AB\mkern -3muD\mkern -3muA_1\).

Решение:
Мы помним, что объем параллелепипеда равен \(S_{осн} \cdot h\). А объем пирамиды равен \(\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 3}S_{осн} \cdot h\).
Иными словами, если у параллелепипеда и пирамиды одинаковые основания и одинаковые высоты, то объем пирамиды будет в три раза меньше, чем объем параллелепипеда. А у нашей пирамиды еще и площадь основания в два раза меньше. Значит, ее объем в шесть раз меньше объема параллелепипеда.
Ответ: \(1,5\).
2. Объем куба равен \(12\). Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:
Об одном из способов решения этой задачи мы уже рассказали. Посчитайте, сколько нужно четырехугольных пирамидок, чтобы сложить из них такой кубик.
Есть и второй способ. Если бы пирамида и куб имели одинаковые высоты, объем пирамиды был бы в \(3\) раза меньше объема куба (поскольку площади основания у них одинаковые). А у нашей пирамиды высота в два раза меньше, чем у куба. Значит, ее объем будет в \(6\) раз меньше, чем у куба.
Ответ: \(2\).
3. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Решение:
На самом деле это задача по алгебре, причем элементарная. Объем шара равен \(\genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle 3} \pi R^3\). Осталось решить уравнение:
\(\genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle 3} \pi 6^3+\genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle 3} \pi 8^3+\genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle 3} \pi 10^3=\genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle 3} \pi R^3;\)
\(6^3+8^3+10^3=R^3;\)
\(R^3=1728.\)
Как извлечь кубический корень из этого числа? Очень просто — разложите его на множители.
\(1728=8 \cdot 216=2^3 \cdot 6^3;\)
\(R=2 \cdot 6 = 12.\)
Ответ: \(12\).
4. Найдите высоту правильной треугольной пирамиды, стороны которой равны \(2\), а объем равен \(\sqrt{3}\).

Решение:
Мы говорили, что в основании правильной треугольной пирамиды лежит правильный треугольник. У него все углы равны
\(60^{\circ}\) и все стороны тоже равны. Площадь его проще всего найти по формуле
\(S=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}a^2 \sin 60^{\circ}\). Она равна \(\sqrt{3}\). Поскольку
\(V=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 3}Sh\), высота равна \(3\).
Ответ: \(3\).
5. Найдите \(V\) конуса, образующая которого равна \(2\) и наклонена к плоскости основания под углом \(30\) градусов. В ответе укажите \(\displaystyle\frac{V}{\pi }\).

Решение:
Если вы вдруг забыли, что такое образующая, — смотрите нашу таблицу с формулами. А что значит «наклонена к плоскости основания»? Вспомним, что угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость, то есть угол \(O\mkern -3muAS\).
Из прямоугольного треугольника \(AO\mkern -3muS\) находим, что \(O\mkern -3muS=h=1, \; AO=R=\sqrt{3}\).
Объем конуса найдем по известной формуле и поделим на \(\pi\).
Ответ: \(1\).
6. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами \(2\), а боковые ребра равны \(2\sqrt{3}\) и наклонены к плоскости основания под углом \(30\) градусов.

Решение:
Нарисуйте вид сверху, то есть правильный шестиугольник. У него все стороны равны, все углы тоже равны.

Как найти площадь правильного шестиугольника, если специальную формулу вы не знаете? Проще всего разбить его на \(6\) одинаковых равносторонних треугольников.
Формула площади равностороннего треугольника вам известна: \(S=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}a^2 \sin 60^{\circ}.\)
Итак, площадь основания равна \(6\sqrt{3}\). Осталось найти высоту.
Высота призмы — это отрезок, перпендикулярный ее основаниям. Из прямоугольного треугольника \(ACH\) находим:
\(h=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}AC=\sqrt{3}.\)
Ответ: \(18\).
7. Диагональ прямоугольного параллелепипеда равна \(\sqrt{2}\) и образует углы \(30, \; 30\) и \(45\) градусов с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Решение:
Мы уже говорили, что угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Обозначим вершины параллелепипеда.

Проекцией диагонали \(B\mkern -3muD_1\) на нижнее основание будет отрезок \(B\mkern -3muD\).
Пусть диагональ образует угол \(45\) градусов именно с плоскостью нижнего основания.
Рассмотрим прямоугольный треугольник \(B\mkern -3muD \mkern -3muD_1\).
По теореме Пифагора, \(D\mkern -3muD_1=B\mkern -3muD_1 \cdot \sin 45^{\circ}=1\). Итак, мы нашли высоту параллелепипеда.
Проекцией \(B\mkern -3muD_1\) на переднюю грань будет отрезок \(A_1B\).
Из прямоугольного треугольника \(A_1B\mkern -3muD_1\) найдем \(A_1\mkern -3muD_1=B\mkern -3muD_1 \cdot \sin 30^{\circ}=\genfrac{}{}{}{0}{\displaystyle \sqrt{2}}{\displaystyle 2}\). Мы нашли ширину параллелепипеда.
А его длина (то есть отрезок \(C_1\mkern -3muD_1\)) находится аналогично. Она тоже равна \(\genfrac{}{}{}{0}{\displaystyle \sqrt{2}}{\displaystyle 2}\).
Объем параллелепипеда равен \(\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}\).
Ответ: \(0,5\).
8. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно \(3\). Найдите объем пирамиды.

Решение:
Если решать «в лоб», считая, что \(ABC\) — основание, то у нас получится задача по стереометрии из второй части ЕГЭ. Но зачем такие сложности? Развернем пирамиду.
Объем пирамиды равен \(\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 3}S_{осн}h\). В основании лежит равнобедренный прямоугольный треугольник, площадь которого равна \(4,5\).
Тогда объем пирамиды равен \(4,5\).
Ответ: \(4,5\).
9. Объем треугольной пирамиды \(S\mkern -2muABC\), являющейся частью правильной шестиугольной пирамиды \(S\mkern -2muABC\mkern -3muD\mkern -2muE\mkern -2muF\), равен \(1\). Найдите объем шестиугольной пирамиды.

Решение:
У треугольной и шестиугольной пирамид, о которых говорится в условии, одинаковые высоты. Разные только площади основания. Нарисуем вид снизу.

Видим, что площадь основания треугольной пирамиды в \(6\) раз меньше, чем у шестиугольной.
Ответ: \(6\).
Если в условии задачи по стереометрии дан рисунок — значит, повезло. Рисунок — это уже половина решения. А если его нет? Значит, рисуйте сами, как умеете. Отговорки «не умею» или «рисование у нас было только в детском саду» — не принимаются. Вам ведь не девочку на шаре надо изобразить, а намного более простые объекты :-)
10. Середина ребра куба со стороной \(1,9\) является центром шара радиуса \(0,95\). Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите \(S\).
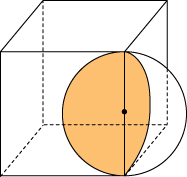
Решение:
Обратите внимание, что \(0,95 \cdot 2=1,9\). Значит, сторона куба является диаметром шара. Осталось понять, какая часть шара лежит внутри куба.
Правильный ответ: \(0,9025\).
Ответ: \(0,9025\).
11. Вершина \(A\) куба \(ABCDA_1B_1C_1D_1\) со стороной \(1,6\) является центром сферы, проходящей через точку \(A_1\). Найдите площадь \(S\) части сферы, содержащейся внутри куба. В ответе запишите величину \(S\).
Решение:
Здесь главное — понять, какая часть шара лежит внутри куба. Порисуйте кубики и шарики. Пока есть возможность, возьмите яблоко (оно почти шарообразной формы), потренируйтесь. Жаль, что на ЕГЭ вам не выдадут килограмма яблок для отработки пространственного мышления.
Правильный ответ: \(1,28\).
Ответ: \(1,28\).
Если вы его не получили, смотрите подсказку в конце статьи.
12. Объем треугольной пирамиды равен \(15\). Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении \(1:2\), считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

Решение:
Прежде всего, что значит «точка делит боковое ребро в отношении \(1:2\), считая от вершины»? Это значит, что она делит его на отрезки, длины которых \(x\) и \(2x\).
Плоскость \(AB\mkern -2muM\) делит пирамиду \(ABC\mkern -2muS\) на две.
У пирамид \(ABC\mkern -2muM\) и \(ABCS\) общее основание \(ABC\). Ясно, что отношение их объемов равно отношению высот.
Проведем перпендикуляры \(SO\) и \(M\mkern -3muH\) к плоскости основания пирамиды.
\(SO\) — высота пирамиды \(ABCS, \; MH\) — высота пирамиды \(ABC\mkern -2muM\).
Очевидно, что отрезок \(SO\) параллелен отрезку \(M\mkern -3muH\), поскольку два перпендикуляра к одной плоскости параллельны друг другу. Через две параллельные прямые можно провести плоскость, причем только одну.
Итак, точки \(M, \; S, \; C, \; O\) и \(H\) лежат в одной плоскости, то есть мы от стереометрической задачи перешли к плоской, планиметрической.

Треугольники \(SOC\) и \(M\mkern -3muH\mkern -3muC\) подобны, \(MC:SC=M\mkern -3muH:SO=2:3\).
Значит, \(M\mkern -3muH=\genfrac{}{}{}{0}{\displaystyle 2}{\displaystyle 3}SO\).
Объем пирамиды \(ABC\mkern -2muM\) равен \(\genfrac{}{}{}{0}{\displaystyle 2}{\displaystyle 3}\) объема пирамиды \(ABC\mkern -2muS\).
Ответ: \(10\).
13. Ребра тетраэдра равны \(1\). Найдите площадь сечения, проходящего через середины четырех его ребер.

Решение:
Прежде всего, все ребра равны, значит, тетраэдр — правильный. В его основании лежит равносторонний треугольник, а вершина проецируется в центр этого треугольника.
Как вы думаете, какая фигура получится в сечении?
Заметим, что отрезок \(K\mkern -3muL\) параллелен \(BS\) поскольку является средней линией треугольника \(AS\mkern -3muB\). И отрезок \(M\mkern -3muN\) тоже параллелен \(BS\), потому что является средней линией треугольника \(BSC\).
Значит, \(K\mkern -3muL\) параллелен \(M\mkern -3muN\).
Аналогично \(LM\) параллелен \(K\mkern -3muN\).
Мы помним, что средняя линия треугольника не только параллельна основанию — она равна половине основания. А у нашего тетраэдра все ребра равны. Значит, \(K\mkern -3muL\mkern -3muM\mkern -3muN\) — ромб, все стороны которого равны \(0,5\). Уже хорошо.
Мы уже сказали, что у правильного тетраэдра вершина (точка \(S\)) проецируется в центр основания (точка \(O\)). В основании — правильный треугольник. Значит, точка \(O\) будет точкой пересечения биссектрис, медиан и высот этого треугольника, и тогда \(O\mkern -3muB\) перпендикулярен \(AC\).
Вспомним теорему о трех перпендикулярах. \(O\mkern -3muB\) является проекцией \(S\mkern -2muB\) на плоскость основания, следовательно, отрезок \(S\mkern -2muB\) тоже перпендикулярен \(AC\). И тогда \(K\mkern -3muL\mkern -3muM\mkern -3muN\) — квадрат.
Его площадь равна \(0,25\).
Ответ: \(0,25\).
А теперь — самые сложные задачи по стереометрии из первой части варианта ЕГЭ. Для их решения существуют секретные приемы. Конечно же, лучше знать их заранее, чем изобретать на экзамене.
14. Объем тетраэдра равен \(1,9\). Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

Решение:
Можно долго искать формулу объема октаэдра (а именно он там и находится, в серединке), а можно поступить умнее.
Помните, как в задаче \(B6\) мы считали площадь неудобно расположенных фигур?

Здесь проще всего посчитать площадь квадрата со стороной \(5\), в который вписан данный треугольник. И вычесть из нее площади трех прямоугольных треугольников. Видите их на рисунке?
В нашей задаче про тетраэдр и многогранник можем поступить аналогично. Как получился этот многогранник в серединке? От исходного тетраэдра отрезали четыре маленьких тетраэдра, объем каждого из которых в \(8\) раз меньше, чем объем большого (об этом мы уже говорили).
Получаем: \(V-\genfrac{}{}{}{0}{\displaystyle 4}{\displaystyle 8}V=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}V\).
Ответ: \(0,95\).
15. Объем параллелепипеда равен \(4,5\). Найдите объем треугольной пирамиды \(AD_1\mkern -2muC\mkern -2muB_1\).

Решение:
Обратите внимание, нарисован куб, а написано — параллелепипед.
Мы знаем, что его объем равен \(4,5\), но не знаем, чему равны его длина, ширина и высота. Обозначим их \(a, \; b\) и \(c\).
Не так-то просто найти площадь основания и высоту пирамиды \(AD_1\mkern -2muC\mkern -2muB_1\). Так может, и не надо этого делать?
Есть более удобный способ — тот же, что и в предыдущей задаче. Ведь пирамида \(AD_1\mkern -2muC\mkern -2muB_1\) получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — \(ABC\mkern -2muB_1\), \(D_1B_1CC_1, \; AA_1D_1B_1\) и \(ADC\mkern -2muD_1\). А объем каждой из них легко посчитать — мы делали это в первой задаче этой статьи.
Например, объем пирамиды \(ABC\mkern -2muB_1\) равен \(\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 6}\) объема параллелепипеда.
Объем четырех всех пирамид, которые отрезали, равен \(\genfrac{}{}{}{0}{\displaystyle 2}{\displaystyle 3}\) объема параллелепипеда.
Значит, объем пирамиды \(AD_1\mkern -2muC\mkern -2muB_1\) равен \(\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 3}\) объема параллелепипеда.
Ответ: \(1,5\).
Поздравляем! Задачи по стереометрии из первой части ЕГЭ по математике освоены — от простых до самых сложных. Заходите чаще на наш сайт.
Подсказка к задаче \(11\):



















































