Сумма углов треугольника

Теорема. Сумма углов треугольника равна \(180\) градусов.

Доказательство:

Нарисуем треугольник. Через одну из его вершин проведем прямую, параллельную противоположной стороне, и найдем на рисунке равные углы.

Угол 1 равен углу \(BAC\), они накрест лежащие. Угол 2 равен углу \(ACB\), они тоже накрест лежащие.

Сумма угла 1, угла \(ABC\) и угла 2 составляет развернутый угол.

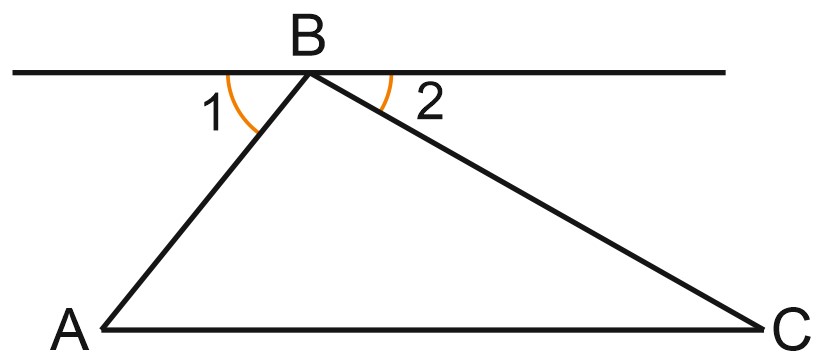
A развернутый угол равен \(180{}^\circ \). Значит, и сумма углов треугольника равна \(180\) градусов. Теорема доказана.

Разберем задачи ЕГЭ и ОГЭ, в которых фигурирует сумма углов треугольника.

1. В треугольнике два угла равны \({57}^\circ\) и \({86}^\circ\). Найдите его третий угол. Ответ дайте в градусах.

Решение:

Сумма углов в треугольнике равна \(180{}^\circ \), поэтому третий угол равен \(180{}^\circ -57{}^\circ -86{}^\circ =37{}^\circ \).

Ответ: 37.

2. Один из острых углов в прямоугольном треугольнике равен \(48{}^\circ \). Найдите его другой острый угол. Ответ дайте в градусах.

Решение:

Покажем все данные на чертеже. Прямой угол можно отмечать специальным знаком, не подписывая \(90{}^\circ \), чтобы не перегружать чертеж.

Задача  похожа на предыдущую. Составим уравнение, опираясь на то, что сумма углов треугольника равна \(180{}^\circ \).

\(x+48^{\circ}+90^{\circ}=180^{\circ};\)

\(x=42^{\circ}.\)

Ответ: 42.

Можно решить проще.

Сумма острых углов прямоугольного треугольника равна \(90{}^\circ \).

Тогда \(x+48^{\circ}=90^{\circ};\)

\(x=42^{\circ}.\)

Ответ: 42.

3. Один из острых углов прямоугольного треугольника равен \(34{}^\circ\). Найдите его другой острый угол. Ответ дайте в градусах.

Решение:

Сумма острых углов прямоугольного треугольника равна \(90{}^\circ \). Поэтому второй острый угол равен: \(90{}^\circ -34{}^\circ =56{}^\circ \).

Ответ: 56.

4. Один из углов равнобедренного треугольника равен \(98\) градусов. Найдите один из других его углов. Ответ дайте в градусах.

Решение:

Как вы думаете, может ли равнобедренный треугольник иметь два угла по \(98\) градусов?

Нет, конечно! Ведь сумма углов треугольника равна \(180\) градусов. Значит, один из углов треугольника равен \(98^{\circ}\), а два других равны \(\genfrac{}{}{}{0}{\displaystyle 180-98}{\displaystyle 2}=41^{\circ}\).

Ответ: 41.

5. На рисунке угол 1 равен \(46^{\circ}\), угол 2 равен \(30^{\circ}\), угол 3 равен \(44^{\circ}\). Найдите угол 4. Ответ дайте в градусах.

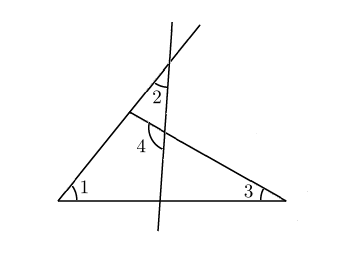
Решение:

Давайте отметим на чертеже еще несколько углов.

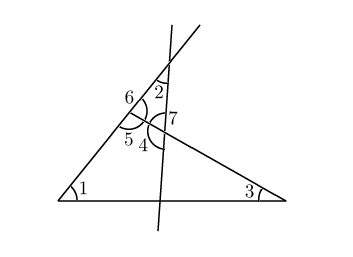
Сначала найдем угол 5.

Он равен \(180^{\circ}-\angle 1-\angle 3 = 90^{\circ}.\)

Тогда \(\angle 6= 90^{\circ};\)

\(\angle 7=180^{\circ}-\angle 2-\angle 6=60^{\circ}.\)

Угол 4, смежный с углом 7 равен \(120^{\circ}.\)

Ответ: 120.

Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.

6. Углы треугольника относятся как \(2:3:4\). Найдите меньший из них. Ответ дайте в градусах.

Решение:

Пусть углы треугольника равны \(2x, \; 3x\) и \(4x\). Запишем, чему равна сумма углов этого треугольника.

\(2x+3x+4x=180^{\circ};\)

\(9x=180^{\circ};\)

\(x=20^{\circ};\)

Тогда \(2x=40^{\circ}.\)

Здесь мы тоже составили уравнение и решили его. Так же, как на уроках алгебры.

Ответ: 40.

7. В треугольнике \(ABC\) известно, что \(AB=BC, \; \angle ABC=108{}^\circ\). Найдите угол \(BCA\). Ответ дайте в градусах.

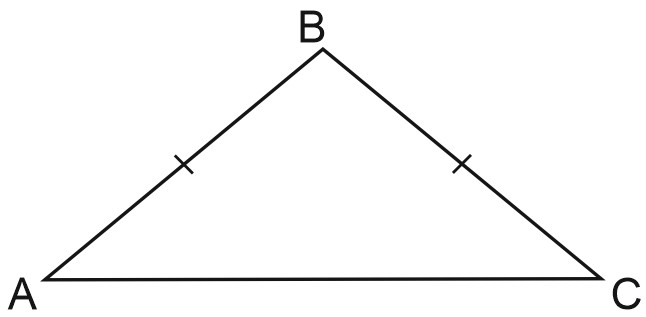
Решение:

В треугольнике \(ABC\) известно, что \(AB=BC\). Значит, треугольник \(ABC\) равнобедренный, и углы при основании \(AC\) равны:

\(\angle A=\angle C=\displaystyle \frac{180{}^\circ -108{}^\circ }{2}=36{}^\circ \).

Ответ: 36.