Материал для повторения:
Четные и нечетные функции.
Что такое параметр. Простые задачи с параметром.
Графический метод решения задач с параметрами.
Встречались ли вам в задаче 18 Профильного ЕГЭ по математике страшные-престрашные уравнения с параметрами? Такие, на которые смотришь – и вообще не понимаешь, что делать?
Есть множество «инструментов» для решения задач с параметрами — методов, приемов, больших и маленьких секретов. Конечно, эти приемы лучше не изобретать на экзамене, а изучить заранее.
Например, использование четности функций, входящих в уравнение.
1. Найдите все значения \(a\), при каждом из которых уравнение
\(x^{2}+c^{2}=\left | x-c \right |+\left | x+c \right |\) имеет единственное решение.
Решение:
Можем ли мы применить графический метод? На первый взгляд кажется, что можем.
Мы помним, как выглядит график функции \(y=\left | x-c \right |+\left | x+c \right |\).
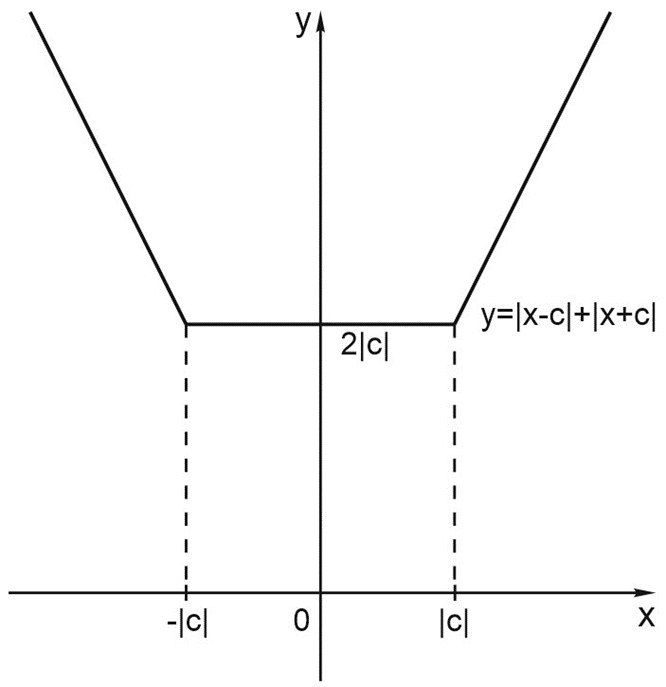
Это график функции в правой части уравнения. А в левой части уравнения - функция \(y=x^{2}+c^{2}\). Ее график также может двигаться в зависимости от параметра \(c\).
Пусть график функции \(y=\left | x-c \right |+\left | x+c \right |\) стоит на месте, а парабола двигается. Вот, кажется, нашли такое расположение, что у графиков двух функций ровно одна общая точка.
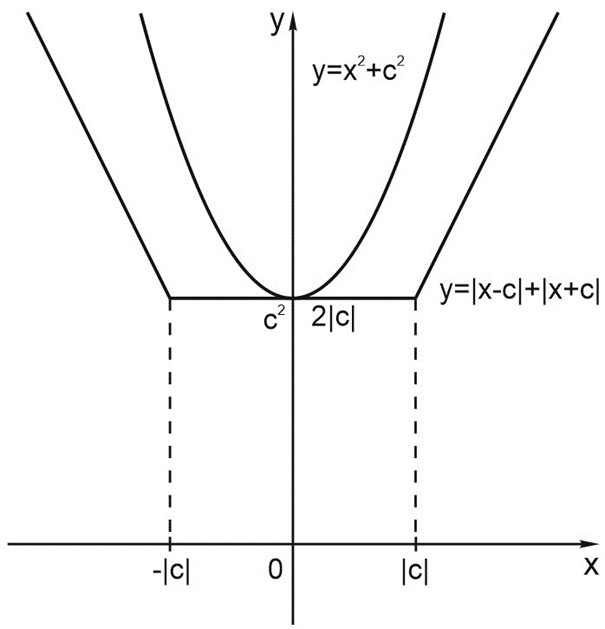
Или все-таки не одна? Может быть, за границами рисунка ветви графиков пересекутся? Как проверить?
Похоже, что наш любимый графический метод здесь не поможет. Нужно что-то другое.
Есть специальный метод – использование четности функций, входящих в уравнение. Он удобен тем, что вы действуете четко по алгоритму и быстро приходите к ответу.
Посмотрим еще раз на уравнение:
\(x^{2}+c^{2}=\left | x-c \right |+\left | x+c \right |.\)
В левой части – четная функция. В правой – тоже.
\(y(-x)=\left | -x-c \right |+\left | -x+c \right |=\left | x+c \right |+\left | x-c \right |=y(x).\)
Получается, что все функции, входящие в уравнение, четны относительно \(x\). Это значит, что если заменить \(x\) на \(–x,\) уравнение не изменится. И если \(x_0\) – корень данного уравнения, то и \(-x_0\) тоже его корень.
Уравнение может иметь единственное решение, только если его корень \(x_0=0\).
Подставим \(x=0\) в уравнение: \(c^{2}=2\left|c\right|\).
Решим это уравнение, сделав замену: \(\left|c\right |=b, \; b\geqslant 0\).
Получим, что \(b=0\) или \(b=2\).
Значит, \(c=0\) или \(c=2\) или \(c=-2\).
Но решение не закончено. Мы примерно на полпути к ответу.
Мы выяснили, что если \(c=0\), \(c=2\) или \(c=-2\), то уравнение имеет корень \(x=0\). Но мы не знаем пока, будет ли этот корень единственным. Возможно, что при каком-то из этих значений параметра уравнение имеет корень \(x=0\) и еще пару корней, равных по модулю и отличающихся знаком. Например, его корни \(0\), \(2\) и \(-2\). Такой случай нам не подходит.
И поэтому нам надо подставить по очереди \(c=0, \; c=2\) и \(c=-2\) в исходное уравнение. Решить его при этих значениях параметра. И выбрать такие значения параметра, при которых исходное уравнение имеет единственный корень.
При \(c=0\) имеем: \(x^{2}=2\left | x \right |\). Такое уравнение мы только что решили, только вместо \(x\) в нем фигурировала переменная \(c\). У него три корня: \(0\), \(2\) и \(-2\), и значит, \(c=0\) не подходит.
Пусть \(c=2\).
Получим: \(x^{2}+4=\left | x-2 \right |+\left | x+2 \right |\).
В этом уравнении два модуля. Применим метод интервалов для модулей. Рассмотрим уравнение по отдельности на трех интервалах, на которые точки \(x=-2\) и \(x=2\) разбивают числовую прямую.
1) На интервале \(x\leqslant-2\) оба модуля раскрываем с противоположным знаком.
\(\left\{\begin{matrix}
x\leqslant -2, \\
x^2+4=-x+2-x-2;\end{matrix}\right.\)
\(\left\{\begin{matrix}
x\leqslant -2,\\
x^2+4=-2x.\end{matrix}\right.\)
Уравнение \(x^2+2x+4=0\) не имеет решений, так как \(D=4-16<0.\)
Значит, на интервале \(x\leqslant-2\) уравнение решений не имеет.
2) Если \(-2< x\leq 2\), первый модуль раскрываем с «минусом», второй – с «плюсом».
\(x^2+4=x-2-x-2;\)
\(\left\{\begin{matrix}
-2< x\leqslant 2, \\
x^2+4=-x+2+x+2.\end{matrix}\right.\)
Уравнение \(x^2=0\) имеет единственный корень \(x=0\) лежащий на промежутке \((-2; 2]\).
3) Если \(x>2\) оба модуля раскрываем с «плюсом»:
\(\left\{\begin{matrix}
x>2, \\
x^2+4=x-2+x+2;\end{matrix}\right.\)
\(\left\{\begin{matrix}
x>2, \\
x^2-2x+4=0.\end{matrix}\right.\)
Снова квадратное уравнение, не имеющее решений.
Значит, на интервале \((2;+\infty)\) уравнение не имеет корней.
При \(c=2\) уравнение имеет единственный корень \(x=0\).
Надо ли отдельно рассматривать случай \(c=-2\)?
Нет, не обязательно. Исходное уравнение четно относительно параметра \(c\), то есть не меняется при замене \(c\) на \(–c.\) Значит, при \(c=-2\) уравнение также имеет единственный корень \(x=0\).
Ответ: \(c=2\) или \(c=-2\).
2. При каких значениях параметра \(a\) система
\(\left\{\begin{matrix}
2^{\ln y}=4^{\left | x \right |},\\
\log _{2}\left ( x^{4}y^{2}+2a^{2} \right )=\log _{2}\left ( 1-ax^{2}y^{2} \right )+1
\end{matrix}\right. \; \) имеет единственное решение?
Найти это значение \(a\). Найти решение.
Решение:
Перед нами система из двух уравнений, в которой есть две переменные \(x\) и \(y\), а также параметр \(a\).
Решать такую систему, выражая, например, \(y\) через \(x\) и подставляя во второе уравнение? — Страшно даже думать об этом!
Для начала запишем ОДЗ — область допустимых значений системы.
ОДЗ: \(\left\{\begin{matrix}
1-ax^{2}y^{2}> 0,\\
y> 0.
\end{matrix}\right.\)
Заметим, что все функции, входящие в уравнения системы, четны относительно \(x\). А вот это уже что-то.
Это значит, что если \(x\) — решения, то \(\left (-x \right )\) – тоже решение. Единственное решение возможно, если \(x=0\).
Подставим \(x=0\) в уравнения системы.
Получим:
\(\left\{\begin{matrix}
2^{\ln y}=1,\\
\log _{2}2a^{2}=1,
\end{matrix}\right.\) отсюда \(2a^{2}=2,\) следовательно \(\left[\begin{array} {ccc}
a=1,\\
a=-1.
\end{array}
\right.\)
1) Если \(a=1,\) то \(\log _{2}\left ( x^{4}y^{2}+2 \right )=\log _{2}\left ( 1-x^{2}y^{2} \right )+1.\)
Получаем: \(\left\{\begin{matrix}
1-x^{2}y^{2}> 0,\\
x^{4}y^{2}+2 = 2-2x^{2}y^{2}.
\end{matrix}\right.\)
\(y^{2}\left ( x^{4} +2x^{2}\right )=0\Rightarrow x=0\) – единственное решение, так как \(y> 0\).
Подставив \(x=0\) в первое уравнение исходной системы, получили, что \(y=1\).
2) Если \(a=-1\), то
\(\log _{2}\left ( x^{4}y^{2}+2 \right )=\log _{2}\left ( 1+x^{2}y^{2} \right )+1;\)
\(x^{4}y^{2}+2 = 2+2x^{2}y^{2}.\)
\(y^{2}\left ( x^{4}-2x^{2} \right )=0\Leftrightarrow \left [
\begin{array} {ccc}
x=0,\\
x=\sqrt{2},\\
x=-\sqrt{2}
\end{array}
\right.\) – 3 решения. Это нам не подходит.
Ответ: \(a=1\). При этом система имеет единственное решение \(\left ( 0;1 \right )\).
3. Найдите все значения параметра \(a\) при каждом из которых система уравнений
\(\left\{\begin{matrix}
a(x^4+4)=y+2(1-|x|),\\
|x|+|y|=2\end{matrix}\right. \; \) имеет единственное решение.
Решение:
Уравнения системы четны относительно \(x\). Если пара чисел \((x_0;y_0)\) – решение, то пара чисел \((-x_0;y_0)\) тоже будет решением.
Значит, система может иметь единственное решение, только если \(x_0 = 0\). Это решение вида \((0; y)\).
Найдем, при каких значениях параметра \(a\) это произойдет.
Для \(x=0\) система принимает вид:
\(\left\{\begin{matrix}
4a=y+2,\\
|y|=2.\end{matrix}\right.\)
Из второго уравнения: \(y=\pm2\) и тогда \(a=1\) или \(a=0\). Подставим по очереди \(a=1\) и \(a=0\) в исходную систему.
1) Если \(a=1\), получим:
\(\left\{\begin{matrix}
x^4+4=y+2(1-|x|),\\
|x|+|y|=2;\end{matrix}\right.\Leftrightarrow
\left\{\begin{matrix}
y=x^4+2|x|+2, \\
|x|+x^4+2|x|+2=2;\end{matrix}\right. \Leftrightarrow
\left\{\begin{matrix}
y=x^4+2|x|+2, \\
x^4+3|x|=0;\end{matrix}\right. \Leftrightarrow
\left\{\begin{matrix}
y=2, \\
x=0.\end{matrix}\right. \)
Итак, при \(a = 1\) система имеет единственное решение.
2) Пусть \(a= 0\).
\(\left\{\begin{matrix}
0=y+2(1-|x|), \\
|x|+|y|=2;\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
y=2|x|-2, \\
|x|+|2|x|-2|=2.\end{matrix}\right.\)
Решим второе уравнение системы. Сделаем замену: \(|x| = t, \; t\geqslant 0\).
\(t+|2t-2|=2.\)
Корни этого уравнения \(t=0\) и \(t=\displaystyle \frac{4}{3}\). Им соответствуют \(3\) значения \(x\), и значит, при \(a=0\) у системы будет более одного решения. Подходит только \(a=1\).
Ответ: \(a=1\).
































