Касательная к окружности

Касательная к окружности – прямая, имеющая с окружностью единственную общую точку.

Расскажем подробнее, что такое касательная и секущая.

Напомним, что расстояние от точки до прямой — это длина перпендикуляра, опущенного из точки на прямую.

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности. В этом случае она имеет с окружностью ровно одну общую точку.

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках. Такую прямую называют секущей.

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не имеет с окружностью общих точек.

Запишем основные теоремы о касательных. Они помогут нам при решении задач ЕГЭ и ОГЭ.

Теорема 1. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

На рисунке радиус \(OA\) перпендикулярен прямой \(m\).

Теорема 2. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Доказательство:

Дана окружность с центром \(O\).

Прямые \(AB\) и \(AC\) — касательные, точки \(B\) и \(C\) — точки касания. Докажем, что \(AB= AC\) и \(\angle BAO=\angle CAO\).

Проведем радиусы \(OB\) и \(OC\) в точки касания.

По свойству касательной, \(OB\bot AB\) и \(OC\bot AC\).

В прямоугольных треугольниках \(AOB\) и \(AOC\) катеты \(OB\) и \(OC\) равны как радиусы одной окружности, \(AO\) — общая гипотенуза. Следовательно, треугольники \(AOB\) и \(AOC\) равны по гипотенузе и катету. Отсюда \(AB = AC\) и \(\angle BAO=\angle CAO\).

Теорема 3. Отрезки касательных, проведенных к окружности из одной точки, равны.

Доказательство:

Пусть из точки \(A\) к окружности проведены касательные \(AB\) и \(AC\). Соединим точку \(A\) с центром окружности точкой \(O\). Треугольники \(AOB\) и \(AOC\) равны по гипотенузе и катету, следовательно, \(AB = AC\).

Теорема 4. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

 

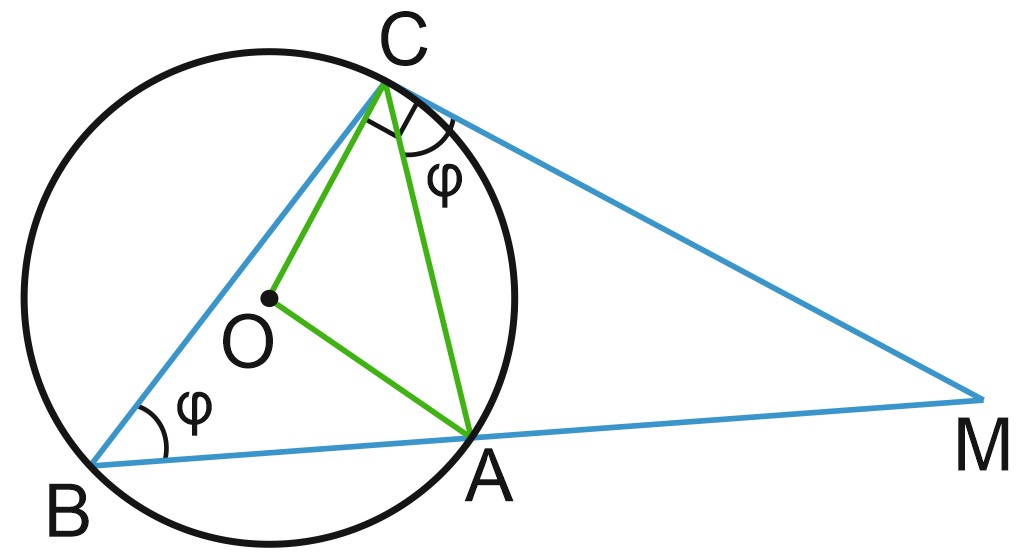
Угол \(ACM\) на рисунке равен половине угловой величины дуги \(AC\).

Доказательство теоремы здесь.

Теорема 5, о секущей и касательной. Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.

\(MC^2 = MA \cdot MB\)

Доказательство теоремы смотрите здесь.

Задачи ЕГЭ и ОГЭ по теме «Касательная к окружности»

1. Угол \(ACO\) равен \(28^{\circ}\), где \(O\) — центр окружности. Его сторона \(CA\) касается окружности. Найдите величину меньшей дуги \(AB\) окружности, заключенной внутри этого угла. Ответ дайте в градусах.

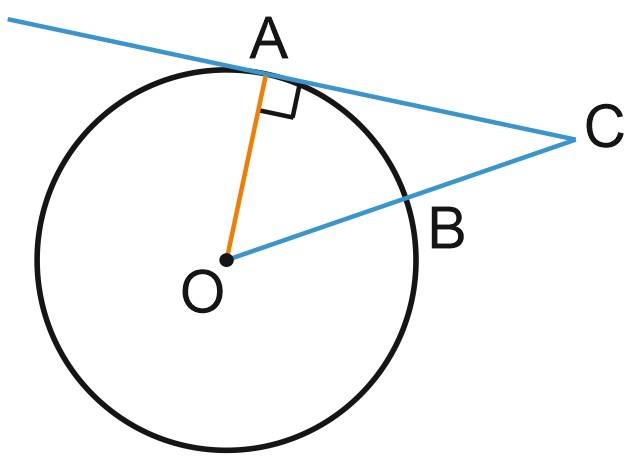
Решение:

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол \(CAO\) — прямой.

Из треугольника \(ACO\) получим, что угол \(AOC\) равен \(62\) градуса.

Bеличина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги \(AB\) — тоже \(62\) градуса.

Ответ: 62.

2. Найдите угол \(ACO\), если его сторона \(CA\) касается окружности, \(O\) — центр окружности, а большая дуга \(AD\) окружности, заключенная внутри этого угла, равна \(116^{\circ}\). Ответ дайте в градусах.

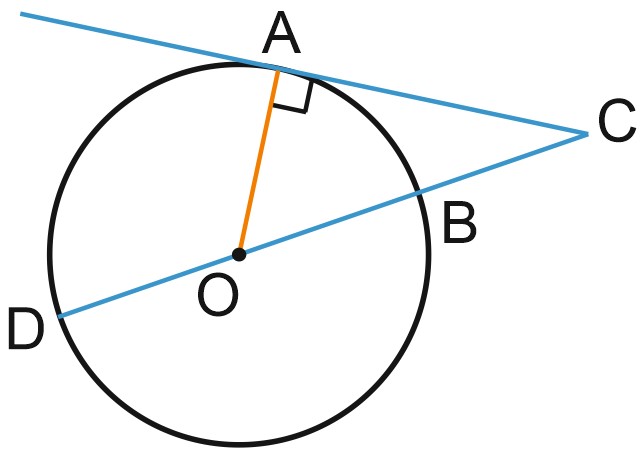
Решение:

Это чуть более сложная задача.

Центральный угол \(AOD\) опирается на дугу \(AD\), следовательно, он равен \(116\) градусов. Тогда угол \(AOC\) равен \(180^{\circ}-116^{\circ}=64^{\circ}\).

Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол \(OAC\) — прямой. Тогда угол \(ACO\) равен \(90^{\circ}-64^{\circ}=26^{\circ}\).

Ответ: 26.

3. Хорда \(AB\) стягивает дугу окружности в \(92^{\circ}\). Найдите угол \(ABC\) между этой хордой и касательной к окружности, проведенной через точку \(B\). Ответ дайте в градусах.

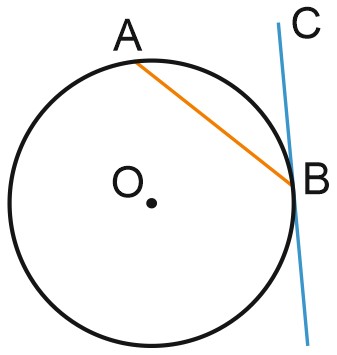
Решение:

Проведем радиус \(OB\) в точку касания, а также радиус \(OA\). Угол \(OBC\) равен \(90^{\circ}\).

Треугольник \(BOA\) — равнобедренный. Нетрудно найти, что угол \(OBA\) равен \(44\) градуса, и тогда угол \(CBA\) равен \(46\) градусов, то есть половине угловой величины дуги \(AB\).

Мы могли также воспользоваться теоремой: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

4. К окружности, вписанной в треугольник \(ABC\), проведены три касательные. Периметры отсеченных треугольников равны \(6, \; 8, \; 10\). Найдите периметр данного треугольника.

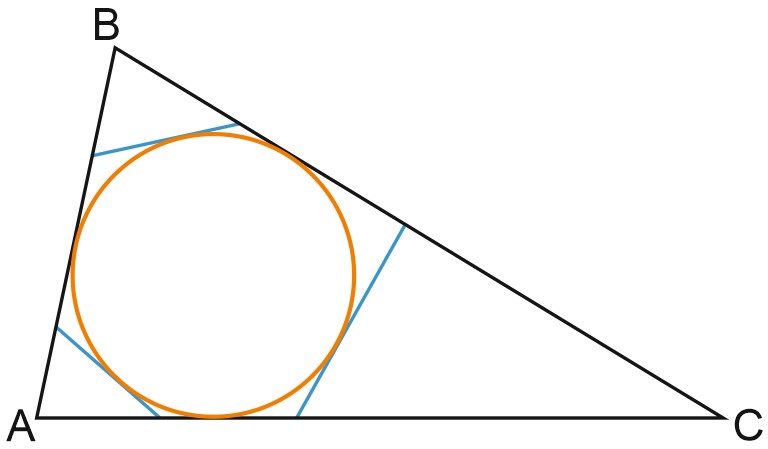
Решение:

Вспомним еще одно важное свойство касательных к окружности:

Отрезки касательных, проведенных из одной точки, равны.

Периметр треугольника — это сумма всех его сторон.

Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом.

Постарайтесь увидеть, как периметр треугольника \(ABC\) складывается из периметров отсеченных треугольников.

Ответ: 24.

Вот более сложная задача из вариантов ЕГЭ:

5. Около окружности описан многоугольник, площадь которого равна \(5\). Его периметр равен \(10\). Найдите радиус этой окружности.

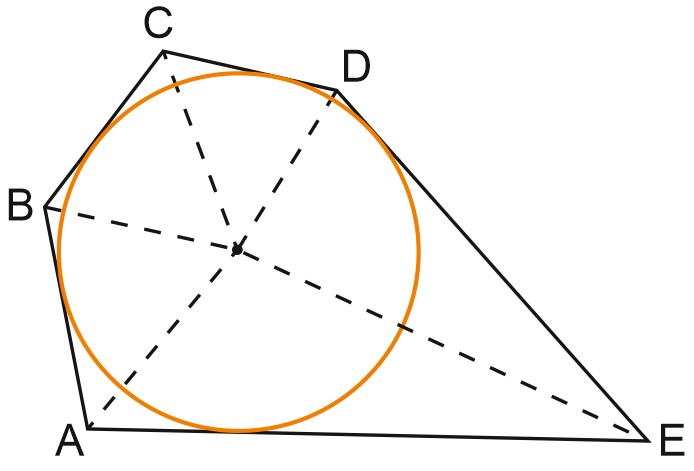
Решение:

Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.

Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку \(O\) — и проведите перпендикулярные сторонам радиусы в точки касания.

Соедините точку \(O\) с вершинами \(A, \; B, \; C, \; D, \; E\). Получились треугольники \(AOB, \; BOC, \; COD, \; DOE, \; EOA\).

Очевидно, что площадь многоугольника \(S=S_{AOB} + S_{BOC}+S_{COD}+S_{DOE}+S_{EOA}\).

Треугольники \(AOB, \; BOC, \; COD, \; DOE, \; EOA\) имеют равные высоты, причем все эти высоты равны радиусу окружности.

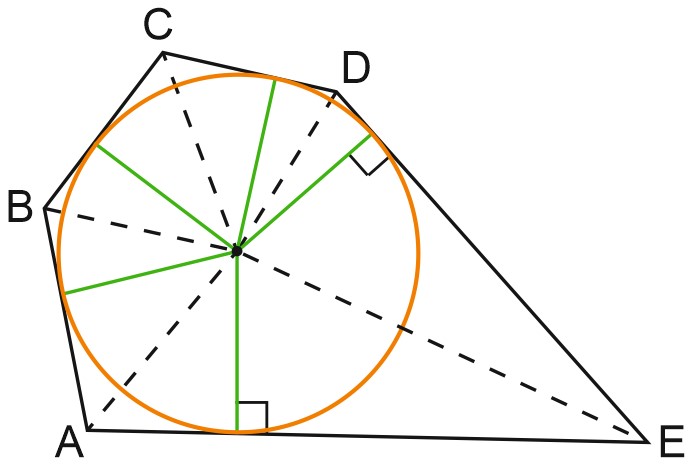
\(S_{ABCDE}=S_{\vartriangle AOB}+S_{\vartriangle BOC}+S_{\vartriangle COD}+S_{\vartriangle DOE}+S_{\vartriangle EOA}=\)

\(=\displaystyle \frac{1}{2}AB\cdot r+\displaystyle \frac{1}{2}BC\cdot r+\displaystyle \frac{1}{2}CD\cdot r+\displaystyle \frac{1}{2}DE\cdot r+\displaystyle \frac{1}{2}AE\cdot r=\)

\(=\displaystyle \frac{1}{2}\cdot r\cdot \left(AB+BC+CD+DE+EA\right)=\displaystyle \frac{1}{2}P\cdot r=p\cdot r\), где \(p\) — полупериметр многоугольника.

По условию, \(P= 10, \; S = 5\), тогда \(r=\displaystyle \frac{S}{p}=\displaystyle \frac{5}{5}=1\).

Ответ: 1

6. Угол \(ACO\) равен \({27}^\circ\), где \(O\) — центр окружности. Его сторона \(CA\) касается окружности. Сторона \(CO\) пересекает окружность в точке \(B\). Найдите величину меньшей дуги \(AB\) окружности. Ответ дайте в градусах.

Решение:

По условию, \(CA\) — касательная, \(AO\) — точка касания.

\(OA\bot AC\). Треугольник \(ACO\) — прямоугольный, \(\angle AOC=90{}^\circ -\angle ACO=90{}^\circ -27{}^\circ =63{}^\circ \).

Угол \(\angle AOB\) — центральный, и он равен угловой величине дуги \(AB\), на которую опирается. Значит, градусная мера дуги \(AB\) равна \(63{}^\circ \).

Это меньшая дуга \(AB\), а большая — с другой стороны от точек \(A\) и \(B\), и она больше \(180\) градусов.

Ответ: 63.

7. Через концы \(A\) и \(B\) дуги окружности с центром \(O\) проведены касательные \(AC\) и \(BC\). Меньшая дуга \(AB\) равна \({58}^\circ\). Найдите угол \(ACB\). Ответ дайте в градусах.

Решение:

Центральный угол \(AOB\) равен угловой величине дуги, на которую он опирается, то есть \(58{}^\circ \).

\(AC\) и \(BC\) — касательные, поэтому \(\angle OAC=\angle OBC=90{}^\circ \), поскольку касательная перпендикулярна радиусу, проведенному в точку касания.

Сумма углов четырехугольника \(ACBO\) равна \(360{}^\circ \).

\(\angle ACB=360{}^\circ -90{}^\circ -90{}^\circ -58{}^\circ =122{}^\circ \).

Ответ: 122.

8. Хорда \(AB\) стягивает дугу окружности в \({92}^\circ\). Найдите угол \(ABC\) между этой хордой и касательной к окружности, проведенной через точку \(B\). Ответ дайте в градусах.

Решение:

Применим теорему об угле между касательной и хордой.

Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.

Значит, угол \(ABC\) равен \(46{}^\circ \).

Ответ: 46.

9. Через концы \(A\) и \(B\) дуги окружности с центром \(O\) проведены касательные \(AC\) и \(BC\). Угол \(CAB\) равен \(32{}^\circ\). Найдите угол \(AOB\). Ответ дайте в градусах.

Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.

Поэтому меньшая дуга \(AB\) окружности равна \(64{}^\circ\). Центральный угол равен угловой величине дуги, на которую он опирается, значит, угол \(AOB\) равен \(64{}^\circ\).

Мы могли бы решить задачу и по-другому, рассматривая четырехугольник \(ACBO\), как в задаче 2.

Ответ: 64.

10. Через концы \(A\) и \(B\) дуги окружности в \({62}^\circ\) проведены касательные \(AC\) и \(BC\). Найдите угол \(ACB\). Ответ дайте в градусах.

Решение:

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.

В треугольнике \(ABC\):

\(\angle ACB=180{}^\circ -\left(\angle BAC+\angle CBA\right)=180{}^\circ -\cup AB=180{}^\circ -62{}^\circ =118{}^\circ \).

Ответ: 118.

11. Найдите угол \(ACO\), если его сторона \(CA\) касается окружности, \(O\) — центр окружности, сторона \(CO\) пересекает окружность в точках \(B\) и \(D\), а дуга \(AD\) окружности, заключенная внутри этого угла, равна \(116{}^\circ\). Ответ дайте в градусах.

Решение:

По условию, \(DB\) — диаметр окружности, поэтому дуга \(AB\), не содержащая точки \(D\), равна \(180{}^\circ - 116{}^\circ = 64{}^\circ\).

На эту дугу опирается центральный угол \(AOB\), он равен \(64{}^\circ\).

Треугольник \(AOC\) прямоугольный, так как касательная \(CA\) перпендикулярна радиусу \(OA\), проведенному в точку касания.

\(\angle ACO=90{}^\circ -\angle COA=90{}^\circ -64{}^\circ =26{}^\circ \).

Ответ: 26.

12. К окружности с центром в точке \(O\) проведены касательная \(AB\) и секущая \(AO\). Найдите радиус окружности, если \(AB = 12\) см, \(AO= 13\) см.

Решение:

Отрезок \(OB\) — радиус, проведённый в точку касания, поэтому \(AB\) и \(OB\) перпендикулярны, треугольник \(AOB\) — прямоугольный. По теореме Пифагора:

\({OB}^2={AO}^2-{AB}^2\);

\({{OB}^2=13}^2-{12}^2=169-144=25;\; OB=5\).

Ответ: 5.

13. Прямая касается окружности в точке \(K\). Точка \(O\) — центр окружности. Хорда \(KM\) образует с касательной угол, равный \({83}^\circ\). Найдите величину угла \(OKM\). Ответ дайте в градусах.

Решение:

Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому угол \(OKD\) — прямой.

Тогда \(\ \angle OKM\ =\ 90{}^\circ - 83{}^\circ = 7{}^\circ \).

Треугольник \(OMK\) — равнобедренный, его стороны \(OK\) и \(OM\) являются радиусами окружности, поэтому \(\angle OMK\ =\angle \ OKM= 7{}^\circ \).

Ответ: 7.

14. Отрезок \(AB= 40\) касается окружности радиуса \(75\) с центром \(O\) в точке \(B\). Окружность пересекает отрезок \(AO\) в точке \(D\). Найдите \(AD\).

Решение:

Касательная перпендикулярна радиусу, проведенному в точку касания, значит, треугольник \(AOB\) — прямоугольный. Из прямоугольного треугольника \(AOB\) по теореме Пифагора найдём \(AO\):

\(AO=\sqrt{{AB}^2+{OB}^2}=\sqrt{{40}^2+{75}^2}=\sqrt{5^2\left(8^2+{15}^2\right)}=5\cdot 17=85\);

\(AD=AO\ -\ OD=85-\ 75=10.\)

Ответ: 10.

15. На отрезке \(AB\) выбрана точка \(C\) так, что \(AC= 75\) и \(BC= 10\). Построена окружность с центром \(A\), проходящая через \(C\). Найдите длину отрезка касательной, проведённой из точки \(B\) к этой окружности.

Решение:

Проведём радиус \(AH\) в точку касания. Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому треугольник \(ABH\) — прямоугольный.

Из прямоугольного треугольника \(ABH\) по теореме Пифагора найдём \(BH\):

\(BH=\sqrt{{AB}^2-{AH}^2}=\sqrt{{\left(AC+CB\right)}^2-{AH}^2}=\sqrt{{85}^2-{75}^2}=\sqrt{5^2\left({17}^2-{15}^2\right)}=40\).

Ответ: 40.

16. Касательные в точках \(A\) и \(B\) к окружности с центром \(O\) пересекаются под углом \({72}^\circ\). Найдите угол \(ABO\). Ответ дайте в градусах.

Решение:

Касательные, проведённые к окружности из одной точки, равны, поэтому \(AC=BC\) и треугольник \(ABC\) — равнобедренный.

\(\angle CAB=\angle CBA=\displaystyle \frac{180{}^\circ -\angle ACB}{2}=54{}^\circ \).

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними, значит, дуга \(AB\) равна \({108}^\circ\). Угол \(AOB\) — центральный, он равен дуге, на которую опирается, то есть \({108}^\circ\).

Треугольник \(AOB\) равнобедренный, \(\angle OAB=\angle ABO=\displaystyle \frac{180{}^\circ -108{}^\circ }{2}=36{}^\circ \).

Ответ: 36.

17. Из точки \(A\) проведены две касательные к окружности с центром в точке \(O\). Найдите радиус окружности, если угол между касательными равен \({60}^\circ\), а расстояние от точки \(A\) до точки \(P\) равно \(8\).

Решение:

Проведём радиусы \(OB\) и \(OC\) в точки касания. Треугольники \(AOB\) и \(AOC\) — прямоугольные. Эти треугольники равны по катету и гипотенузе.

\(OB=OC\) как радиусы окружности, гипотенуза общая. Значит, \(\angle BAO=\angle OAC=\displaystyle \frac{60{}^\circ }{2}=30{}^\circ \).

Из треугольника \(AOB\) найдём \(OB\), то есть радиус окружности.

\(OB=AO\cdot {\sin 30{}^\circ \ }=8\cdot \displaystyle \frac{1}{2}=4\).

Ответ: 4.

18. Через точку \(A\), лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке \(K\). Другая прямая пересекает окружность в точках \(B\) и \(C\), причём \(AB = 2, \; AC = 8\). Найдите \(AK\).

Решение:

По теореме о секущей и касательной, \({AK}^2=AB\cdot AC\);

\(AK=\sqrt{AB\cdot AC}=\sqrt{2\cdot 8}=4\).

Ответ: 4.

19. На окружности отмечены точки \(A\) и \(B\) так, что меньшая дуга \(AB\) равна \({72}^\circ\). Прямая \(BC\) касается окружности в точке \(B\) так, что угол \(ABC\) острый. Найдите угол \(ABC\). Ответ дайте в градусах.

Решение:

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.

\(\angle ABC = 72{}^\circ : 2 = 36{}^\circ \).

Ответ: 36.