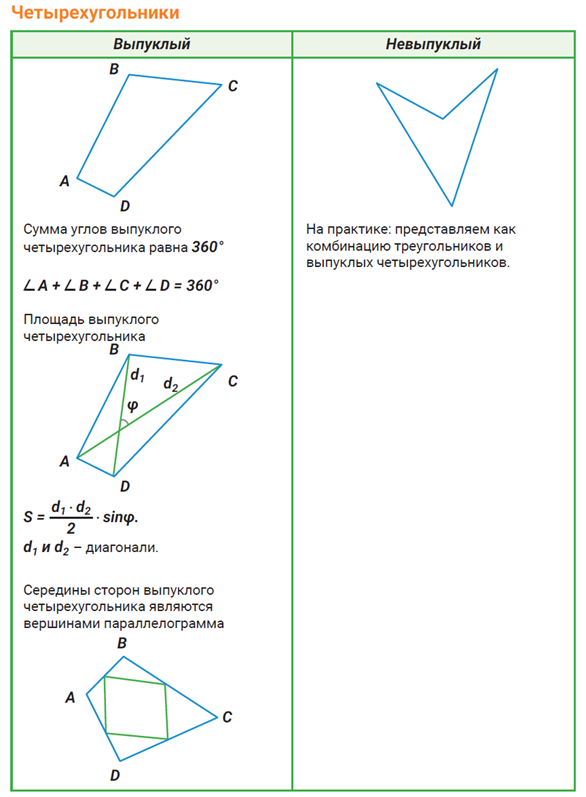
Четырехугольники. Сумма углов четырехугольника

В школьных задачах по геометрии мы обычно рассматриваем выпуклые четырехугольники.

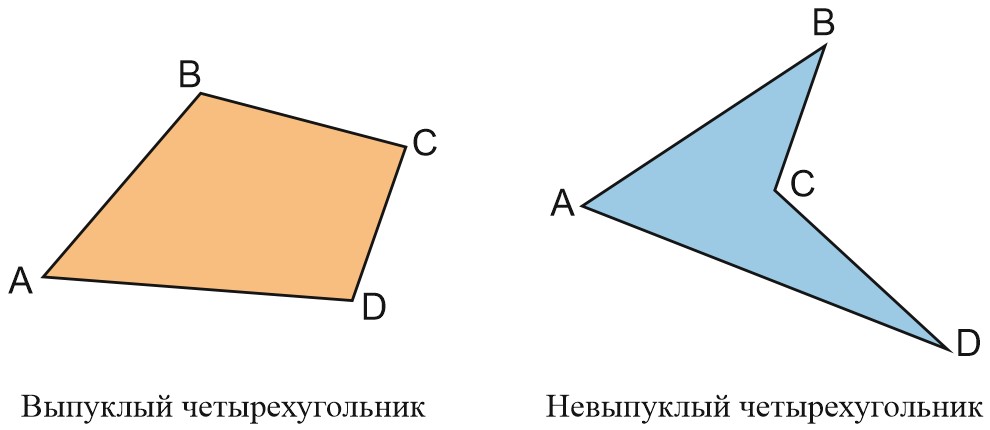
В чем разница между ними? Если любые две точки выпуклого многоугольника соединить отрезком – весь отрезок будет лежать внутри многоугольника. Для невыпуклых фигур это не выполняется.

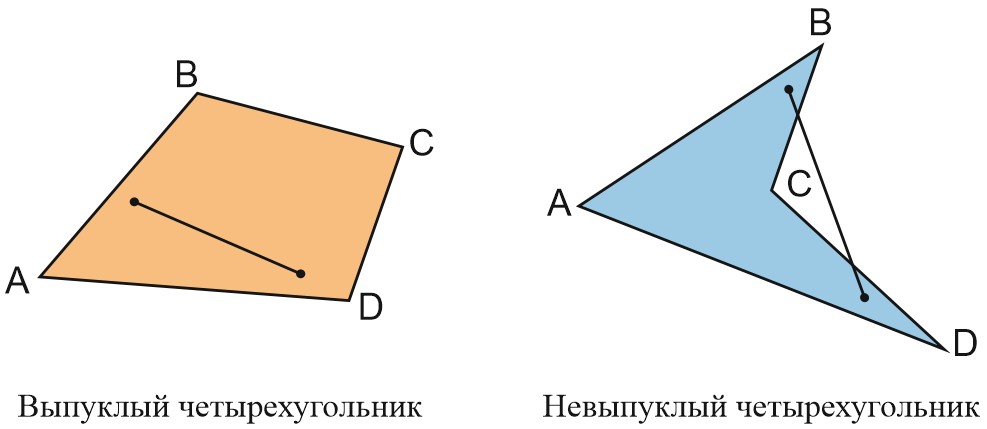
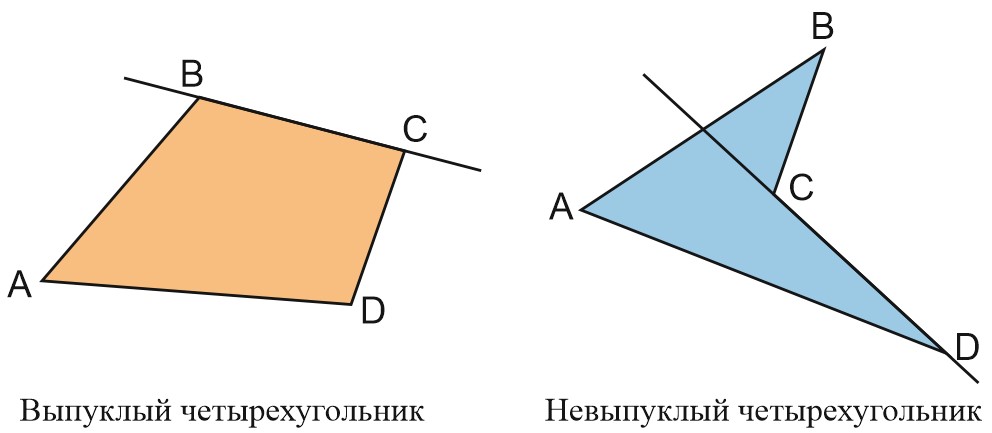
Можно сказать и по-другому. Если через любую из сторон выпуклого многоугольника провести прямую, то весь выпуклый многоугольник будет лежать с одной стороны от этой прямой. Для невыпуклого это не выполняется.

Сумма углов выпуклого четырехугольника равна \(360\) градусов.

Этот полезный факт мы часто применяем в задачах. Давайте докажем его.

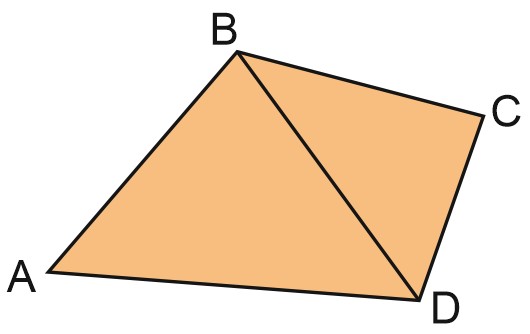
Соединим вершины \(B\) и \(D\) четырехугольника \(ABCD.\)

Мы получили два треугольника, \(ABD\) и \(BCD.\)

Найдем сумму углов четырехугольника. Она равна:

\(\angle BAD+\angle ABC+\angle BCD+\angle CDA=\angle BAD+\angle ABD+\angle ADB+\angle CBD+\angle BCD+\angle CDB=\)

\(=180^{\circ}+180^{\circ}=360^{\circ}.\)

Мы воспользовались тем, что сумма углов треугольника равна \(180\) градусов.

А если нам встречается в задаче невыпуклый четырехугольник, мы обычно разбиваем его на треугольники.

Для выпуклого четырехугольника справедлива теорема Вариньона.

Середины сторон выпуклого четырехугольника являются вершинами параллелограмма.

Докажем эту теорему.

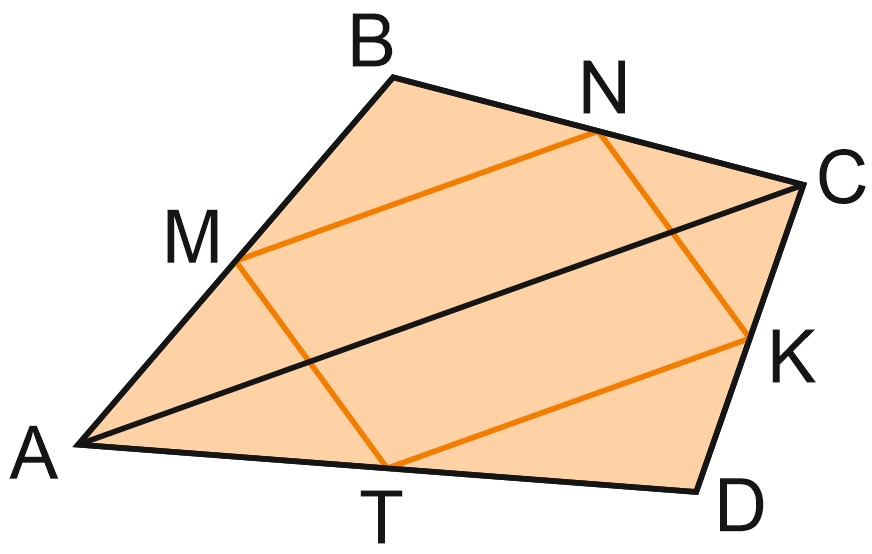
Пусть точки \(M, \; N, \; K, \; T\) – середины сторон \(AB, \; BC, \; CD, \; DA\) четырехугольника \(ABCD.\)

В треугольнике \(ABC\) отрезок \(MN\) – средняя линия,  \(MN\parallel AC, \; \displaystyle MN=\frac{1}{2}AC.\)

В треугольнике \(ADC\) отрезок \(KT\) – средняя линия,  \(KT\parallel AC, \; \displaystyle KT=\frac{1}{2}AC.\)

Значит, четырехугольник \(MNKT\) – параллелограмм по признаку параллельности. Его противоположные стороны параллельны и равны. Теорема доказана.

Чаще всего в задачах ОГЭ и ЕГЭ встречаются четырехугольники, у которых есть параллельные стороны. Это параллелограмм, ромб, квадрат, прямоугольник и трапеция.

1. В четырехугольнике \(ABCD\) угол \(A\) равен \(43^{\circ},\) угол \(C\) равен \(88^{\circ},\) угол \(D\) равен \(102^{\circ}.\) Найдите угол \(B.\)

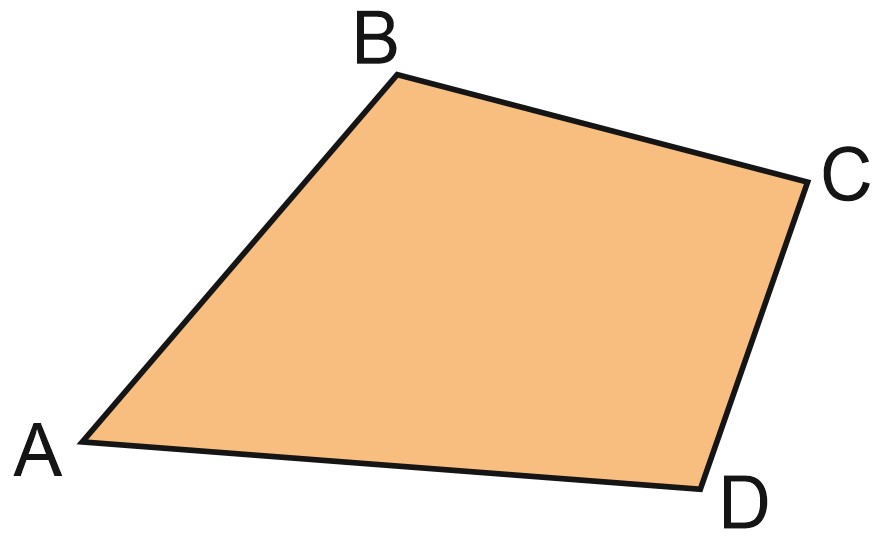
Решение:

Сумма углов четырехугольника \(ABCD\) равна \(360^{\circ}.\)

Тогда угол B равен \(360^{\circ} - 43^{\circ} - 88^{\circ} - 102^{\circ}=127^{\circ}.\)

Ответ: 127.

2. В выпуклом четырёхугольнике \(ABCD\) известно, что \(AB=BC, \; AD=CD, \; \angle B=61{}^\circ , \; \angle D=151{}^\circ .\) Найдите величину угла \(A\). Ответ дайте в градусах.

Решение:

Если соединить точки \(B\) и \(D\), получим два равных треугольника. Они равны по трем сторонам. В равных треугольниках напротив равных сторон лежат равные углы.

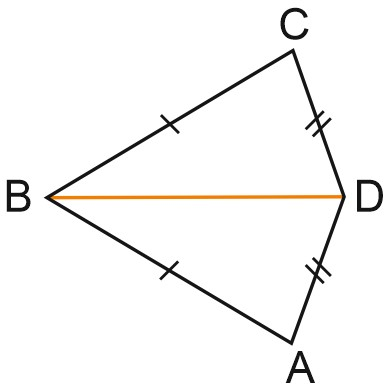
В треугольнике \(ABD\) сумма двух углов

\(\angle DBA+\angle BDA=\displaystyle \frac{1}{2}\left(\angle B+\angle D\right)=\displaystyle \frac{1}{2}\left(61+151\right)=106{}^\circ .\)

Тогда \(\angle A=180{}^\circ -106=74{}^\circ \), по теореме о сумме углов треугольника.

Ответ: 74.

Читаем дальше: Как найти площадь выпуклого четырехугольника.

Соберем свойства четырехугольников в одну таблицу: