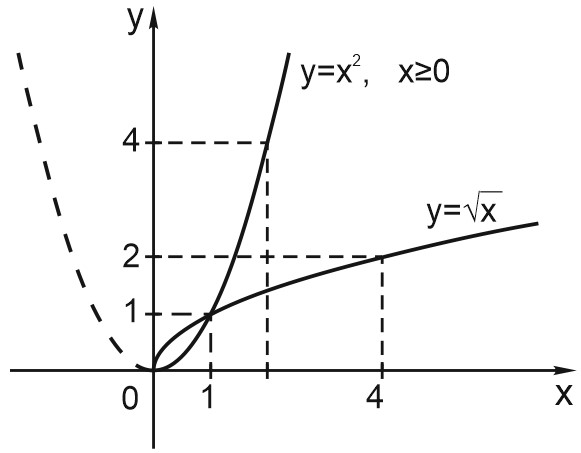Степенная функция

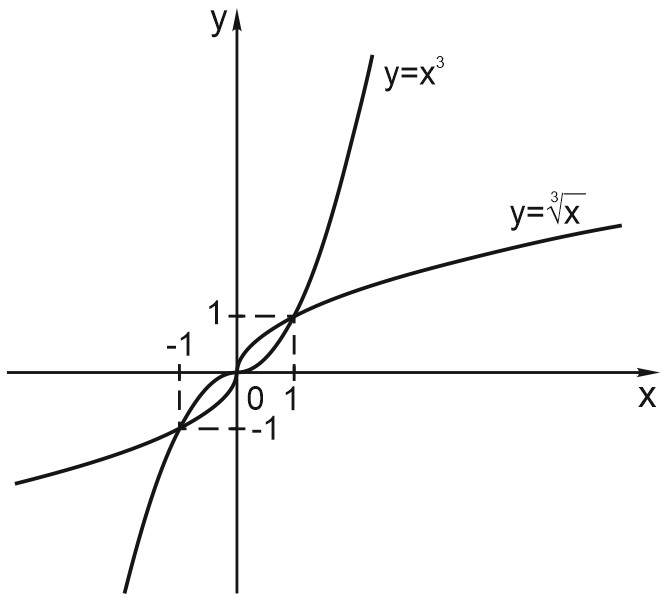
Степенны́ми называют функции вида \(x^{a}\), где \(a\) может быть целым, дробным, положительным или отрицательным. К ним относятся всем знакомая линейная функция \(y = kx + b\), парабола \(y = x^{2}\) (в общем виде: \(y = ax^{2} + bx + c)\), кубическая парабола \(y = x^{3}\). Степенными являются также гипербола \(y = \displaystyle \frac{1}{x}\), которую можно представить как \(y = x^{-1}\), функция \(y =\sqrt{x }\) (ведь \(\sqrt{x} = x^{\frac{1}{2}}\)), \(y=\sqrt[3]{x}\)  и многие другие.

Расскажем подробно об этих функциях и их графиках.

1. Линейная функция \(y = kx + b\). График — прямая линия. Для её построения достаточно двух точек.

Если \(k > 0\), линейная функция возрастает. Чем больше \(k\), тем круче идет график. Число \(k\) называется угловым коэффициентом прямой и равно тангенсу угла наклона этой прямой к положительному направлению оси \(X\):

Если \(k < 0\), линейная функция убывает. Очевидно, в этом случае угол \(\alpha\)   — тупой и \(tg\alpha  < 0\).

Если \(k = 0\), мы получим прямую \(y = b\), параллельную оси \(X\).
Если угловые коэффициенты прямых равны — прямые параллельны.

2. О квадратичной функции (параболе) \(y=ax^{2}+bx+c\) мы уже рассказывали.

Кратко повторим основные моменты:

- Если \(a > 0\), ветви параболы направлены вверх. Если \(a < 0\) — вниз.

- Координаты вершины параболы находятся по формулам: \(x_{0}=\displaystyle -\frac{b}{2a}, \; y_{0}=y(x_{0}).\)

- Точки пересечения параболы с осью \(X\) находятся как корни квадратного уравнения \(y=ax^{2}+bx+c=0\). Если корней нет (дискриминант уравнения меньше нуля), парабола не пересекает ось \(X\).

- Точку пересечения параболы с осью \(Y\) находим, подставив в её уравнение \(x=0\).

3. На рисунках функции \(y = x^{3}\) (кубическая парабола), \(y = x^{4}\) и \(y = x^{5}.\)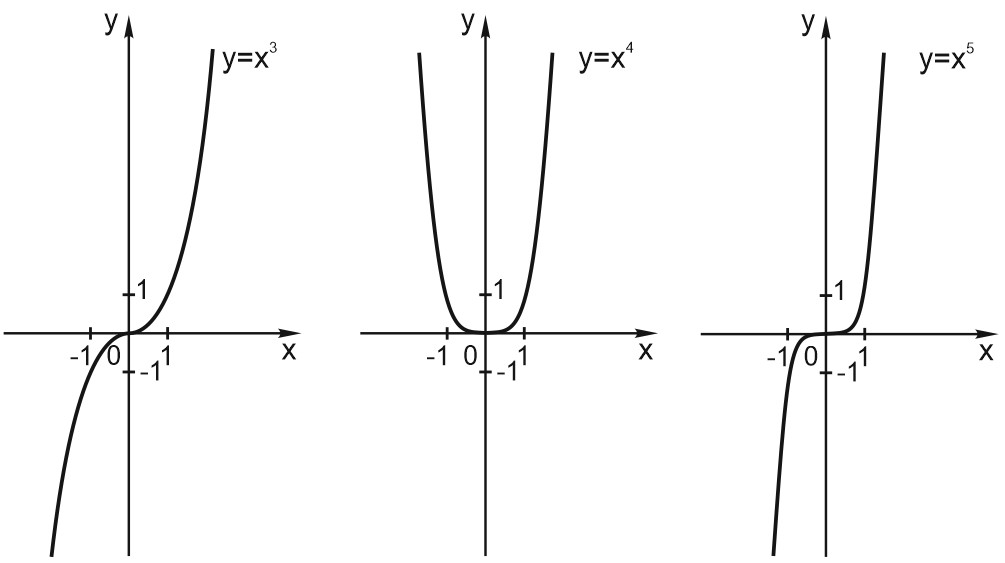

4. Заметим, что между функциями \(y = x^{2}\) и \(y = x^{4}.\) есть определенное сходство. Оба этих графика симметричны относительно оси \(Y\). Такие функции называются чётными.

Определение. Функция \(y = f(x)\) называется чётной, если:

1) область определения функции симметрична относительно нуля;

2) для каждого \(x\) из области определения выполняется равенство \(f(−x) = f(x)\).

Графики функций \(y = x^{3}\) и \(y = x^{5}\) симметричны относительно начала координат. Эти функции — нечётные.

Определение. Функция \(y = f(x)\) называется нечётной, если:

1) область определения функции симметрична относительно нуля;

2) для каждого \(x\) из области определения выполняется равенство \(f(-x) = -f(x)\).

Очевидно, функция \(y=x^{a}\) является чётной при чётных значениях \(a\) и нечётной при нечётных \(a\).

5. Функция \(y = \displaystyle \frac{1}{x}\) (гипербола) также относится к степенным. Ведь \(\displaystyle \frac{1}{x} = x^{-1}\). Поскольку знаменатель не должен обращаться в ноль, эта функция не определена при \(x=0\). Гипербола является нечётной функцией. Её график симметричен относительно начала координат.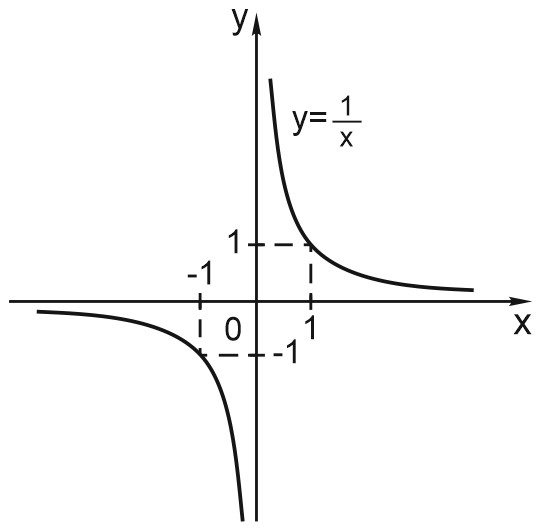

6. Построим график функции \(y= \sqrt{x}\).

Выражение \(\sqrt{x}\) определено при \(x\geq  0\), поэтому область определения функции — все неотрицательные числа.

Кроме того, \(y = \sqrt{x}\) принимает только неотрицательные значения, поскольку \(\sqrt{x}\geq 0.\)

Мы используем эти свойства при решении уравнений и неравенств. Уравнение вида \(\sqrt{f(x)}=g(x)\) имеет смысл только при \(f(x)\geq 0\) и \(g(x)\geq 0\). Это его область допустимых значений.

Существуют вопросы, ставящие в тупик почти любого абитуриента. Например, чему равен \(\sqrt{a^{2}}\)?

Правильный ответ: \(\sqrt{a^{2}}=\left| a\right|\).

Запомните это. Проверить легко: возьмём, например, \(a = −2\).

\((-2)^{2} = 4;\)

\(\sqrt{4 }= 2.\)

Изобразим на одном графике параболу \(y = x^{2}\) и функцию \(y = \sqrt{x}\).

Сейчас нас интересует правая ветвь параболы, при \(x\geq  0\). Мы видим, что эта часть параболы и график функции \(y = \sqrt{x}\) словно нарисованы по одному шаблону, по-разному расположенному в координатной плоскости. Они симметричны относительно прямой \(y = x\). То, что для одной из них — область определения, для другой — область значений.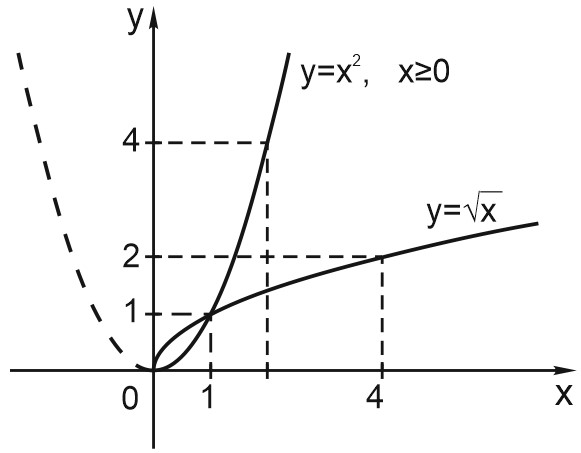

Напомним, что такие функции называются взаимно обратными. Подробно об этом можно прочитать в статье «Логарифмическая функция».

7. Легко убедиться, что функция \(y = \sqrt[3]{x}\) является обратной к функции \(y = x^{3}\).