Трапеция и ее свойства

Т. А. Унегова

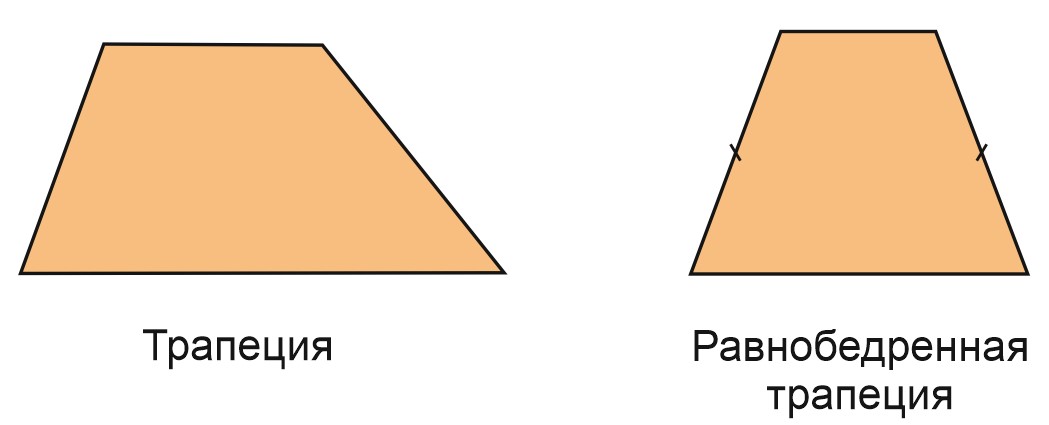
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные – боковыми сторонами трапеции.

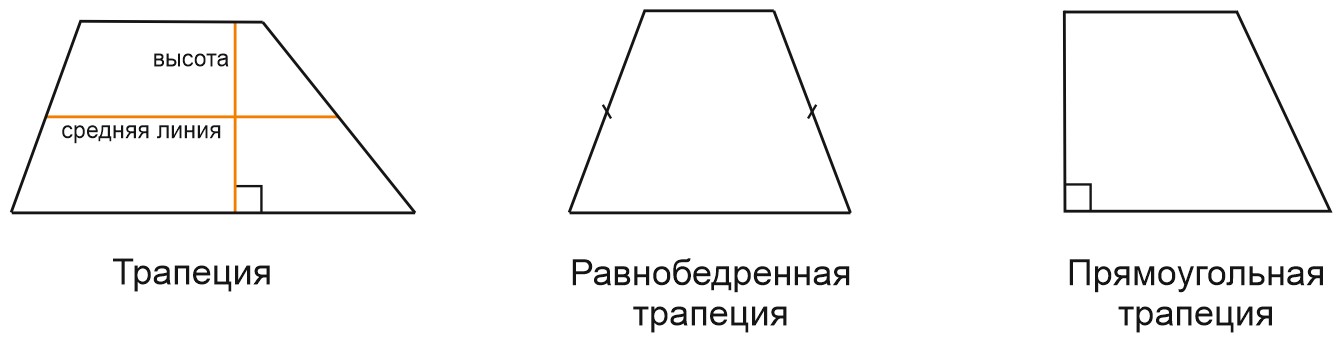
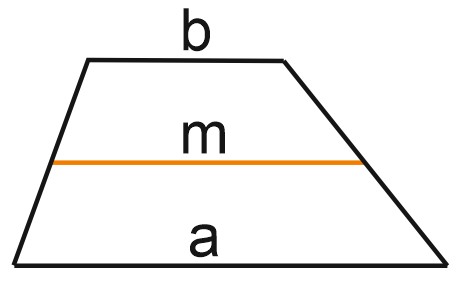
Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция равнобедренная.

Высота трапеции – перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Свойства трапеции:

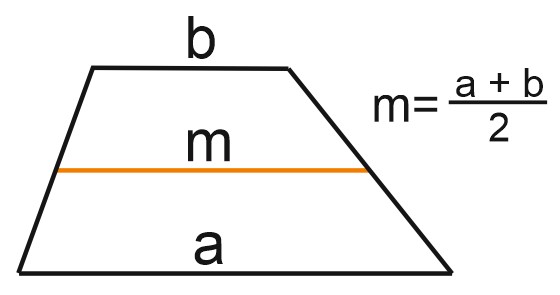
1) Средняя линия трапеции параллельна основаниям и равна их полусумме: \(m=\displaystyle \frac{a+b}{2}.\)

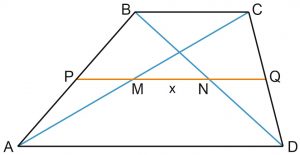
2) Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

Доказательство здесь.

3) Проекция боковой стороны равнобедренной трапеции на основание равна полуразности основания, а проекция диагонали – полусумме оснований.

Доказательство:

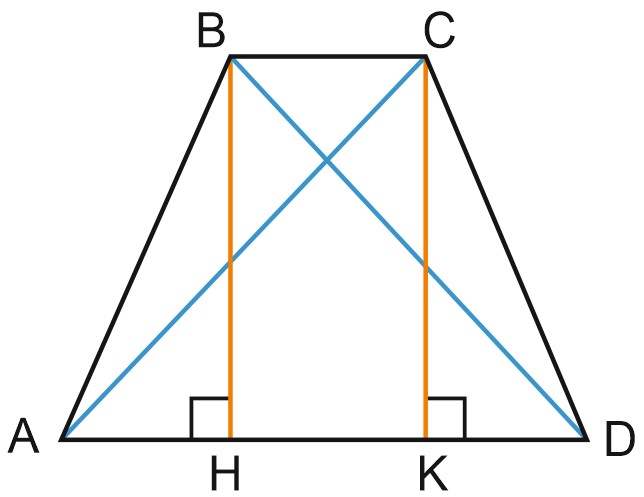
Трапеция \(ABCD\) на рисунке – равнобедренная, \(AB=CD, \; BH\) и \(CK\) – перпендикуляры к \(AD.\)

Тогда \(AH\) и \(KD\) – проекция боковых сторон на основание \(AD, \; AH=KD= \displaystyle \frac{AD-BC}{2}.\)

\(AK\) – проекция диагонали \(AC\) на основание \(AD, \; AK=AH+HK=AH+BC=\displaystyle \frac{AD+BC}{2}.\)

4) Замечательное свойство трапеции. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон – лежат на одной прямой.

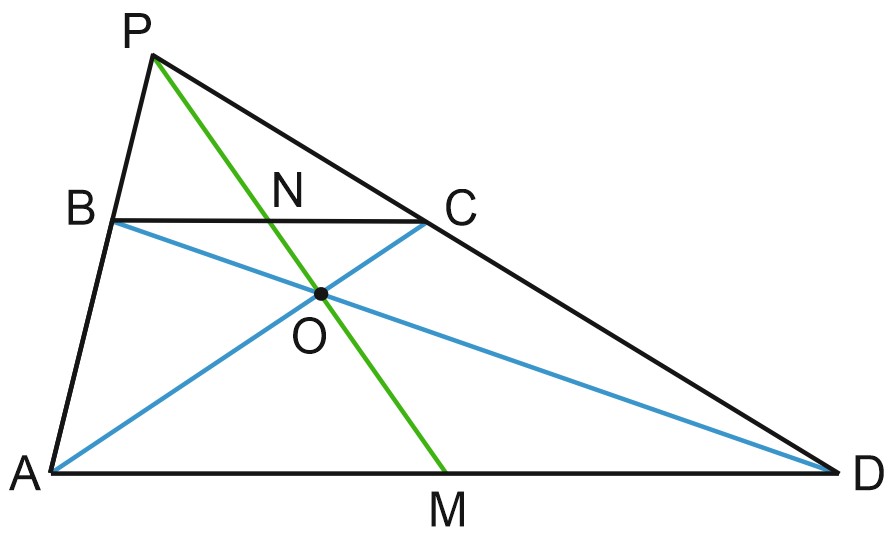
Доказательство здесь.

5) Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, имеют равные площади, а два других, содержащие основания, подобны.

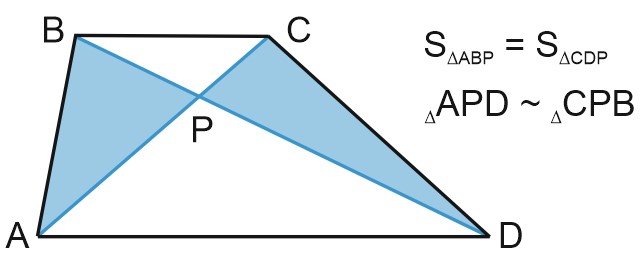
Доказательство:

Площади треугольников \(ABD\) и \(ACD\) равны. У них одно и то же основание \(AD\) и равные высоты, \(S_{\triangle ABD}=S_{\triangle ACD}.\)

Площадь треугольника \(ABD\) равна сумме площадей треугольников \(APD\) и \(ABP\), а площадь треугольника \(ACD\) равна сумме площадей треугольников \(APD\) и \(CPD\).

\(S_{\triangle ABD}=S_{\triangle APD}+S_{\triangle ABP},\)

\(S_{\triangle ACD}=S_{\triangle APD}+S_{\triangle PCD}.\)

Значит, \(S_{\triangle ABP}=S_{\triangle PCD}.\)

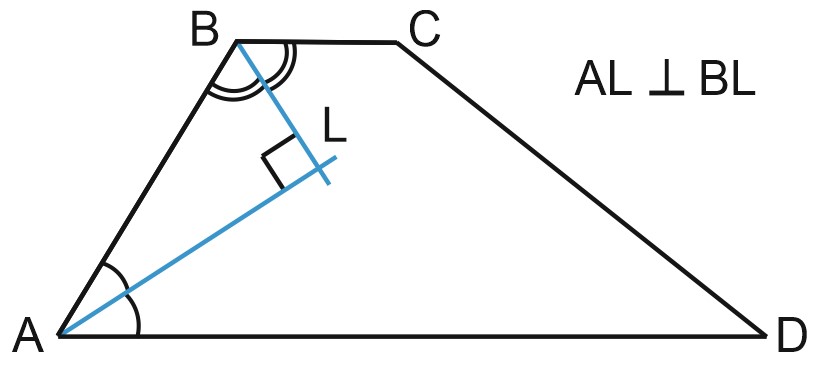
6) Сумма углов трапеции, прилежащих к боковой стороне трапеции, равна \(180\) градусов.

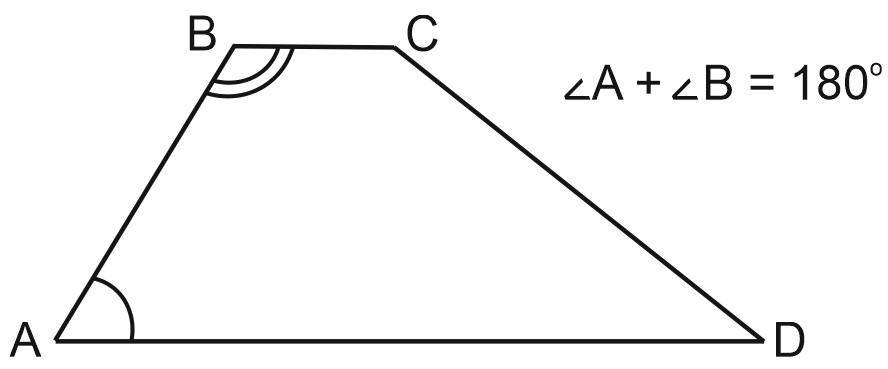
7) Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны (как у параллелограмма).

Задачи ЕГЭ и  ОГЭ по теме «Трапеция»

1. Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.

Решение:

Средняя линия трапеции параллельна основаниям и равна их полусумме: \(m=\displaystyle \frac{a+b}{2}.\)

Значит, \( a+5=2\cdot 11=22, \; a=17. \)

Ответ: 17.

2. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

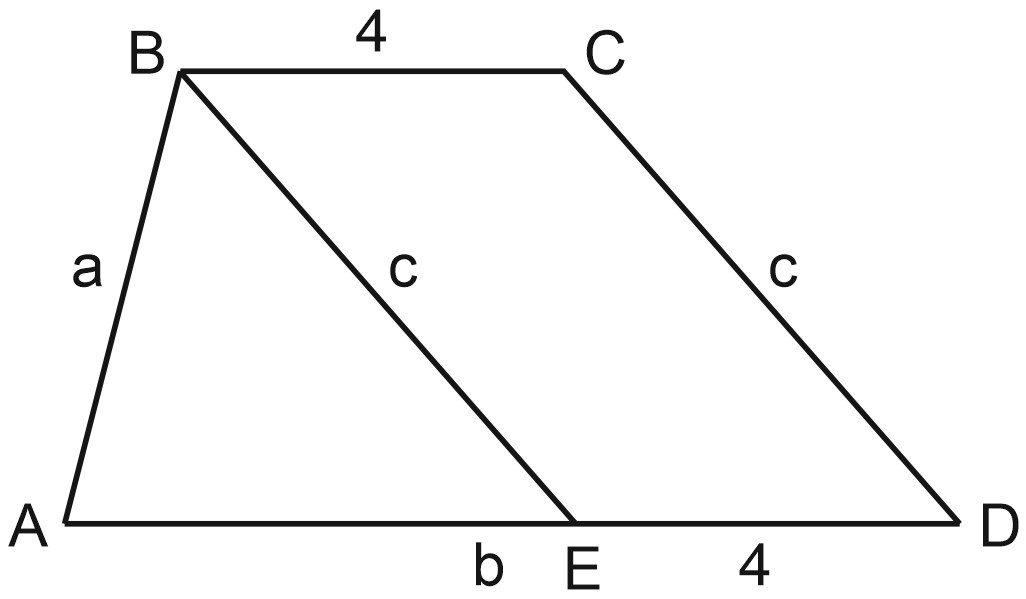
Заметим, что \(BCDE\) – параллелограмм, как как его противоположные стороны попарно параллельны. Значит, \(BE=CD, \; BC=ED.\)

Периметр треугольника равен сумме его сторон, \(a+b+c=15.\)

Периметр трапеции равен \(a+b+4+c+4=(a+b+c)+8=15+8=23.\)

Ответ: 23.

3. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

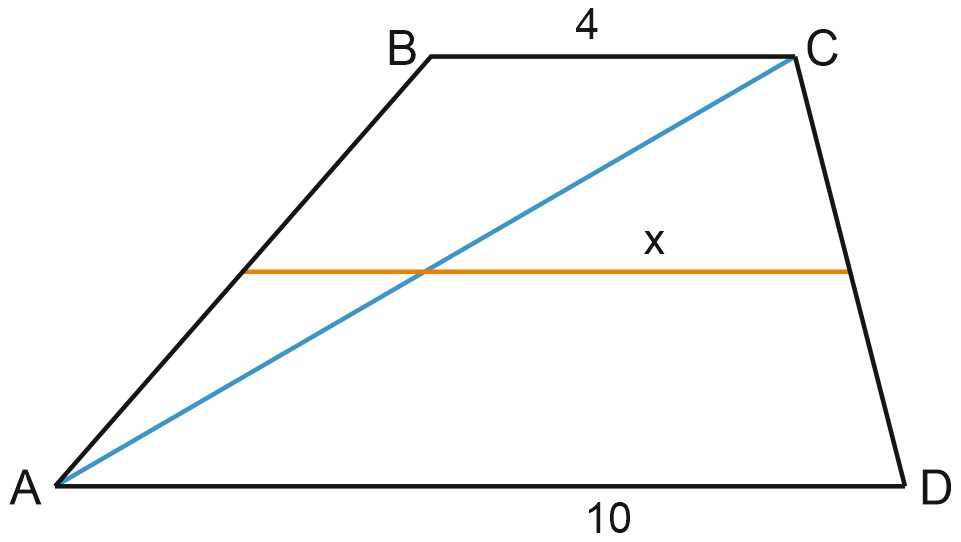
Что мы видим на чертеже? Можно сказать, что изображена трапеция \(ABCD\), и в ней проведена средняя линия. А можно увидеть и другое – два треугольника, \(ABC\) и \(ACD\), в которых проведены средние линии.

Напомним, что средняя линия треугольника – это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны.

Из \(\triangle ACD\) находим, что \(x=5.\)

Ответ: 5.

4. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

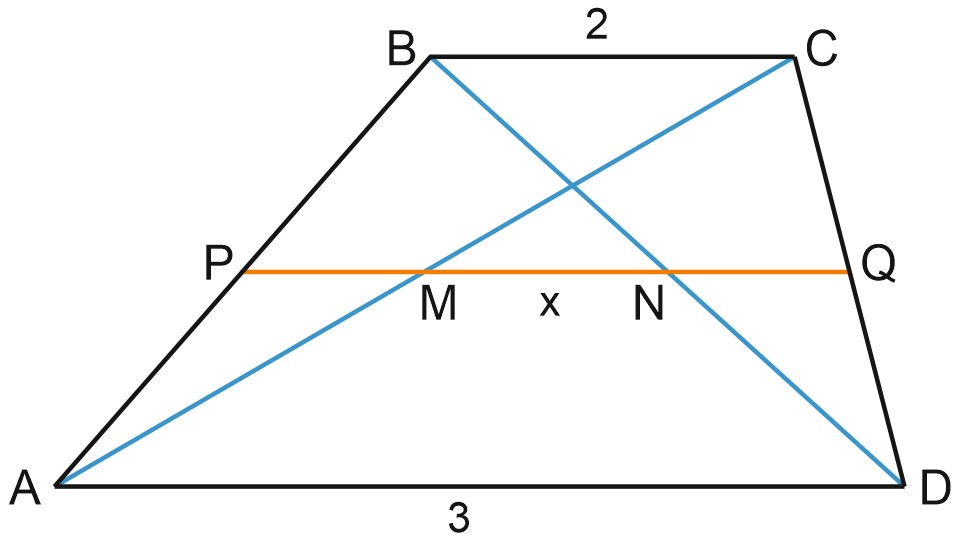
Проведем \(PQ\) – среднюю линию трапеции, \(PQ = 2,5\) и \(PQ\parallel BC\). Отсюда получаем, что \(M\) – середина отрезка \(AC\), то есть \(PM\) – средняя линия треугольника \(ABC\) и \(PM = 1.\) Аналогично, \(NQ = 1.\)

\(x=MN=PQ-PM-NQ=0,5.\)

Ответ: 0,5.

5. Основания трапеции равны 3 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ (отрезок \(MQ\) на рисунке).

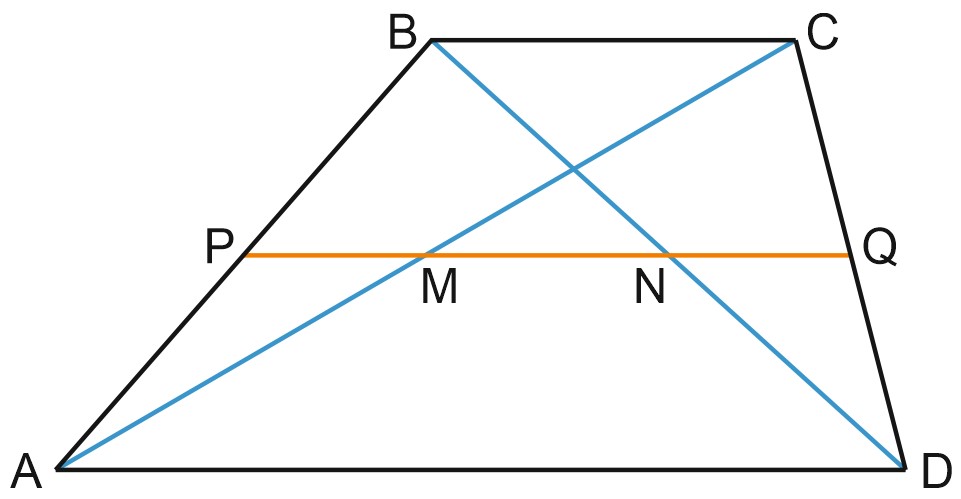
Решение:

Рассмотрим треугольник \(ACD\), в котором проведена средняя линия \(MQ\).

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны.

Из \(\triangle ACD\) находим, что \(MQ=AD:2=9:2=4,5.\)

Ответ: 4,5.

6. В равнобедренной трапеции \(ABCD\) диагональ \(AC\) является биссектрисой острого угла трапеции и образует со стороной \(CD\) угол \(63{}^\circ \). Найдите углы трапеции.

Решение:

Пусть \(\angle CAD =\alpha \), тогда \(\angle CAB=\alpha \) и \(\angle BAD=2\alpha \), так как трапеция равнобедренная.

Сумма углов \(\vartriangle ACD=3\alpha +63{}^\circ =180{}^\circ \), откуда \(\alpha =39{}^\circ .\)

\(\angle D=78{}^\circ \), а \(\angle BCD=180{}^\circ -78{}^\circ =102{}^\circ \), это больший угол.

Ответ: \(102{}^\circ \).

7. Диагонали трапеции \(ABCD\) пересекаются в точке \(M\). Известно, что площадь трапеции равна 38, площадь треугольника \(BCM\) равна 5, а площадь треугольника \(ADM\) в 3 раза больше. Найдите площадь треугольника \(ABM\).

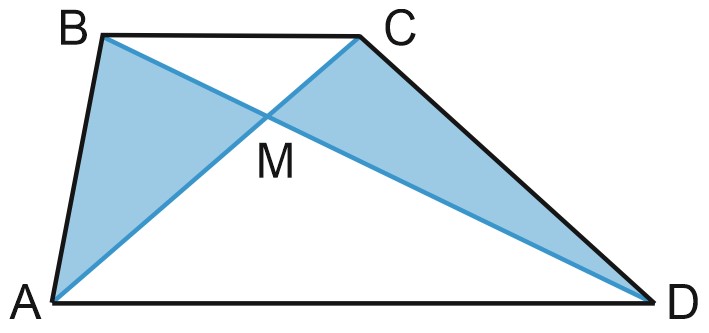
Решение:

Как мы доказали, треугольники \(ABM\) и \(CDM\) имеют равные площади.

Пусть \(S\) – площадь треугольника \(ABM\). Тогда площадь треугольника \(CDM\) тоже равна \(S.\)

Если площадь треугольника \(BCM\) равна 5, то площадь треугольника \(ADM\) равна \(5\cdot 3=15.\)

Площадь трапеции равна сумме площадей четырех треугольников, \(ABM, \; BCM, \; CDM\) и \(ADM.\)

\(S+5+S+15=38,\) отсюда \(S=9.\)

Ответ: 9.

8. Найдите высоту трапеции \(ABCD\), опущенную из вершины \(B\), если стороны квадратных клеток равны \(\sqrt{2}\).

Решение:

Высота трапеции – это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины \(B\). Так как сторона квадратной клетки равна \(\sqrt{2}\) , то по теореме Пифагора получаем, что \(h=2\).

Ответ: 2.

9. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол \({150}^{{}^\circ }\). Найдите площадь трапеции.

Решение:

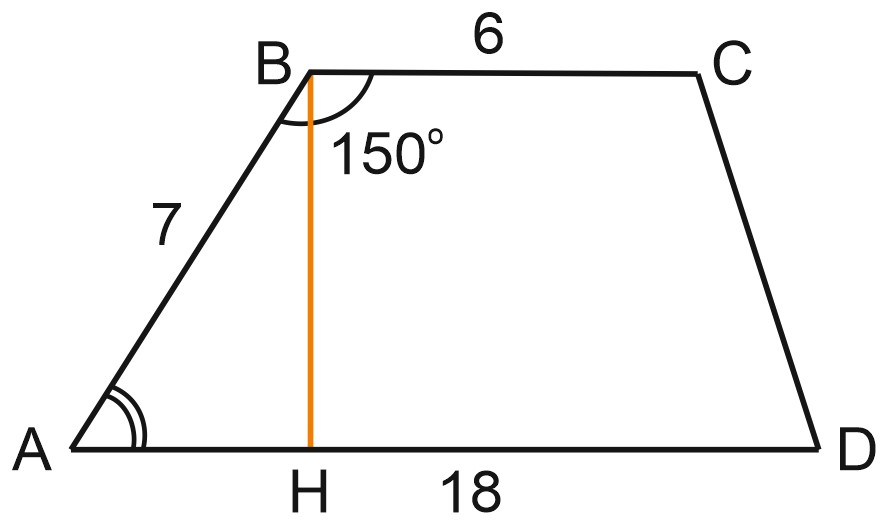
Углы \(\angle ABC\) и \(\angle BAH\) – односторонние, их сумма равна \({180}^{{}^\circ }\), и тогда \(\angle BAH =30{}^\circ .\)

Из \(\vartriangle ABH\) найдем высоту \(BH\). Катет, лежащий против угла в \({30}^{{}^\circ }\), равен половине гипотенузы. Получаем, что \(BH = 3,5.\)

Площадь трапеции равна \(S=\displaystyle \frac{6+18}{2}\cdot 3,5=42.\)

Ответ: 42.

10. В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и \(h^2={25}^2-7^2=\left(25-7\right)\left(25+7\right)=18\cdot 32.\)

Отсюда, \(h=\sqrt{18\cdot 32}=\sqrt{9\cdot 64}=3\cdot 8=24.\)

Ответ: 24.

11. Тупой угол равнобедренной трапеции равен \({135}^\circ \), а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом \(45{}^\circ .\)

Каждый треугольник равнобедренный, поэтому \(h = 1,4.\)

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее – 4,8.

Отсюда площадь трапеции равна \(\displaystyle \frac{2+4,8}{2}\cdot 1,4=4,76.\)

Ответ: 4,76.

12. Площадь трапеции равна 60 м\(^2,\) а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции \(S=\displaystyle \frac{a+b}{2}\cdot h\), то \(60=\displaystyle \frac{8+12}{2}\cdot h\), откуда \(h = 6.\)

Ответ: 6.

13. В равнобедренной трапеции диагонали перпендикулярны и равны \(a\). Найдите площадь трапеции.

Решение:

Проведем \(CE \parallel  BD\) и \(DE\) – продолжение \(AD.\)

Так как \(BCDE\) – параллелограмм, то \(CE = a.\)

По теореме 10 получим, что \(S_{ABCD}=S_{ACE}=\displaystyle \frac{1}{2}a^2.\)

Ответ: \(\displaystyle \frac{1}{2}a^2.\)

14. В трапеции \(ABCD\) с большим основанием \(AD\) диагональ \(AC\) перпендикулярна к боковой стороне \(CD\) и является биссектрисой угла \(A\). Найдите \(AD\), если периметр трапеции равен 20, а угол \(D\) равен \(60{}^\circ \).

Решение:

По условию задачи в прямоугольном \(\vartriangle ACD:\)

\(\angle D=60{}^\circ \), следовательно, \(\angle CAD =30{}^\circ .\)

Так как \(AC\) – биссектриса, то \(\angle CAB =30{}^\circ \), откуда \(\angle DAB =60{}^\circ \), то есть, трапеция равнобедренная. \(\angle BCA =\angle CAD =30{}^\circ \) как накрест лежащие, поэтому \(\vartriangle ABC\) – равнобедренный.

Обозначим длины боковых сторон \(\vartriangle ABC\) буквой \(x\).

Тогда \(AB = BC = CD = x,\) и \(AD = 2x,\) так как в прямоугольном \(\vartriangle ACD\) против угла в \(30{}^\circ \) лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет \(5x\), отсюда

\(x = 4\) и \(AD = 8.\)

Ответ: 8.

15. В равнобедренной трапеции \(ABCD\) с острым углом \(60{}^\circ \) меньшее основание \(BC\) равно 2, а боковая сторона \(AB\) равна 10. Продолжения боковых сторон трапеции пересекаются в точке \(M\). Во сколько раз площадь трапеции больше площади треугольника \(BCM\)?

Решение:

Нетрудно видеть, что \(\vartriangle BCM\) равносторонний и \(BM = 2\), тогда \(AM = 12\) и \(\vartriangle BCM\) подобен \(\vartriangle ADM\) c коэффициентом \(k=12:2=6.\)

Пусть \(S_{BCM}=S_1, \; S_{ADM}=S_2\), тогда

\(S_2=k^2\cdot S_1=36{\cdot S}_1. \)

Площадь трапеции будет равна \(S_{ABCD}=S_2-S_1=36S_1-S_1=35S_1=35S_{BCM}.\)

Ответ: 35.

16. Сумма углов при одном из оснований трапеции равна \(90{}^\circ \). Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке \(E\) и отметим точки \(F\) и \(G\) – середины оснований трапеции.

Так как сумма углов при основании трапеции равна \(90{}^\circ \), то \(\angle BEC=90{}^\circ \), поэтому \(EF\) и \(EG\) – медианы в прямоугольных треугольниках \(BEC\) и \(AED\) соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит \(FG=EG-EF=AG-BF=5-3=2.\)

Ответ: 2.

17. Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна \(S=mh\), а высота трапеции равна диаметру вписанной окружности, то есть \(h=2r, \) то \(24=10\cdot 2r\), откуда \(r=1,2.\)

Ответ: 1,2.

18. Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус \(r\) вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

\(AB+CD=32:2=16,\) откуда \(AB=16-10=6.\)

Сторона \(AB\) равна диаметру окружности, поэтому \(r=3.\)

Ответ: 3.

19. Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

\(m=\displaystyle \frac{a+b}{2}=\displaystyle \frac{c+d}{2}=\displaystyle \frac{40}{2}=20.\)

Ответ: 20.

20. В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как \(AD\) – диаметр окружности, то дуга \(ABCD\) равна \(180{}^\circ \). Она делится на три равные части по \(60{}^\circ .\)

Вписанный угол \(D\) опирается на дугу \(ABC\), которая равна \(120{}^\circ \), отсюда \(\angle ADC=60{}^\circ \) и, стало быть, \(\angle C=120{}^\circ =\angle B.\)

Ответ: 120.