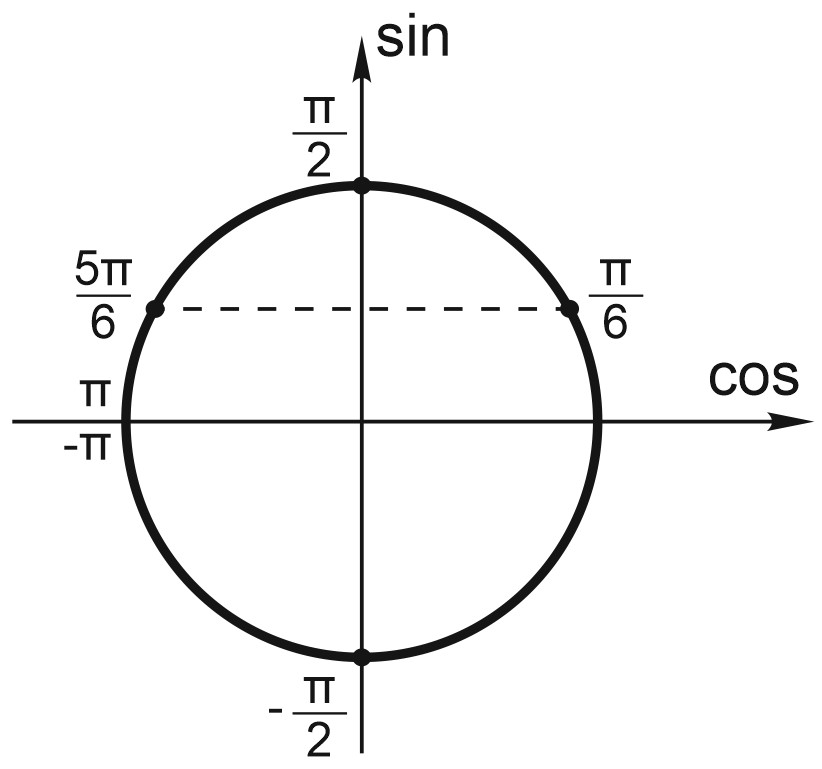
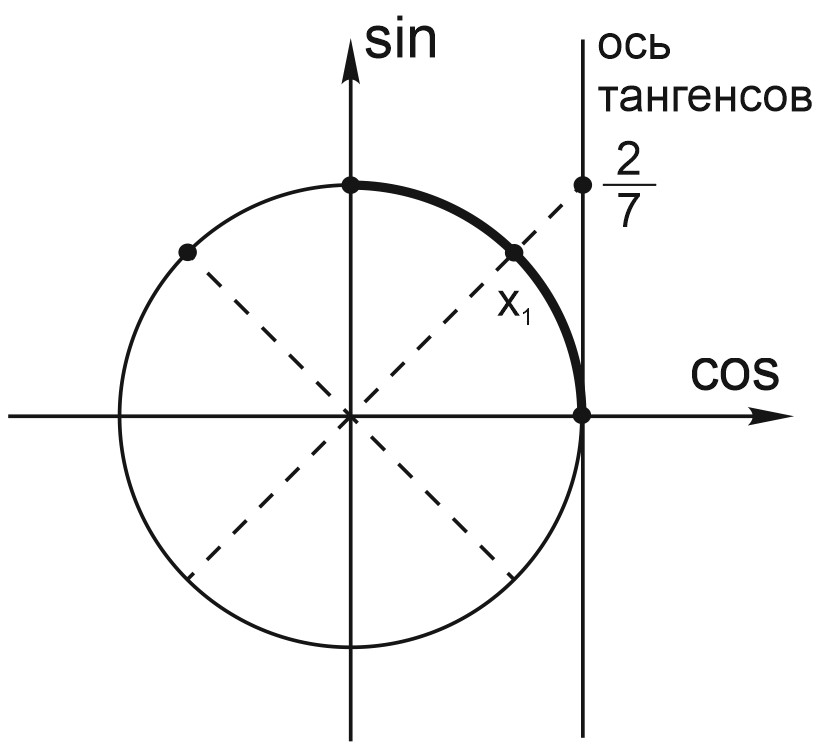
б) Найдем корни уравнения, принадлежащие отрезку \(\displaystyle \left [ 0; \frac{\pi }{2} \right ],\) с помощью единичной окружности. Для этого отметим на ней данный отрезок и найденные серии решений.
Видим, что данному отрезку принадлежит только точка \(\displaystyle x_1=arctg\frac{2}{7}.\)
Ответ: а) \(\displaystyle -\frac{\pi }{4}+\pi k; \; arctg\frac{2}{7}+\pi k, \; k\in Z.\)
к оглавлению ▴
Введение дополнительного угла
Этот метод применяется для уравнений вида \(acosx + bsinx=c\). Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа \(a\) и \(b\) являются значениями синуса и косинуса углов в \(30^{\circ }, \; 45^{\circ }\) или \(60^{\circ }.\)
9. а) Решим уравнение: \(\sqrt{3}sinx+cosx=2.\)
б) Найдите все корни уравнения на отрезке \([0; 3\pi ].\)
Решение:
Делим обе части на \(2\):
\(\displaystyle \frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx=1.\)
Замечаем, что \(\displaystyle \frac{\sqrt{3}}{2}=cos\frac{\pi }{6}; \; \frac{1}{2}=sin\frac{\pi }{6}:\)
\(\displaystyle cos\frac{\pi }{6}sinx+sin\frac{\pi }{6}cosx=1.\)
В левой части получили синус суммы:
\(\displaystyle sin\left ( x+\frac{\pi }{6} \right )=1,\) отсюда \(\displaystyle x+\frac{\pi }{6}=\frac{\pi }{2}+2\pi n, \; n\in Z; \; x=\frac{\pi }{3}+2\pi n, \; n\in Z.\)
б) Отметим на единичной окружности отрезок \([0; 3\pi ].\) и найденные серии решений.
Обратите внимание, что в этой задаче отрезок больше, чем полный круг. Как нам поступить? Один из способов – нарисовать рядом две окружности.
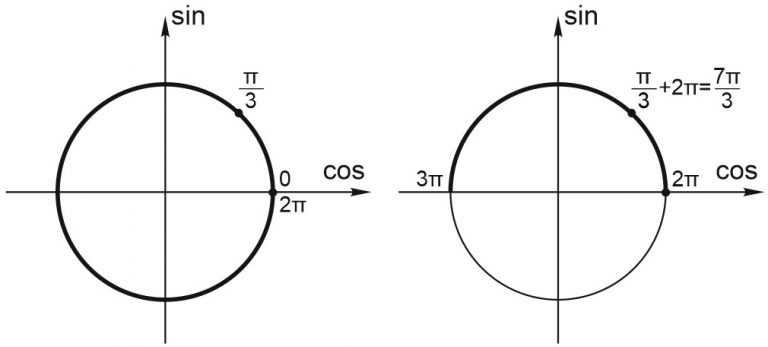
Видим, что данному отрезку принадлежат точки: \(\displaystyle x_{1}=\frac{\pi }{3}; \; x_{2}=2\pi +\frac{\pi }{3}=\frac{7\pi }{3}.\)
Ответ: а) \(\displaystyle \frac{\pi }{3}+2\pi n, \; n\in Z.\)
б) \(\displaystyle \frac{\pi }{3}; \; \frac{7\pi }{3}.\)
Другой пример.
10. а) Решите уравнение: \(cosx+sinx=1.\)
б) Найдите все корни уравнения на отрезке \([0; \pi ].\)
Решение:
Делим обе части на \(\sqrt{2}:\)
\(\displaystyle \frac{1}{\sqrt{2}}cosx+\frac{1}{\sqrt{2}}sinx=\frac{1}{\sqrt{2}}.\)
Сделаем теперь для разнообразия в левой части косинус разности:
\(\displaystyle cos\frac{\pi }{4}cosx+sin\frac{\pi }{4}sinx=\frac{1}{\sqrt{2}};\)
\(\displaystyle cos\left ( x-\frac{\pi }{4} \right )=\frac{1}{\sqrt{2}};\)
\(\displaystyle x-\frac{\pi }{4}=\pm \frac{\pi }{4}+2\pi n, \; n\in Z;\)
\(\displaystyle x_{1}=\frac{\pi }{2}+2\pi n; \; x_{2}=2\pi n, \; n\in Z.\)
б) Найдем корни уравнения, принадлежащие отрезку \([0; \pi ]\) с помощью единичной окружности. Отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежат точки \(0\) и \(\displaystyle \frac{\pi }{2}.\)
Ответ: а) \(\displaystyle \frac{\pi }{2}+2\pi n; \; 2\pi n, \; n\in Z.\)
б) \(0;\) \(\displaystyle \frac{\pi }{2}.\)
Покажем, как применяется метод введения дополнительного угла в общем случае.
Рассмотрим уравнение \(acosx+bsinx=c.\)
Делим обе части на \(\sqrt{a^{2}+b^{2}}:\)
|
\( \displaystyle \frac{a}{\sqrt{a^{2}+b^{2}}}cosx+\frac{b}{\sqrt{a^{2}+b^{2}}}sinx=\frac{c}{\sqrt{a^{2}+b^{2}}}.\) |
(4) |
Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:
\( \displaystyle \left ( \frac{a}{\sqrt{a^{2}+b^{2}}} \right )^{2}+\left ( \frac{b}{\sqrt{a^{2}+b^{2}}} \right )^{2}=1.\)
Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла \(\alpha \):
\( \displaystyle \frac{a}{\sqrt{a^{2}+b^{2}}}=cos\alpha , \; \frac{b}{\sqrt{a^{2}+b^{2}}}=sin\alpha.\)
Соотношение (4) тогда приобретает вид:
\( \displaystyle cos\alpha cosx+sin\alpha sinx=\frac{c}{\sqrt{a^{2}+b^{2}}}\) или \(\displaystyle cos(x-\alpha )=\frac{c}{\sqrt{a^{2}+b^{2}}}.\)
Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол \(\alpha .\)
к оглавлению ▴
Универсальная подстановка
Запомним две важные формулы:
\(\displaystyle sinx=\frac{2tg\frac{x}{2}}{1+tg^{2}\frac{x}{2}}, \; cosx=\frac{1-tg^{2}\frac{x}{2}}{1+tg^{2}\frac{x}{2}}.\)
Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной тригонометрической подстановки.
Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при \(x=\pi +2\pi n, \; n\in Z\). Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
11. а) Решите уравнение: \(sin2x+tgx=2.\)
б) Найдите все корни уравнения на отрезке \([0; \pi ].\)
Решение:
Выражаем \(sin2x\), используя универсальную тригонометрическую подстановку:
\(\displaystyle \frac{2tgx}{1+tg^{2}x}+tgx=2.\)
Делаем замену: \(t=tgx.\)
\(\displaystyle \frac{2t}{1+t^{2}}+t=2.\)
Получаем кубическое уравнение:
\(t^{3}-2t^{2}+3t-2=0;\)
\((t-1)(t^{2}-t+2)=0.\)
Оно имеет единственный корень \(t=1.\)
Стало быть, \(tgx=1\), откуда \(x=\displaystyle \frac{\pi }{4}+\pi n, \; n\in Z.\)
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало \(tgx.\)
б) Найдем корни уравнения, принадлежащие отрезку \([0; \pi ],\) с помощью двойного неравенства:
\(\displaystyle 0\leq \displaystyle \frac{\pi }{4}+\pi n\leq \pi , \; n\in Z;\)
\(\displaystyle -\frac{1}{4}\leq n\leq \frac{3}{4}.\)
Получим, что \(\displaystyle n=0; \; x=\frac{\pi }{4}.\)
Ответ: а) \(\displaystyle \frac{\pi }{4}+\pi n, \; n\in Z.\)
б) \(\displaystyle \frac{\pi }{4}.\)
Универсальная тригонометрическая подстановка может также пригодиться при решении задач по планиметрии из второй части ЕГЭ. Поэтому формулы лучше выучить.
к оглавлению ▴
Учет ОДЗ уравнения
12. а) Рассмотрим уравнение: \(\sqrt{5cosx-cos2x}+2sinx=0.\)
б) Найдите все корни уравнения на отрезке \(\displaystyle \left [ -\frac{\pi }{2}; \frac{3\pi }{2} \right ].\)
Решение:
Перепишем уравнение в виде, пригодном для возведения в квадрат:
\(\sqrt{5cosx-cos2x}=-2sinx.\)
Тогда наше уравнение равносильно системе:
\(\left\{\begin{matrix}
5cosx-cos2x=4sin^{2}x, \\ sinx\leq 0.
\end{matrix}\right.\)
Решаем уравнение системы:
\(5cosx-(2cos^{2}x-1)=4(1-cos^{2}x);\)
\(2cos^{2}x+5cosx-3=0;\)
\(\left[\begin{matrix}
\displaystyle cosx=\frac{1}{2}, \\cosx=-3.
\end{matrix}\right.\)
Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:
\(x_{1}=\displaystyle \frac{\pi }{3}+2\pi n; \; x_{2}=-\frac{\pi }{3}+2\pi n, \; n\in Z.\)
Теперь нужно произвести отбор решений в соответствии с неравенством \(sinx\leq 0\). Серия \(x_{1}\) не удовлетворяет этому неравенству, а серия \(x_{2}\) удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия \(x_{2}\).
Ответ в пункте (а): \(x=\displaystyle -\frac{\pi }{3}+2\pi n, \; n\in Z.\)
б) Найдем корни уравнения, принадлежащие отрезку \(\displaystyle \left [ -\frac{\pi }{2}; \frac{3\pi }{2} \right ],\) с помощью двойного неравенства:
\(\displaystyle \frac{-\pi }{2}\leq -\frac{\pi }{3}+2\pi n\leq \frac{3\pi }{2};\)
\(\displaystyle -\frac{1}{12}\leq n\leq \frac{11}{12}.\)
Неравенство имеет единственное целое решение \(n=0.\)
Тогда \(\displaystyle x=-\frac{\pi }{3}.\)
Ответ: а) \(\displaystyle -\frac{\pi }{3}+2\pi n, \; n\in Z.\)
б) \(\displaystyle -\frac{\pi }{3}.\)
Мы рассмотрели основные методы решения тригонометрических уравнений, которые применяются в задаче 13 ЕГЭ.
Где же еще нам могут встретиться тригонометрические уравнения? Конечно, в задачах с параметрами. Или на олимпиадах по математике. Сейчас мы увидим еще несколько полезных приемов решения.
к оглавлению ▴
Метод оценки
В некоторых уравнениях на помощь приходят оценки \(-1\leq sinx\leq1, \; -1\leq cosx\leq1.\)
13. Рассмотрим уравнение: \(sin5x+sin9x=2.\)
Решение:
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в том случае, когда они равны единице одновременно:
\(\left\{\begin{matrix}
sin5x=1, \\sin9x=1.
\end{matrix}\right. \)
Таким образом, должны одновременно выполняться следующие равенства:
\(\left\{\begin{matrix}
\displaystyle 5x=\frac{\pi }{2}+2\pi n, \\\displaystyle 9x=\frac{\pi }{2}+2\pi k;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
\displaystyle x=\frac{\pi }{10}+\frac{2\pi n}{5}, \\\displaystyle x=\frac{\pi }{18}+\frac{2\pi k}{9},
\end{matrix}\right. \; n,\;k\in Z.\)
Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения \(x\) удовлетворяют обоим равенствам. Имеем:
\(\displaystyle \frac{\pi }{10}+\frac{2\pi n}{5}=\frac{\pi }{18}+\frac{2\pi k}{9}.\)
Умножаем обе части на \(90\) и сокращаем на \(\pi \):
\(9+36n=5+20k;\)
\(20k=36n+4;\)
\(5k=9n+1. \)
Правая часть, как видим, должна делиться на \(5\). Число \(n\) при делении на \(5\) может давать остатки от \(0\) до \(4\); иначе говоря, число \(n\) может иметь один из следующих пяти видов: \(5n, \; 5m+1, \; 5m+2, \; 5m+3\) и \(5m+4\), где \(m\in Z\). Для того, чтобы \(9n+ 1\) делилось на \(5\), годится лишь \(n=5m+1.\)
Искать \(k\), в принципе, уже не нужно. Сразу находим \(x\):
\(x=\displaystyle \frac{\pi }{10}+\frac{2\pi n}{5}=\frac{\pi }{10}+\frac{2\pi (5m+1)}{5}+2\pi m.\)
Ответ: \(x=\displaystyle \frac{\pi }{2}+2\pi m, \; m\in Z.\)
14. Рассмотрим уравнение: \(sin2xsin5x=1.\)
Решение:
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны \(1\) или \(-1.\) Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.
Лучше поступить по-другому: умножим обе части на \(2\) и преобразуем левую часть в разность косинусов:
\(2sin2xsin5x=2;\)
\(cos3x-cos7x=2.\)
Тем самым мы сокращаем работу вдвое, получая лишь одну систему:
\(\left\{\begin{matrix}
cos3x=1, \\ cos7x=-1.
\end{matrix}\right.\)
Имеем:
\(\left\{\begin{matrix}
3x=2\pi n, \\ 7x=\pi +2\pi k;
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
\displaystyle x=\frac{2\pi n}{3}, \\ \displaystyle x=\frac{\pi }{7}+\frac{2\pi k}{7},
\end{matrix}\right. \; n, \; k \in Z.\)
Ищем пересечение:
\(\displaystyle \frac{2\pi n}{3}=\frac{\pi }{7}+\frac{2\pi k}{7}.\)
Умножаем на \(21\) и сокращаем на \(\pi \):
\(14n=3+6k.\)
Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.
Это был тренировочный пример. А в задачах ЕГЭ решения есть всегда.
Посмотрите, как применяется метод оценки в задачах с параметрами.
15. Страшное с виду уравнение \(sin^{5}x+cos^{8}x=1\) также решается методом оценок.
Решение:
В самом деле, из неравенства \(\left|sinx \right|\leq 1, \; \left|cosx \right|\leq 1\), следует, что \(sin^{5}x\leq sin^{2}x, \; cos^{8}x\leq cos^{2}x.\)
Следовательно, \(sin^{5}x+cos^{8}x\leq sin^{2}x+cos^{2}x=1\), причём равенство возможно в том и только в том случае, когда
\(\left\{\begin{matrix}
sin^{5}x=sin^{2}x,\\
cos^{8}x=cos^{2}x.\\
\end{matrix}\right. \)
Остаётся решить полученную систему. Это не сложно.
Перенесем в левую часть и вынесем общий множитель за скобки, получим:
\(\left\{\begin{matrix}
sin^{2}x(sin^{3}x-1)=0, \\
cos^{2}x(cos^{6}x-1)=0. \\
\end{matrix}\right. \)
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.
Каждое уравнение равносильно совокупности:
\(\left\{\begin{matrix}
\left[\begin{array}{c}
sinx=0,\\
sinx=1,\\
\end{array}\right. \\
\left[\begin{array}{c}
cosx=0,\\
cosx=1,\\
cosx=-1.\\
\end{array}\right. \\
\end{matrix}\right.\)
Это значит, что синус угла \(x\) равен нулю, а его косинус равен \(0\), \(1\) или \(-1\).
Или синус угла \(x\) равен \(1\), а косинус этого угла равен \(0\), \(1\) или \(-1\).
Такие углы легко найти на тригонометрическом круге. Найденные серии решений запишем в ответ.
Ответ: \(\displaystyle 2\pi n; \; \frac{\pi }{2}+2\pi n; \; \pi +2\pi n, \; n\in Z.\)
к оглавлению ▴
Тригонометрические уравнения повышенной сложности.
Приемы решения
16. Рассмотрим такое уравнение: \(sin2x=cosx+sinx+1.\)
Решение:
Сделаем замену \(t=cosx+sinx.\)
Как выразить \(sin2x\) через \(t\)? Имеем:
\(t^{2}=cos^{2}x+2cosxsinx+sin^{2}x=1+sin2x\), откуда \(sin2x=t^{2}-1.\)
Получаем:
\(t^{2}-1=t+1;\)
\(t^{2}-t-2=0;\)
\(t_{1}=-1; \; t_{2}=2.\)
\(\left[\begin{array}{c}
cosx+sinx=-1,\\
cosx+sinx=2.\\
\end{array}\right.\)
Начнем со второго уравнения.
Так как \(-1\leq sinx\leq 1\) и \(-1\leq cosx\leq 1,\) то их сумма может быть равна \(2\), только оба слагаемых равны \(1\). Но на единичной окружности не существует точки, в которой одновременно синус и косинус равен единице. Значит, второе уравнение корней не имеет.
Решим первое уравнение методом введения дополнительного угла.
Для этого разделим обе части уравнения на \(\sqrt{2}\) и получим:
\(\displaystyle cosx+sinx=-1\Leftrightarrow \frac{1}{\sqrt{2}}cosx+\frac{1}{\sqrt{2}}sinx=-\frac{1}{\sqrt{2}}\Leftrightarrow\)
\(\displaystyle \Leftrightarrow cosx\cdot cos\frac{\pi }{4}+sinx\cdot sin\frac{\pi }{4}=-\frac{1}{\sqrt{2}}\Leftrightarrow cos\left ( x+\frac{\pi }{4} \right )=-\frac{1}{\sqrt{2}}\Leftrightarrow\)
\(\displaystyle \Leftrightarrow x+\frac{\pi }{4}=\pm \frac{3\pi }{4}+2\pi k, \; k\in Z;\)
\( \left[\begin{array}{c}
\displaystyle x=\frac{\pi }{2}+2\pi k, \; k\in Z,\\
x=-\pi +2\pi k, \; k\in Z.\\
\end{array}\right.\)
Ответ: \(\displaystyle \frac{\pi }{2}+2\pi k; \; -\pi +2\pi k, \; k\in Z.\)
17. Помним формулы косинуса и синуса тройного угла:
\(cos3\alpha =4cos^{3}\alpha -3cos\alpha, \)
\(sin3\alpha = 3sin\alpha -4sin^{3}\alpha.\)
Вот, например, уравнение:
\(sin3x+2cos2x=2.\)
Оно сводится к уравнению относительно \(sinx\):
\(3sinx-4sin^{3}x+2(1-2sin^{2}x)=2;\)
\(4sin^{3}x+4sin^{2}x-3sinx=0;\)
\(sinx(4sin^{2}x+4sinx-3)=0. \)
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:
\(\left[\begin{array}{c}
sinx=0,\\
4sin^{2}x+4sinx-3=0.\\
\end{array}\right. \)
Решим второе уравнение с помощью замены \(sinx = t\).
Получим: \(\displaystyle 4t^{2}+4t-3=0; \; D=16+48=64; \; t=-\frac{3}{2}\) или \(\displaystyle t=\frac{1}{2}.\)
Обратная замена:
\(\left[\begin{array}{c}
\displaystyle sinx=-\frac{3}{2},\\
\displaystyle sinx=\frac{1}{2};\\
\end{array}\right. \Leftrightarrow \left[\begin{array}{c}
x\in \varnothing, \\
\displaystyle x=\frac{\pi }{6}+2\pi n, \; n\in Z,\\
\displaystyle x=\frac{5\pi }{6}+2\pi n, \; n\in Z.\\
\end{array}\right.\)
А решением первого уравнения \(sinx = 0\) являются числа вида \(x=\pi k, \; k\in Z.\)
Ответ: \(\displaystyle \pi k, \; k\in Z; \; \frac{\pi }{6}+2\pi n; \; \frac{5\pi }{6}+2\pi n, \; n\in Z.\)
Интересно, что формулы синуса и косинуса тройного угла также могут пригодиться вам в решении задач по планиметрии из второй части ЕГЭ.
18. Как бороться с суммой четвёртых степеней синуса и косинуса?
Рассмотрим уравнение: \(sin^{4}x+cos^{4}x=\displaystyle \frac{5}{8}.\)
Решение:
Выделяем полный квадрат:
\(\displaystyle sin^{4}x+cos^{4}x+2sin^{2}xcos^{2}x-2sin^{2}xcos^{2}x=\frac{5}{8};\)
\(\displaystyle (sin^{2}x+cos^{2}x)^{2}-2sin^{2}xcos^{2}x=\frac{5}{8};\)
\(\displaystyle 1-\frac{1}{2}sin^{2}2x=\frac{5}{8};\)
\(\displaystyle sin^{2}2x=\frac{3}{4};\)
\(\displaystyle sin2x=\pm \frac{\sqrt{3}}{2};\)
\(\displaystyle 2x=\pm \frac{\pi }{3}+\pi n;\)
\(\displaystyle x=\pm \frac{\pi }{6}+\frac{\pi n}{2}, \; n\in Z.\)
19. А как быть с суммой шестых степеней?
Рассмотрим такое уравнение: \(sin^{6}x+cos^{6}x=\displaystyle \frac{1}{4}.\)
Решение:
Раскладываем левую часть на множители как сумму кубов: \(a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2}).\)
Получим:
\((sin^{2}x+cos^{2}x)(sin^{4}x-sin^{2}xcos^{2}x+cos^{4}x)=\displaystyle \frac{1}{4};\)
\(sin^{4}x-sin^{2}xcos^{2}x+cos^{4}x=\displaystyle \frac{1}{4}. \)
С суммой четвёртых степеней вы уже умеете обращаться.
Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.
В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.